
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
G 3.10 Приклад розв’язку індивідуального завдання 6 ⇐ ПредыдущаяСтр 6 из 6
У півсмузі
Перетворимо неоднорідні граничні умови (3.10.2) на однорідні. Розв’язок задачі (3.10.1) — (3.10.3) представимо у вигляді суми:
де одна з функцій, наприклад,
Представимо функцію
тоді
Використовуючи умови (3.10.5):
Складемо крайову задачу для визначення функції
На підставі (3.10.6) знаходимо:
Оскільки диференціальне рівняння (3.10.8) і граничні умови (3.10.9) однорідні, то для розв’язку отриманої крайової задачі (3.10.8) — (3.10.10) застосовуємо метод Фур'є. Розв’язок даної задачі відповідає розв’язку задачі
Визначаємо
тоді, при
Підставляючи визначені значення констант (3.10.12), (3.10.13) у розкладання (3.10.11), одержуємо:
приймаючи в останньому виразі
? 3.11 Варіанти індивідуального завдання 6
У півсмузі
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20. ? 3.12 Варіанти індивідуального завдання 7 Шляхом перетворення неоднорідних граничних умов на однорідні, розв’язати крайову задачу для рівняння гіперболічного типу
? 3.13 Варіанти індивідуального завдання 8 Розв’язати крайову задачу:
Термінологічний словник
Символи позначень похідних
Рекомендована література Основна: 1. Мартинсон Л.К. Дифференциальные уравнения математической физики / Л.К.Мартинсон, Ю.И.Малов. – М: МГТУ им. Н.Э. Баумана, 2002. – 367с.
2. Кошляков Н.С. Основные дифференциальные уравнения математической физики / Кошляков Н.С., Глинер Э.Б., Смирнов М.М. - М.: Наука, 1962.- 262с.
Додаткова: 1. Араманович И.Г. Уравнения математической физики / И.Г.Араманович, В.И.Левин. - М.: Наука, 1964. - 286с.
2. Левин В.И. Дифференциальные уравнения математической физики / В.И.Левин, Ю.И.Гроссберг. - М.: Наука, 1951.- 247с.
3. Тихонов А.Н. Уравнения математической физики / А.Н.Тихонов, А.А.Самарский. - М.: Наука, 1953.- 348с.
4. Тихонов А.Н. Методы решения некорректных задач / А.Н.Тихонов, В.Я. Арсенин. - М.: Наука, 1979.- 374с. Навчально-методичне видання
Костюшко Ірина Анатоліївна, Швидка Світлана Петрівна
|
|||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 251; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.125.219 (0.035 с.) |
 ,
,  розв’язати задачу:
розв’язати задачу: ; (3.10.1)
; (3.10.1) ; (3.10.2)
; (3.10.2) . (3.10.3)
. (3.10.3) , (3.10.4)
, (3.10.4)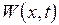 , задовольняє граничні умови:
, задовольняє граничні умови: . (3.10.5)
. (3.10.5) ,
, .
.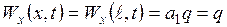 , укладаємо
, укладаємо  . Вважаючи
. Вважаючи  , отримуємо:
, отримуємо: . (3.10.6)
. (3.10.6) . Для цього підставимо вираз (3.10.4) у задачу (3.10.1) — (3.10.3):
. Для цього підставимо вираз (3.10.4) у задачу (3.10.1) — (3.10.3): (3.10.7)
(3.10.7) ,
,  ; тому на підставі крайових умов (3.10.5), відповідно до (3.10.7) для функції
; тому на підставі крайових умов (3.10.5), відповідно до (3.10.7) для функції  , (3.10.8)
, (3.10.8) 
 , (3.10.9)
, (3.10.9) . (3.10.10)
. (3.10.10) , розглянутої у темі 2 і має вигляд
, розглянутої у темі 2 і має вигляд . (3.10.11)
. (3.10.11)

 згідно з початковою умовою (3.10.10):
згідно з початковою умовою (3.10.10):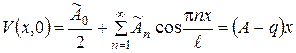 ,
,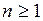
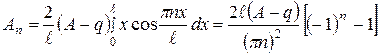 (3.10.12)
(3.10.12) . (3.10.13)
. (3.10.13) ,
, і підставляючи отриманий вираз у співвідношення (3.10.4) з урахуванням (3.10.6), одержуємо остаточний розв’язок крайової задачі (3.10.1)-(3.10.3) у вигляді:
і підставляючи отриманий вираз у співвідношення (3.10.4) з урахуванням (3.10.6), одержуємо остаточний розв’язок крайової задачі (3.10.1)-(3.10.3) у вигляді: .
. .
. .
. .
. .
. .
. .
. .
.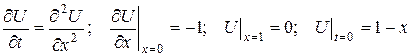 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.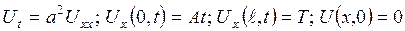 .
. .
. .
.






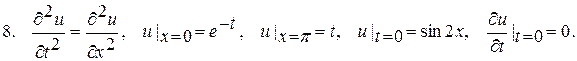


































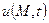 - шукана функція, розв’язок рівняння (задачі) математичної фізики
- шукана функція, розв’язок рівняння (задачі) математичної фізики - норма функції
- норма функції 
 - Декартові координати
- Декартові координати - радіальна координата
- радіальна координата - тимчасова змінна
- тимчасова змінна - похідні функції
- похідні функції 
 - частинні похідні функції
- частинні похідні функції 
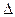 - оператор Лапласа
- оператор Лапласа - двовимірний оператор Лапласа
- двовимірний оператор Лапласа


