
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
У частинних похідних другого порядкуСтр 1 из 6Следующая ⇒
Велика кількість різних фізичних задач приводить до диференціальних рівнянь із частинними похідними, які являють собою співвідношення між невідомою функцією
Якщо диференціальне рівняння лінійне відносно старших похідних, то його називають квазілінійним рівнянням та записують у вигляді
де Диференціальне рівняння називають лінійним, якщо воно лінійне як відносно шуканої функції, так і відносно її частинних похідних. Таке рівняння записують у вигляді
Якщо коефіцієнти рівняння (1.1.3) не залежать від змінних Рівнянням (1.1.2) та (1.1.3) можна поставити у відповідність квадратичну форму
та за аналогією до з кривих другого порядку дати класифікацію типів рівнянь за знаком дискримінанта. Виділимо три типи рівнянь у формі (1.1.2) або (1.1.3), називаючи їх рівняннями гіперболічного типу, якщо в деякій точці В рівнянні (1.1.2) можна зробити заміну незалежних змінних
з якобіаном перетворення
який допускає звернене перетворення. Тоді в нових змінних рівняння (1.1.2) набуває вигляду
Тут
Перетворення (1.1.4) не змінює тип рівняння, тому що Перехід до канонічної форми можна здійснити за допомогою загальних інтегралів диференціального рівняння
яке називають характеристичним для рівняння (1.1.2) та (1.1.3), а його інтеграли – характеристичними кривими, або характеристиками. Якщо
Якщо в деякій області
де приходимо до рівняння (1.1.5), в якому згідно з (1.1.7)
Якщо в деякій області
Якщо в деякій області
Лінійне рівняння зі сталими коефіцієнтами (1.1.3) мають однаковий тип у будь - якій області
Якщо тепер ввести нову невідому функцію
де то за допомогою підбору цих сталих канонічні форми для рівнянь зі сталими коефіцієнтами можна привести до спрощеного вигляду
для рівнянь гіперболічного, параболічного та еліптичного типів відповідно.
|
|||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 337; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.63.87 (0.008 с.) |
 , її частинними похідними та незалежними змінними. Найчастіше в математичній фізиці зустрічаються диференціальні рівняння другого порядку. Для двох незалежних змінних
, її частинними похідними та незалежними змінними. Найчастіше в математичній фізиці зустрічаються диференціальні рівняння другого порядку. Для двох незалежних змінних  таке диференціальне рівняння записують у загальній формі співвідношенням
таке диференціальне рівняння записують у загальній формі співвідношенням . (1.1.1)
. (1.1.1)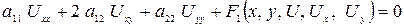 , (1.1.2)
, (1.1.2) — деякі функції незалежних змінних.
— деякі функції незалежних змінних. (1.1.3)
(1.1.3) , то воно являє собою лінійне диференціальне рівняння зі сталими коефіцієнтами.
, то воно являє собою лінійне диференціальне рівняння зі сталими коефіцієнтами.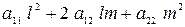
 (або області
(або області  )
)  , параболічного типу, — якщо в деякій точці
, параболічного типу, — якщо в деякій точці  , і еліптичного типу, - якщо у точці
, і еліптичного типу, - якщо у точці  . Тут
. Тут  — дискримінант рівняння.
— дискримінант рівняння. (1.1.4)
(1.1.4)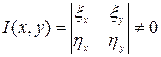 ,
, . (1.1.5)
. (1.1.5)


 . Однак функції
. Однак функції  та
та  можна вибрати таким чином, щоб у нових змінних частина коефіцієнтів обернулася в нуль, а саме рівняння (1.1.5) набуло простішого вигляду, який називають канонічною формою рівняння.
можна вибрати таким чином, щоб у нових змінних частина коефіцієнтів обернулася в нуль, а саме рівняння (1.1.5) набуло простішого вигляду, який називають канонічною формою рівняння. , (1.1.6)
, (1.1.6) — загальний інтеграл рівняння (1.1.6), то функція
— загальний інтеграл рівняння (1.1.6), то функція  є розв’язком диференціального рівняння першого порядку
є розв’язком диференціального рівняння першого порядку . (1.1.7)
. (1.1.7)
 — рівняння характеристик,
— рівняння характеристик, . Отриманий вираз ділимо на
. Отриманий вираз ділимо на  , приводимо рівняння (1.1.5) до канонічної форми для рівняння гіперболічного типу:
, приводимо рівняння (1.1.5) до канонічної форми для рівняння гіперболічного типу: . (1.1.8)
. (1.1.8) . Покладемо
. Покладемо  та
та  , де
, де  — довільна, лінійно незалежна з
— довільна, лінійно незалежна з  функція, приходимо до перетвореного рівняння (1.1.5), в якому згідно (1.1.7) та умови параболічності
функція, приходимо до перетвореного рівняння (1.1.5), в якому згідно (1.1.7) та умови параболічності  . Таким чином, отримуємо наступну канонічну форму для рівняння параболічного типу
. Таким чином, отримуємо наступну канонічну форму для рівняння параболічного типу . (1.1.9)
. (1.1.9) , де
, де  . Поклавши
. Поклавши  . Тому після перетворення рівняння (1.1.5) можна записати в канонічному вигляді для еліптичного рівняння:
. Тому після перетворення рівняння (1.1.5) можна записати в канонічному вигляді для еліптичного рівняння: . (1.110)
. (1.110) ;
; ;
; .
. за правилом
за правилом ,
, — деякі сталі,
— деякі сталі, ;
; ;
;



