
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Диаграмма Хассе частично упорядоченного множестваСодержание книги
Поиск на нашем сайте
Напомним, что ориентированным графом называется пара (V,A), состоящая из множества V и подмножества AÍV´V. Элементы из A называются стрелками, а из V – вершинами. Для стрелки (u,v) вершина u называется началом, а из v – концом. Пусть (X,£) – частично упорядоченное множество. Множество ]x,y[ = {vÎX: x<v<y} называется открытым интервалом с концами x и y. Определение 1. Диаграммой Хассе называется ориентированный граф (V,A) с V=X и A ={ (u,v): u<v и ]u,v[ = Æ }. Пример 1. На рис. 5.1 показана диаграмма Хассе множества P({0,1,2}) подмножеств множества {0,1,2}, упорядоченное отношением Í.
Рис. 5.1. Диаграмма Хассе множества подмножеств Предполагаются, что ребра направлены сверху вниз. Пример 2. Для целого неотрицательного числа n³0 будем обозначать через [n] множество {0, 1, ∙ ∙ ∙, n}, с отношением 0 < 1< ∙ ∙ ∙ < n. Его диаграммой Хассе будет ориентированный граф, приведенный на рис. 5.2.
·®·®·® × × × ®·®· Рис. 5.2. Диаграмма Хассе
Частично упорядоченные множества (X, £) и (Y, £) называются изоморфными, если существуют неубывающие отображения f: X®Y и g: Y®X такие, что f(g(y))=y и g(f(x))=x ("xÎX, "yÎY). В этом случае f называется изоморфизмом, а g – обратным отображением для f. Рассмотрим множество делителей (Dn, |) натурального числа n³1, упорядоченное отношением делимости a | b Û a – делитель числа b (в этом случае говорят, что a – делит b). Пример 3. Пусть p и q – различные простые числа, большие единицы. Диаграмма Хассе множества (Dn, |) с n=p2q показана на рисунке 5.3.
Рис. 5.3. Диаграмма Хассе множества делителей В общем случае диаграмма Хассе частично упорядоченного множества (Dn,|) состоит из ребер m -мерного параллелепипеда, где m – число различных простых делителей числа n. Теорема 1. Пусть n>0 – положительное натуральное число, n = Доказательство. Каждый делитель числа n = Функция Мебиуса Пусть (X, £) – конечное частично упорядоченное множество. Рассмотрим последовательность функций Pn: X´X® Z, определенных при n =0 и n =1 по формулам:
А при n≥2: Pn(x,y) = |{(x1 , x2 , ×× ×, xn-1): x< x1 < x2 < ××× < xn-1 <y}|. Определение 1. Функцией Мебиуса m: X´X®Z называется функция, определенная по формуле
Определение 2. Пусть X={ x1 , x2 , ×××, xn} – конечное частично упорядоченное множество, матрицей смежности называется матрица A, имеющая коэффициенты
Лемма 1. Пусть X={ x1 , x2 , ×××, xn} – конечное частично упорядоченное множество, A – матрица смежности. Тогда матрица M, коэффициенты которой равны значениям m(xi, xj), будет обратной к матрице A. Доказательство. Пусть Id – единичная матрица. Положим Q=A-Id. Тогда A=Id+Q. Откуда A-1 = Id - Q + Q2 - Q3 + ××× = Легко видеть, что коэффициенты матрицы Qk равны Pk(xi,xj), откуда Пример 1. X=[n].
Отсюда получаем m(i,i)=1, m(i,i+1)=-1. Остальные значения функции Мебиуса равны 0. Формула обращения Теорема 1. Пусть (X, £) – конечное частично упорядоченное множество. Тогда для любых функций f, g: X® R равносильны следующие свойства (1) (2) Доказательство. Пусть A – матрица смежности частично упорядоченного множества (X, £). Тогда выполнение равенства (1) равносильно соотношениям g(xi)=Sj aij f(xj). Поскольку это равносильно равенству g=Af, эквивалентного равенству f=A-1g, то получаем, что (1) верно тогда и только тогда, когда верно (2). Рассматривая частично упорядоченное множество с двойственным отношением порядка, получаем следующую теорему. Теорема 2. Пусть (X, £) – конечное частично упорядоченное множество. Тогда для любых функций f, g: X® R равносильны следующие свойства (1) (2)
Теорема о произведении Теорема 1. Пусть (X,£) и (Y,£) – конечные частично упорядоченные множества, mX: X´X® Z и mY: Y´Y® Z – их функции Мебиуса. Тогда, для любых x1, x2 Î X и y1, y2 Î Y имеет место равенство mX´Y ((x1, y1), (x2 , y2 )) = mX (x1, x2) mY (y1, y2). Доказательство. Введем дзета-функцию zX: X´X® Z, с помощью формулы zX (x1, x2 ) = 1 Û x1 £ x2. Достаточно доказать формулу
где da,b – символ Кронекера. Вычислим левую часть доказываемой формулы
Получили, что она равна правой части. Что и требовалось доказать. Пример 1. Вычислим
то имеем m(1,n) = 0, если существует i такой, что ai >1, m(1,n) =(-1)m, если n = p1p2 × × × pm. Упражнения Диаграмма Хассе 1. Нарисовать диаграмму Хассе множества подмножеств из {0,1,2,3}, упорядоченное отношением включения. 2. Нарисовать диаграмму Хассе множества делителей числа 1000, упорядоченного отношением делимости. 3. Нарисовать диаграмму Хассе множества делителей числа 360, упорядоченного отношением делимости. 4. Нарисовать диаграмму Хассе множества P3 разбиений множества {1,2,3}. 5. Нарисовать диаграмму Хассе множества P4 разбиений множества {1,2,3,4}. 6. Нарисовать диаграмму Хассе произведения P3 ´[1]. Функция Мебиуса 1. Вычислить значения m(0, x) непосредственно из определения функции Мебиуса для следующих частично упорядоченных множеств, заданных с помощью диаграмм Хассе, приведенных на рис. 5.4.
Рис. 5.4. Примеры диаграмм Хассе 2. Вычислить значения функции Мебиуса для множества P({1,2, ×××, n}), упорядоченного отношением Í. 3. Пусть a – произвольный элемент частично упорядоченного множества. Доказать, что
РАСЧЕТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ Задача 1. Найти множество X, предполагая множества A, B и C известными. Предполагается, что все множества являются подмножествами некоторого универсума U. При каких условиях заданное уравнение обладает по крайней мере одним решением?
Варианты заданий
Пример решения задачи 1 Задача. Найти множество X, удовлетворяющее уравнению Решение. 1 шаг. Уравнение равносильно следующему равенству
Пользуясь формулой
С помощью правил де Моргана
2 шаг. Обозначим операцию объединения Èзнаком сложения, а операцию пересечения Ç - знаком умножения. Получим уравнение
Преобразуем его с помощью закона дистрибутивности (P+Q)R=PR+QR. Приходим к уравнению
Равенства
3 шаг. Полученное уравнение равносильно системе двух уравнений
Из первого уравнения получаем Ответ: Задача 2. Задано отношение R на множестве E = {1, 2, 3, 4, 5} с помощью матрицы rij, где
Представить данное отношение с помощью ориентированного графа, вершинами которого являются элементы множества E. Вершины i и j соединяются стрелкой, если Выписать матрицы, соответствующие отношениям 1) R-1 , 2) RºR, 3) RÇ R-1. Является ли это отношение R 1) рефлексивным, 2) иррефлексивным, 3) симметричным, 4) антисимметричным, 5) транзитивным, 6) отношением порядка, 7) отношением эквивалентности. Варианты заданий
Пример решения задачи 2.
Задание. Выполнить действия, указанные в условии задачи 2, если отношение R на множестве E = {1, 2, 3, 4, 5} задано с помощью матрицы
имеющей коэффициенты rij = 1 при (i,j)ÎR, и rij = 0 в других случаях.
Решение. Представим отношение с помощью ориентированного графа (рис.6.1), с множеством вершин E={1, 2, 3, 4, 5}. Вершины i и j соединяются стрелкой, если
Рис. 6.1. Ориентированный граф, соответствующий отношению R
Выпишем матрицы
R-1 =
R°R =
Ответим на вопросы.
Рефлексивность выполняется, поскольку rii=1 влечет (i,i)ÎR, для всех iÎE. Иррефлексивность не выполняется, ибо существуют iÎE, для которых (i,i)ÎR. (например i=1). Симметричность имеет место, ибо для всех i, j ÎE выполнено rij= rji. Антисимметричность не выполняется, так как (1,3)ÎR и (3,1)ÎR, но 1¹3. Транзитивность вытекает из R°R Í R. Отношение не является отношением порядка, ибо оно не антисимметрично. Отношение является отношением эквивалентности, поскольку оно рефлексивно, симметрично и транзитивно.
КОНТРОЛЬНАЯ РАБОТА Задача 1. Найти количество подмножеств.
Варианты заданий
1. Сколько подмножеств множества {1, 2,..., 1000} не содержат чисел ни кратных 6, ни кратных 4? 2. Сколько подмножеств множества {1, 2,...., 1000} содержат по крайней мере одно число кратное 5 и ни одного – кратного 7? 3. Сколько существует подмножеств множества {1, 2, 3,..., 1000} имеющих по крайней мере одно число, кратное трем или четырем. 4. Сколько подмножеств множества {1, 2,..., 1000} не содержат ни одного нечетного числа, но имеют по крайней мере одно число кратное 7? 5. Сколько подмножеств из {1,2,3, …, 300} состоят из чисел, делящихся на 4, и не содержат ни одного числа, делящегося на 3? 6. Сколько подмножеств множества {1,2,3, …, 1000} содержат по крайней мере одно число кратное 4, но ни одного кратного 7? 7. Сколько подмножеств множества {1, 2,..., 1000} не содержат чисел ни кратных 6, ни кратных 15? 8. Сколько подмножеств множества {1, 2,...., 1000} содержат по крайней мере одно число кратное 5 и ни одного – кратного 18? 9. Сколько существует подмножеств множества {1, 2, 3,..., 1000} имеющих по крайней мере одно число, кратное 15 или 21. 10. Сколько подмножеств множества {1, 2,..., 1000} не содержат ни одного нечетного числа, но имеют по крайней мере одно число кратное 21? 11. Сколько подмножеств из {1,2,3, …, 300} состоят из чисел, делящихся на 6, и не содержат ни одного числа, делящегося на 7? 12. Сколько подмножеств множества {1, 2,..., 1000} не содержат чисел ни кратных 8, ни кратных 6? 13. Сколько подмножеств множества {1, 2,...., 1000} содержат по крайней мере одно число кратное 12 и ни одного – кратного 13? 14. Сколько существует подмножеств множества {1, 2, 3,..., 1000} имеющих по крайней мере одно число, кратное 6 или 11. 15. Сколько подмножеств множества {1, 2,..., 1000} не содержат ни одного нечетного числа, но имеют по крайней мере одно число кратное 17? 16. Сколько подмножеств из {1,2,3, …, 300} состоят из чисел, делящихся на 7, и не содержат ни одного числа, делящегося на 3? 17. Сколько подмножеств множества {1, 2,..., 1000} не содержат чисел ни кратных 6, ни кратных 9? 18. Сколько подмножеств множества {1, 2,...., 1000} содержат по крайней мере одно число кратное 11 и ни одного – кратного 7? 19. Сколько существует подмножеств множества {1, 2, 3,..., 1000} имеющих по крайней мере одно число, кратное 12 или 13. 20. Сколько подмножеств множества {1, 2,..., 1000} не содержат ни одного нечетного числа, но имеют по крайней мере одно число кратное 23? 21. Сколько подмножеств из {1,2,3, …, 1000} состоят из чисел, делящихся на 7, и не содержат ни одного числа, делящегося на 12? 22. Сколько подмножеств множества {1, 2,..., 1000} не содержат чисел ни кратных 6, ни кратных 10? 23. Сколько подмножеств множества {1, 2,...., 1000} содержат по крайней мере одно число кратное 12 и ни одного – кратного 7? 24. Сколько существует подмножеств множества {1, 2, 3,..., 1000} имеющих по крайней мере одно число, кратное 11 или четырем. 25. Сколько подмножеств множества {1, 2,..., 1000} не содержат ни одного нечетного числа, но имеют по крайней мере одно число кратное 11? 26. Сколько подмножеств из {1,2,3, …, 300} состоят из чисел, делящихся на 2, и не содержат ни одного числа, делящегося на 3? 27. Сколько подмножеств множества {1, 2,..., 1000} не содержат чисел ни кратных 10, ни кратных 4? 28. Сколько подмножеств множества {1, 2,...., 1000} содержат по крайней мере одно число кратное 4 и ни одного – кратного 7? 29. Сколько существует подмножеств множества {1, 2, 3,..., 1000} имеющих по крайней мере одно число, кратное 3 или 8. 30. Сколько подмножеств множества {1, 2,..., 1000} не содержат ни одного нечетного числа, но имеют по крайней мере одно число кратное 5?
Примеры решения задачи 1 Пример 1. Сколько подмножеств множества A={1, 2,...., 1000} не содержат ни чисел кратных 8, ни чисел кратных 12? Решение. Для произвольного действительного числа x обозначим через [x] его целую часть. (Например [2.5]=2, [1/2]=0, [3]=3.) Пусть 12A – подмножество множества A состоящее из чисел кратных 12, A\12A Í A – подмножество чисел не кратных 12. Элементы, не кратные ни 12 ни 8, составляют множество (A\12A)\8A. Нам нужно найти число подмножеств этого множества. Поскольку число элементов этого множества равно
|(A\12A)\8A|=|A\(12AÈ8A)|=|A|-|12AÈ8A |=
|A|-|12A|-|8A |+|НОК(12,8)A|=1000-[1000/12]-[1000/8]+[1000/24],
то количество его подмножеств равно Ответ: Пример 2. Сколько подмножеств множества A={1, 2,...., 1000} содержат по крайней мере одно число кратное 8 и ни одного – кратного 12? Решение. Пусть 12A – подмножество множества A состоящее из чисел кратных 12, A\12A Í A – подмножество чисел не кратных 12. Элементы, не кратные ни 12 ни 8, составляют множество (A\12A)\8A. Каждое подмножество из A\12A может быть одного из следующих типов: 1) оно не содержит ни одного элемента кратного 8, 2) оно содержит хотя бы один элемент, кратный 8. Отсюда количество подмножеств множества A\12A равно сумме количеств подмножеств первого и второго типа. Подмножества первого типа – это в точности подмножества не содержащие ни элементов кратных 12, ни элементов, кратных 8. Нам нужно найти количество подмножеств второго типа. Следовательно, искомое число равно
Ответ: Пример 3. Сколько подмножеств множества A={1, 2,...., 1000} содержат по крайней мере одно число кратное 8 или 12? Решение. Каждое подмножество множества A обладает одним из следующих взаимоисключающих свойств: 1) оно не содержит ни чисел кратных 8, ни чисел кратных 12, 2) оно содержит по крайней мере одно число, кратное 8 или 12. Отсюда число подмножеств второго типа (которое как раз нам нужно найти) равно
Ответ:
Задача 2. Найти число разложений заданного числа в сумму слагаемых. Разложения, отличающиеся перестановкой слагаемых, считаются различными. Варианты заданий 1. Слагаемые состоят из чисел 3 и 4, сумма равна 50. 2. Слагаемые состоят из чисел 3 и 5, сумма равна 50. 3. Слагаемые состоят из чисел 2 и 5, сумма равна 50. 4. Слагаемые состоят из чисел 3 и 4, сумма равна 52. 5. Слагаемые состоят из чисел 3 и 5, сумма равна 52. 6. Слагаемые состоят из чисел 2 и 5, сумма равна 52. 7. Слагаемые состоят из чисел 3 и 4, сумма равна 54. 8. Слагаемые состоят из чисел 3 и 5, сумма равна 54. 9. Слагаемые состоят из чисел 2 и 5, сумма равна 54. 10. Слагаемые состоят из чисел 3 и 4, сумма равна 51. 11. Слагаемые состоят из чисел 3 и 5, сумма равна 51. 12. Слагаемые состоят из чисел 2 и 5, сумма равна 51. 13. Слагаемые состоят из чисел 3 и 4, сумма равна 49. 14. Слагаемые состоят из чисел 3 и 5, сумма равна 49. 15. Слагаемые состоят из чисел 2 и 5, сумма равна 49. 16. Слагаемые состоят из чисел 3 и 4, сумма равна 55. 17. Слагаемые состоят из чисел 3 и 5, сумма равна 55. 18. Слагаемые состоят из чисел 2 и 5, сумма равна 55. 19. Слагаемые состоят из чисел 3 и 4, сумма равна 46. 20. Слагаемые состоят из чисел 3 и 5, сумма равна 46. 21. Слагаемые состоят из чисел 2 и 5, сумма равна 46. 22. Слагаемые состоят из чисел 3 и 4, сумма равна 48. 23. Слагаемые состоят из чисел 3 и 5, сумма равна 48. 24. Слагаемые состоят из чисел 2 и 5, сумма равна 48. 25. Слагаемые состоят из чисел 3 и 4, сумма равна 53. 26. Слагаемые состоят из чисел 3 и 5, сумма равна 53. 27. Слагаемые состоят из чисел 2 и 5, сумма равна 53. 28. Слагаемые состоят из чисел 3 и 4, сумма равна 47. 29. Слагаемые состоят из чисел 3 и 5, сумма равна 47. 30. Слагаемые состоят из чисел 2 и 5, сумма равна 47. Пример решения задачи 2
Задание. Найти число разложений заданного числа в сумму слагаемых. Разложения, отличающиеся перестановкой слагаемых, считаются различными. Слагаемые состоят из чисел 3 и 5, сумма равна 40. Решение. Найдем сначала число слагаемых, равных 3, и число слагаемых, равных 5, дающих в сумме число 40. С этой целью решим уравнение в целых числах 3x + 5y = 40, x³0, y³0. Первое решение x=0, y=8. Чтобы найти другие решения, будем прибавлять по 5 к числу x и вычитать по 3 из числа y. Получим решения; x = 0, y=8; x = 5, y=5; x = 10, y=2; Число последовательностей чисел, состоящих из x троек и y пятерок, равно при x = 0, y=8 - при x = 5, y=5 - при x = 10, y=2 - Сумма этих чисел Ответ:
Задача 3. Перечисление функций. Для заданных m и n найти число: · функций { 1,2, …, m } ® { 1, 2, …, n }, · инъекций { 1,2, …, m } ® { 1, 2, …, n }, · сюръекций { 1,2, …, n } ® { 1, 2, …, m }, · неубывающих функций { 0,1,2, …, m } ® { 0, 1, 2, …, n }, · возрастающих функций { 0,1,2, …, m } ® { 0, 1, 2, …, n }, · неубывающих сюръекций { 0,1,2, …, n } ® { 0, 1, 2, …, m }. Варианты заданий
Пример решения задачи 3
Задание. При m =6, n =11 найти число: · функций {1,2, …, 6} ® { 1, 2, …, 11}, · инъекций {1,2, …, 6} ® { 1, 2, …, 11}, · сюръекций {1,2, …, 11} ® { 1, 2, …,6}, · неубывающих функций {0,1,2, …, 6} ® {0, 1, 2, …, 11}, · возрастающих функций {0,1,2, …, 6} ® {0, 1, 2, …, 11}, · неубывающих сюръекций {0,1,2, …, 11} ® {0, 1, 2, …,6}. Решение. Обозначим Ln = { 1,2,3, …, n }. Искомые числа вычисляются с помощью таблицы 7.1, в каждой клетке которой указано число функций Lm®Ln с заданными свойствами.
Таблица 7.1 Число функций
Возрастающие функции – это в точности неубывающие инъективные функции. Находим: · число функций {1,2,3,4,5,6 } ® { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,11} равно 116=1771561. · число инъекций {1,2,3,4,5,6 } ® { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,11 } равно · число сюръекций { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,11 } ® {1,2,3,4,5,6 } равно 6! S(11,6). Число S(11,6) вычислим с помощью значений чисел Стирлинга второго рода, приведенных в таблице 7.2. Получим 6!S(11,6) =6!179487. · число неубывающих функций {0,1,2,3,4,5,6 } ® { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,11 } равно · число возрастающих функций {0,1,2,3,4,5,6 } ® { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,11 } равно · число неубывающих сюръекций { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,11 } ® {0,1,2,3,4,5,6 } равно
Таблица 7.2 Числа Стирлинга
Задача 4. Найти производящую функцию последовательности. Варианты заданий
Пример решения задачи 4 Задание. Найти производящую функцию последовательности an = 10n/(n(n+1). Решение. Производящая функция будет равна сумме ряда Поскольку
С помощью преобразования получаем
Вычислим
Следовательно,
Ответ: Задача 5. Решить рекуррентное уравнение. Варианты заданий
Пример решения задачи 5
Задание. Решить рекуррентное уравнение un +2= un +1+12 un, u 0=1, u 1=3. Решение. Вычислим корни характеристического уравнения a2–a–12=0 с помощью формулы нахождения корней квадратного уравнения a12= |



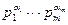 - его разложение в произведение попарно не равных простых множителей pi>1. Тогда частично упорядоченное множество (Dn, |) будет изоморфно декартовому произведению [a1]´ [a2]´ ××× ´ [am] линейно упорядоченных множеств.
- его разложение в произведение попарно не равных простых множителей pi>1. Тогда частично упорядоченное множество (Dn, |) будет изоморфно декартовому произведению [a1]´ [a2]´ ××× ´ [am] линейно упорядоченных множеств. , для некоторых 0£ b1£a1, 0£ b2£a2, × × ×, 0£ bm£am. Изоморфизм определяется как отображение, ставящее в соответствие числу
, для некоторых 0£ b1£a1, 0£ b2£a2, × × ×, 0£ bm£am. Изоморфизм определяется как отображение, ставящее в соответствие числу 

 .
.
 .
. , в силу
, в силу  . Что и требовалось доказать.
. Что и требовалось доказать. ,
,  .
. ;
; .
. ;
; .
. ,
,
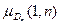 в частично упорядоченном множестве делителей числа n ≥ 1. По доказанной теореме, в случае разложения n =
в частично упорядоченном множестве делителей числа n ≥ 1. По доказанной теореме, в случае разложения n = 
 . Поскольку
. Поскольку

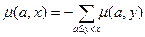 . Найти значения функций Мебиуса для задачи 1 с помощью этой формулы.
. Найти значения функций Мебиуса для задачи 1 с помощью этой формулы.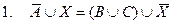















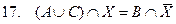













 при заданных A, B и C известными. Все множества являются подмножествами некоторого универсума U. При каких условиях заданное уравнение обладает по крайней мере одним решением?
при заданных A, B и C известными. Все множества являются подмножествами некоторого универсума U. При каких условиях заданное уравнение обладает по крайней мере одним решением? Æ.
Æ. , приходим к уравнению
, приходим к уравнению Æ
Æ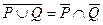 и соотношения
и соотношения  преобразуем это уравнение к следующему
преобразуем это уравнение к следующему Æ.
Æ. Æ
Æ Æ
Æ и XX = X, вместе с соотношениями
и XX = X, вместе с соотношениями 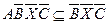 ,
,  и
и  приводят к уравнению
приводят к уравнению Æ
Æ
 , а из второго
, а из второго 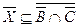 . Эти соотношения приводят к соотношениям включения
. Эти соотношения приводят к соотношениям включения  .
. .
.
 .
.


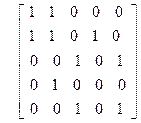
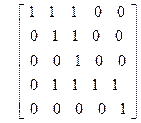

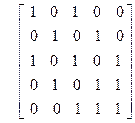
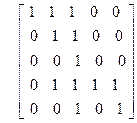



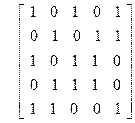

















 ,
,
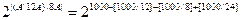
 .
.
 .
.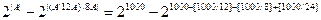
 .
. . Отсюда находим числа разложений:
. Отсюда находим числа разложений: ,
, ,
, .
.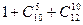 будет искомым числом разложений.
будет искомым числом разложений. .
.

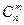
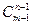
 = 332640.
= 332640. .
. .
. .
. .
. , то
, то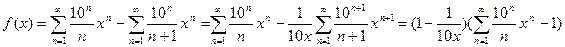 .
. ,
,
 =
= 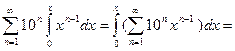
 .
. .
. .
. . Они будут равны a1 = 4, a2
. Они будут равны a1 = 4, a2


