
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема 1. Производящая функция последовательности чисел разбиенийСодержание книги
Поиск на нашем сайте
Ph(0), Ph (1), Ph (2), × × × равна Доказательство. Произведение равно (1 +x+x 2 + × × ×)(1 +x 2 +x 4 + × × ×)(1 + x 3 + x 6 + × × ×)× × ×(1 + xh + x 2 h + × × ×). Если перемножить содержимое скобок, то получим многочлен, равный сумме одночленов Следствие 1. Производящая функция последовательности чисел разбиений P(0), P(1), P(2), × × × равна Числа Фибоначчи Вычислим производящую функцию F(x) чисел Фибоначчи F0 = F1 = 1, Fn+1 = Fn + Fn-1 при n ³ 1. Т.о. числа Фибоначчи – это последовательность чисел 1, 1, 2, 3, 5... Имеют место соотношения:
Приходим к уравнению F(x)=1 + x + x2 + x(F(x)-1) для
Рекуррентные уравнения Рассмотрим обобщение последовательностей Фибоначчи. Формула un + r = c1 un + r – 1 + c2 un + r – 2 + ∙ ∙ ∙ + cr un называется однородным линейным рекуррентным уравнением порядка r. Ее решением является последовательность {un}, однозначно определенная начальными значениями u0, u1, u2, ∙ ∙ ∙, ur –1 . Решение такого уравнения называется возвратной или рекуррентной последовательностью порядка r. Пример 1. Геометрическая прогрессия является решением уравнения un+1=qun. Ее члены описываются формулой un= u0qn. Отсюда геометрическая прогрессия является возвратной последовательностью порядка 1. Пример 2. Арифметическая прогрессия un = u0 + nd удовлетворяет соотношению un+1 - un = un+2 - un+1. Получаем однородное рекуррентное уравнение un+2 = 2un+1 - un. Начальные данные задаются значениями u0 и u1=u0+d. Отсюда арифметическая прогрессия является возвратной последовательностью порядка 2. Пример 3. Произвольная периодическая последовательность является возвратной последовательностью порядка p, удовлетворяющей рекуррентному соотношению un + p=un. Здесь p – период последовательности. Для заданного рекуррентного уравнения un + r = c1 un + r – 1 + c2 un + r – 2 + ∙ ∙ ∙ + cr un найдем производящую функцию Теорема 1. Произведение u(x)K(x) = D(x) является многочленом степени меньшей, чем r. Доказательство. Вычислим коэффициент ряда D(x) при xn+ r . Он при n ≥ 0 будет равен un + r - (c1 un + r – 1 + c2 un + r – 2 + ∙ ∙ ∙ + cr un) = 0. Отсюда D(x) – многочлен степени меньшей, чем n.
|
||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 313; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.005 с.) |

 .
. . Отсюда коэффициент при xn равен числу последовательностей (l 1, l 2, × × ×, lh), для которых l 1 ×1 + l 2 ×2 + × × ×+ lh × h = n. Он будет равен числу разбиений n на слагаемые, не большие чем h.
. Отсюда коэффициент при xn равен числу последовательностей (l 1, l 2, × × ×, lh), для которых l 1 ×1 + l 2 ×2 + × × ×+ lh × h = n. Он будет равен числу разбиений n на слагаемые, не большие чем h. .
. .
.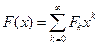 . Решая это уравнение, получаем
. Решая это уравнение, получаем 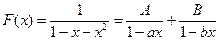 , для некоторых A, B, при
, для некоторых A, B, при  ,
, 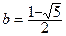 . Отсюда мы видим, что ряд F(x) равен сумме геометрических прогрессий. Находим
. Отсюда мы видим, что ряд F(x) равен сумме геометрических прогрессий. Находим  ,
,  . Следовательно,
. Следовательно,  . Отсюда получаем формулу для вычисления k –го числа Фибоначчи,
. Отсюда получаем формулу для вычисления k –го числа Фибоначчи,  , для всех k = 0, 1, 2, ∙ ∙ ∙.
, для всех k = 0, 1, 2, ∙ ∙ ∙.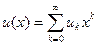 возвратной последовательности { un }. Обозначим K(x)=1- c1x - c2x2 - ∙ ∙ ∙ - crxr.
возвратной последовательности { un }. Обозначим K(x)=1- c1x - c2x2 - ∙ ∙ ∙ - crxr.


