
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Отношения порядка и эквивалентности
В данном параграфе изучаются частично упорядоченные множества и решетки. Рассматривается также отношения эквивалентности и их связь с разбиениями множества. Доказывается, что частично упорядоченное множество отношений эквивалентности на множестве является решеткой. Определение 1. Пусть X – множество. Бинарное отношение R Í X ´ X называется отношением порядка на X, если оно рефлексивно, антисимметрично и транзитивно. Таким образом, R – отношение порядка, если (1) (a,a) ÎR для всех a Î X, (2) aRb & bRa Þ a = b, (3) для всех a, b, c Î X верна импликация aRb & bRc Þ aRc, Пара (X, R), состоящая из множества X и отношения порядка R на X называется частично упорядоченным множеством. Пусть (X, R) – частично упорядоченное множество. Всякое подмножество A Í X будет частично упорядоченным множеством с отношением порядка R Ç(A ´ A). Отношение порядка обычно обозначается символом £. Элемент x частично упорядоченного множества (X,£) называется наибольшим (соответственно наименьшим), если для всякого y Î X верно y £ x (соответственно x £ y). Определение 2. Пусть (X,£) – частично упорядоченное множество. Нижней гранью множества его элементов
Нижняя грань обозначается через Заметим, что нижняя грань должна принадлежать множеству При n =2 нижняя грань множества Пример 1. Пусть (N+, |) – множество положительных натуральных чисел {1, 2, 3, …}, с отношением делимости: m | n Û n делится на m Û ($ k Î N+) mk = n. Тогда нижняя грань m Ù n равна наибольшему общему делителю, а m Ú n – наименьшему общему кратному. Определение 3. Частично упорядоченное множество (X,£) называется нижней (соответственно верхней) полурешеткой, если для любых Пример 2. Пусть X – множество. Частично упорядоченное множество (P(X),Í) подмножеств множества X с отношением включения будет решеткой.
Пример 3. Частично упорядоченное множество положительных натуральных чисел (N+, |) будет решеткой. Лемма 1. Если конечное частично упорядоченное множество (X,£) является нижней полурешеткой и имеет наибольший элемент, то оно будет решеткой. Доказательство. Пусть S= непусто и конечно. Поскольку X – нижняя полурешетка, то существует Определение 4. Пусть X – множество. Бинарное отношение R Í X´X называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно. Таким образом, R – отношение эквивалентности на X, если (1) (a,a)ÎR для всех a Î X, (2) aRb Þ bRa (3) для всех a, b, c Î X верна импликация aRb & bRc ÞaRc, Определение 5. Разбиением множества X называется множество { Xi: iÎI } попарно непересекающихся подмножеств Xi Í X таких, что Каждому отношению эквивалентности ~ на X соответствует разбиение { Xi: i Î I }, элементами которого являются подмножества, состоящие из эквивалентных элементов. Эти подмножества называются классами эквивалентности. Множество классов эквивалентности {Xi: iÎI} называется фактор-множеством множества X по отношению эквивалентности ~ и обозначается: X/~. Теорема 1. Пусть X – конечное множество. Множество отношений эквивалентности на X с отношением включения Í является решеткой. Доказательство. Множество отношений эквивалентности является нижней полурешеткой, ибо точной нижней гранью отношений эквивалентностей будет их пересечение. Оно будет иметь наибольший элемент X´X. Стало быть, оно будет решеткой, по лемме 1. Поскольку разбиения множества X взаимно однозначно соответствуют отношениям эквивалентности на X, то множество разбиений легко превратить в частично упорядоченное множество. Отношение порядка
В этом случае будет верно включение Следствие 1. Множество разбиений множества является решеткой. Упражнение 1. Пусть (X, R) – конечное частично упорядоченное множество. Будет ли решеткой множество отношений порядка rÍR, упорядоченное отношением Í?
|
||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 300; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.70.157 (0.005 с.) |
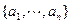 называется наибольший элемент подмножества
называется наибольший элемент подмножества .
. . Двойственно, как наименьший элемент множества
. Двойственно, как наименьший элемент множества 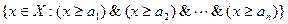 , определяется верхняя грань
, определяется верхняя грань  .
. , и, значит, удовлетворять неравенствам
, и, значит, удовлетворять неравенствам  для всех 1≤ i ≤ n. И среди элементов, удовлетворяющих этим неравенствам, она должна быть наибольшим элементом.
для всех 1≤ i ≤ n. И среди элементов, удовлетворяющих этим неравенствам, она должна быть наибольшим элементом. обозначается
обозначается  , а верхняя
, а верхняя 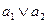 .
. множество
множество  . Положим
. Положим  . Для всех i=1, …, n имеет место z³ ai. И z – наименьший среди обладающих этим свойством. Стало быть, z =
. Для всех i=1, …, n имеет место z³ ai. И z – наименьший среди обладающих этим свойством. Стало быть, z = 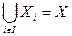 . С каждым разбиением { Xi: iÎI } можно связать отношение эквивалентности ~ на X, полагая x ~ y, если x и y являются элементами некоторого Xi.
. С каждым разбиением { Xi: iÎI } можно связать отношение эквивалентности ~ на X, полагая x ~ y, если x и y являются элементами некоторого Xi.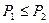 между разбиениями определяется как имеющее место тогда и только тогда, когда разбиение P1 мельче чем P2, т.е. когда верна импликация
между разбиениями определяется как имеющее место тогда и только тогда, когда разбиение P1 мельче чем P2, т.е. когда верна импликация .
.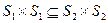 , и, стало быть, отношение эквивалентности, соответствующее разбиению P1, будет содержаться в отношении эквивалентности, соответствующем разбиению P2 . Мы установили биекцию между разбиениями и отношениями эквивалентности на множестве. Эта биекция сохраняет порядок. Получаем
, и, стало быть, отношение эквивалентности, соответствующее разбиению P1, будет содержаться в отношении эквивалентности, соответствующем разбиению P2 . Мы установили биекцию между разбиениями и отношениями эквивалентности на множестве. Эта биекция сохраняет порядок. Получаем


