Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Упражнение 1. Бросают две игральные кости. Найти вероятность выпадения 10 очков.Содержание книги
Поиск на нашем сайте
Решение. Напомним, что игральная кость – это кубик, каждой грани которого соответствует одно число от 1 до 6. В данном случае число всех исходов равно 62. Благоприятные исходы: (4,6), (5,5), (6,4). Отсюда вероятность равна p=3/36=1/12. Определение 3. Размещением называется произвольная инъекция f:{ x1, x2, ×××, xm } ®{ y1, y2, ×××, yn }. (В каждый ящик размещают не более одного предмета.) Теорема 1. Число размещений равно Доказательство. Первый предмет можно разместить n способами, второй – n-1, ×××, m- й – n-m+ 1. Получаем Упражение 2. В группе m студентов. Найти вероятность того, что найдется два студента, родившиеся в один день года. Решение. Полагаем, что год не високосный. Число всех вариантов 365m. Число неблагоприятных вариантов равно
Например, если число студентов равно 23, то вероятность равна примерно 0.5. Определение 4. Пусть заданы m ящиков. Упорядоченным размещениием предметов a1, a2, ×××, an называется указание последовательности предметов для каждого ящика, при котором каждый предмет участвует ровно один раз. Пример 1. На рисунке 2.1 показаны упорядоченные размещения предметов a, b по трем ящикам.
Рис. 2.1. Упорядоченные размещения Сначала размещается буква a в первый ящик и одним из четырех способов размещается b. Потом буква a размещается во второй ящик, в этом случае снова b размещается одним из четырех способов. Затем буква a размещается в третий ящик, буква b размещается одним из четырех способов. Всего получаем 12 упорядоченных размещений. Теорема 2. Число [m]n упорядоченных размещений n предметов в m ящиков равно m(m+1) ∙ ∙ ∙ (m+n-1). Доказательство. После размещения первого предмета в ящик одним из m способов
второй предмет может быть размещен одним из m+1 способов. Предположим, что уже размещено i-1 предметов, и пусть при k=1, 2, …, m в k -м ящике находится rk объектов. Тогда i -й объект может быть добавлен одним из (r1 +1) + (r2 +1) + ∙ ∙ ∙ + (rm +1) = i-1+m способов. Отсюда число всех упорядоченных размещений будет равно m(m+1) ∙ ∙ ∙ (n-1+ m). Сочетания Сочетанием элементов множества X называется подмножество конечного множества AÍX. Если |A|=k, |X|=n, то подмножество X называется с очетанием из n по k. Например, сочетания трех цветов семицветной радуги будут описываться подмножествами, состоящими из трех элементов выбранных из множества, состоящего из 7 элементов. Треугольник Паскаля и бином Ньютона. Для вычисления числа сочетаний построим таблицу, которая называется треугольником Паскаля. Она основана на следующей теореме: Теорема 1. Число сочетаний удовлетворяет соотношениям:
Доказательство. Число пустых подмножеств равно 1. Стало быть, Следующая таблица 2.1 строится на основе теоремы 1 и называется треугольником Паскаля. Таблица 2.1 Треугольник Паскаля
Теорема 2. Число сочетаний из n по k равно Доказательство. По индукции по n. При n=0 и k=0 получаем
Откуда формула верна для n +1 и всех k < n +1. Другой способ доказательства заключается в сопоставлении каждой инъекции ее образ. В этом случае, учитывая, что число инъекций с одинаковым образом равно k!, получаем Теорема 3. Доказательство. По индукции по n. Пусть формула верна для n. Тогда
Можно предложить также другое доказательство: Рассмотрим произведение n сомножителей (1 +x) (1 +x) × × × (1 +x). Сомножители будем рассматривать как ящики. Произведение равно сумме степеней xk, причем при каждом k слагаемые xk получаются выбором из ящиков k элементов, равных x. Отсюда коэффициент при xk будет равен количеству содержащих k элементов подмножеств множества, состоящего из n элементов.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 362; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.008 с.) |

 .
. .
. , где n =365. Получаем
, где n =365. Получаем 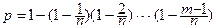 . Ниже приводится результаты вычислений значений вероятности при различных m:
. Ниже приводится результаты вычислений значений вероятности при различных m:
 ;
;  (при 0 < k < n).
(при 0 < k < n). . Подмножества, состоящие из n элементов, совпадают со всем множеством, отсюда
. Подмножества, состоящие из n элементов, совпадают со всем множеством, отсюда  . Число сочетаний, не содержащих n -й элемент, равно
. Число сочетаний, не содержащих n -й элемент, равно  , а содержащих –
, а содержащих –  . Следовательно, при 0 < k < n,
. Следовательно, при 0 < k < n,  .
. . Пусть теорема верна для n. С помощью теоремы 1 получаем
. Пусть теорема верна для n. С помощью теоремы 1 получаем .
. Þ
Þ  .
.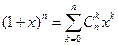 (Бином Ньютона).
(Бином Ньютона).