
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема 1. (Формула включения-исключения)Содержание книги
Поиск на нашем сайте
Доказательство. По индукции. При n =1, 2 утверждение очевидно. Заметим, что имеет место соотношение
Поскольку формула верна при n =2, то справедливо равенство
Отсюда мы видим, что
= В результате мы получили k -е слагаемое в формуле включения-исключения для множеств A1, …, An+1. Следовательно, эта формула верна для n+1 множеств. Что и требовалось доказать. Задача о встречах. В дождливую погоду n человек пришли в театр. Они сдают зонтики в гардероб. После окончания спектакля получают зонтики обратно, в случайном порядке. Какова вероятность того, что каждый из них получит чужой зонтик? Задача сводится к нахождению числа перестановок элементов множества {1, 2, ∙ ∙ ∙, n}, не имеющих неподвижных точек. Пусть Si состоит из перестановок, оставляющих неподвижной точку i. Вычислим | S1È S2 È ∙ ∙ ∙È Sn |. Искомая вероятность будет равна
Получаем Задача о счастливых билетах. Требуется найти число решений уравнения x1+x2+x3 = y1+y2+y3, где 0 £ xi, yi £ 9. Решение. Подстановка x4=9-y1 , x5=9-y2 , x6=9-y3 устанавливает биекцию между решениями этого уравнения и уравнения x1+x2+x3 + x4+x5+x6 = 27, где 0£ xi £9. Найдем число разложений x1+x2+x3 + x4+x5+x6 = 27, где 0£ xi £9. Пусть U1 – число разложений с x1³10, U2 – число разложений с x2³10, ∙∙∙ U6 – число разложений с x6³10. Тогда | Ui ÇUjÇUk | = 0при | { i,j,k } |= 3. Вычислим число разложений, не удовлетворяющих неравенствам 0£ xi £9. Оно равно | U1 ÈU2ÈU3 ÈU4 ÈU5 ÈU6 | = 6 |U1|─ 15 |U1ÇU2|, где | U1| ─ число решений уравнения (x1─10)+x2+x3 + x4+x5+x6 = 27─10, а |U1ÇU2| ─ число решений уравнения (x1─10)+(x2─10)+x3 + x4+x5+x6 = 27─10-10. Получаем | U1 ÈU2ÈU3 ÈU4 ÈU5 ÈU6 | = Из числа всех разложений вычитаем разложения с xi ≥10. Получаем окончательный ответ
Функция Эйлера. Пусть n – положительное натуральное число, j (n) – количество натуральных чисел 0< d £ n, взаимно простых c n (т.е. не имеющих одинаковых делителей, кроме 1). Например, при n =10, d Î{1, 3, 7, 9} и j (10) = 4. Функция j (n) называется функцией Эйлера. Теорема 2.
где q 1, …, qт являются различными простыми делителями числа n. Доказательство. Находим число не взаимно простых с n по формуле включения и исключения, пользуясь тем, что количество делящихся среди {1,2, …, n } на число q равно n/q. Затем это число отнимаем от n. Разбиения Напомним, что разбиением множества A называется семейство { Ai } его непустых попарно непересекающихся подмножеств, таких что È iAi = A. Подмножества Ai называются блоками разбиения. Если в семействе учитывается порядок подмножеств, и если допускаются пустые блоки, то оно называется упорядоченным разбиением. Упорядоченные разбиения и обобщенный бином Ньютона. Будем говорить, что упорядоченное разбиение (A 1 , A 2 , ×××, Am) множества E= { e 1, e 2, ×××, en } имеет тип (k1, k2, ×××, km), если |A1| = k1, |A2| = k2,×××, |Am| = km. Число таких разбиений обозначается через P(k1, k2, ×××, km) или Pn(k1, k2, ×××, km), где n= k1 + k2 + ××× + km. Лемма 1. Доказательство. Подмножество A1 можно выбрать
Поскольку n – k1 – ∙∙∙ – km-1 = km, то после сокращения дроби получаем нужное равенство. Теорема 1.
Доказательство. Рассмотрим как ящики сомножители произведения
Произведение состоит из слагаемых вида Разбиения и перечисление сюръекций. Пусть {B1, ×××, Bk } – разбиение множества X, состоящего из n элементов. Обозначим через P k(X) множество разбиений X на k блоков, а через P(X) – множество всех разбиений. Число S(n,k) = | P k(X)| называется числом Стирлинга второго рода, Bn=| P (X)| – числом Белла. Ясно, что Пример 2. Число S(4,2) равно 7, ибо все разбиения множества {1,2,3,4, 5, 6, 7} на два блока исчерпываются следующими: {{1},{2,3,4}}, {{2},{1,3,4}}, {{3},{1,2,4}}, {{4},{1,2,3}}, {{1,2},{3,4}}, {{1,3},{2,4}}, {{1,4},{2,3}}. Теорема 2. Имеют место следующие свойства чисел Стирлинга второго рода: · S(n,k)=0, при k > n. · S(n,0)=0 и S(n,n)=1, при n>0. · S(n,k)=S(n-1,k-1)+kS(n-1,k), при 0 < k < n. Доказательство. Докажем последнее соотношение. Множество разбиений множества {1,2, ×××,n} состоит из двух классов: (1) разбиения, содержащие блок {n}; (2) разбиения, для которых n принадлежит блокам, имеющим более одного элемента. В первом классе S(n-1,k-1) разбиений. Во втором классе получаем kS(n-1,k) разбиений, ибо каждому разбиению множества {1, 2, ×××, n-1} на k блоков B1, B2, ×××, Bk соответствует k разбиений B1 È {n}, B2, ×××, Bk, B1, B2È {n}, ×××, Bk, ××××××××××××××××××××××××××××××× B1, B2 , ×××, Bk È {n}, Следовательно, S(n,k)=S(n-1,k-1)+kS(n-1,k), при 0 < k < n. Составим таблицу 2.3 для нахождения чисел Стирлинга Таблица 2.3 Числа Стирлинга
Пример 3. Найдем число сюръекций {1,2,3,4,5,6}®{1,2,3,4}. Оно равно 4!S(6,4). Число S(6,4) находим из таблицы. Отсюда искомое число = 4!∙65 = 1∙2∙3∙4∙65 = 1560. Положим B0=1. Число Белла Bn можно вычислить по формуле Теорема 3. Доказательство. Множество разбиений X= {1,2, ×××, n+ 1} состоит из классов, зависящих от блока A содержащего n+ 1. Для таких A будет справедливо включение X\A Í{1, 2, ×××, n }. Отсюда каждое разбиение можно получить, выбрав блок A ' n +1 и разбиение pÎP(X\A). Выбор блока A с | A|=k +1,будет осуществляться выбором подмножества из {1,2, ×××, n }, состоящего из k элементов. Следовательно, Упражнения Размещения 1. Сколькими способами можно составить трехцветный флаг (рис. 2.4) из материа-
Рис. 2.4. Пример флага лов семи цветов. Одна из полос должна быть красной. Ответ: 73 - 63. 2. Скольким способами можно раскрасить 4 полосы флага в 7 цветов, так, чтобы по крайней мере две полосы имели одинаковый цвет? Ответ: 3. Скольким способами можно раскрасить 4 полосы флага в 7 цветов, так, чтобы рядом находящиеся полосы имели различные цвета? Ответ: 7∙ 63. 4. Сколько перестановок p: {1,2, ∙∙∙, 5} ® {1,2, ∙∙∙, 5} удовлетворяют условию p (1)¹2? 5. В соревновании принимают участие 8 спортсменов. Сколькими способами могут быть разделены медали (золотые, серебряные и бронзовые?) 6. Найти число функций {1,2,3}®{1,2,3,4,5}. 7. Найти число инъекций {1,2,3}®{1,2,3,4,5}. 8. Сколько чисел между 1000 и 10000 состоят из различных цифр? 9. Сколько семизначных чисел (не начинающихся с 0) состоят из различных цифр? Сочетания 10. Доказать тождества непосредственно из определения числа (1) (2) (3) 11. Из содержащей 52 карты колоды вынимают 10 карт. Какова вероятность, что среди них окажется (1) хотя бы один туз? Ответ: (2) ровно один туз? Ответ: (3) не менее двух тузов? Ответ: (4) ровно два туза? Ответ: 12. Из содержащей 52 карты колоды вынимают 10 карт. Какова вероятность, что среди них окажется (1) 4 туза, 2 короля, 3 дамы; (2) 2 туза, 2 короля, 2 дамы; (3) 1 туз, 1 королm, 2 дамы, 3 десятки; (4) 4 туза, 4 короля, 2 дамы; (5) 2 туза, 3 короля, 1 дама, 1 десятка; (6) 3 туза, 2 короля, 4 дамы; 13. Разложением числа m называется конечная последовательность (x1, x2, ×××, xn) неотрицательных целых чисел, таких что x1+ x2+ ××× + xn = m. Сколько разложений числа 19 состоит лишь из чисел 2 и 3? Указание. Если в разложении p двоек и q троек, то 2p + 3q = 19. Отсюда получаем следующие варианты разложения, приведенные в таблице 2.4. Таблица 2.4 Варианты разложения
Ответ: 14. Сколько разложений числа 12 состоит из чисел 2 и 3? Ответ: 15. Сколькими способами можно разложить число 1024 в произведение трех натуральных чисел, каждое из которых больше 1? Указание. Это число решений уравнения x1+ x2,+ x3 = 10, где xi >0. Ответ: 16. Сколько существует на плоскости непрерывных путей из точки (0,0) в точку (n,n)Î N ´ N, состоящих из направленных отрезков, вектора которых равны (1,0) или (0,1)? 17. Найти число непрерывных путей в декартовой плоскости, соединяющих точку (0,0) с точкой (m,n)Î N ´ N, проходящих через точку (p,q) и состоящих из направленных отрезков, вектора которых равны (1,0) или (0,1)? 18. Найти число решений уравнения x1+ x2+ x3+ x4 + x5 = 20, где xi > 0. 19. Найти число решений уравнения x1+ x2+ x3+ x4 + x5 = 15, где xi ³ 0. 20. Найти число возрастающих функций {1,2,3,4,5}®{1,2,3,4,5,6,7}. 21. Найти число неубывающих сюръекций {1,2,3,4,5,6,7}®{1,2,3,4,5}. 22. Найти число неубывающих функций {1,2,3,4,5}®{1,2,3,4,5}. 23. Найти количество десятичных неотрицательных целых чисел, состоящих из не более чем n цифр, расположенных в неубывающем порядке (цифра 0 не допускается первой для ненулевых чисел). Например, при n =2, такие числа будут равны 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, 15, 16, 17, 18, 19, 22, 23, ∙ ∙ ∙, 89, 99. Ответ: 24. Найти количество десятичных неотрицательных целых чисел, состоящих цифр, расположенных в возрастающем порядке. Ответ: 25. Найти число неотрицательных целых чисел, десятичная запись которых состоит из n разрядов и содержит все цифры, расположенные в невозрастающем порядке. Ответ: 26. Какое количество m´n –матриц можно составить из неотрицательных целых чисел aij ³ 0, таких что S aij = k. Ответ: Упорядоченные разбиения 27. Десять человек разбились на 5 групп по 2 человека в каждой. Скольким способами это можно сделать? Указание. Упорядоченных разбиений 10!/(2!2!2!2!2!), при перестановках групп получаются одинаковые разбиения, отсюда искомое число = 10!/(2!2!2!2!2!)/5! = 1×3×5×7×9 = 945. 28. В группе 20 студентов. Одному человеку положено выдать надбавку к стипендии в размере 1000 рублей. Двум – по 500, трем по 300. Сколькими способами это можно сделать? 29. Сколько существует шашечных позиций, состоящих из 10 белых и 10 черных шашек? 30. Сколько различных слов можно составить с помощью перестановок всех букв слова МАТЕМАТИКА. Словом называется произвольная конечная последовательность букв. 31. Оценить сверху число шахматных позиций, содержащих все фигуры и пешки? 32. В урне находится k шаров. Каждый шар может иметь либо белый, либо черный, либо красный цвет. Какова вероятность того, что один шар белый, один – черный? (а остальные красные.) Ответ: k(k-1)/3k. 33. Найти коэффициент при 34. Найти (x1 + x2 + x3)4. 35. Сколько путей, составленных из направленных отрезков единичной длины существует в трехмерной решетке из (0,0,0) в (p,q,r). Вектора отрезков равны (1,0,0), (0,1,0), (0,0,1).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 321; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.011 с.) |


 . Предположим, что для n множеств утверждение верно. Докажем ее для n+1. Имеем по формуле включения-исключения для n множеств A1 Ç An+1, A2 Ç An+1, …, An Ç An+1 :
. Предположим, что для n множеств утверждение верно. Докажем ее для n+1. Имеем по формуле включения-исключения для n множеств A1 Ç An+1, A2 Ç An+1, …, An Ç An+1 :
 .
. содержит слагаемое, равное сумме
содержит слагаемое, равное сумме  и соответствующее первому слагаемому в формуле включения-исключения для n +1 множеств. Объединим k -е слагаемое определенное в формуле для
и соответствующее первому слагаемому в формуле включения-исключения для n +1 множеств. Объединим k -е слагаемое определенное в формуле для  и (k-1)-е слагаемое в формуле включения-исключения для
и (k-1)-е слагаемое в формуле включения-исключения для  . В силу
. В силу  =
=  , будем иметь
, будем иметь -
-  =
= .
.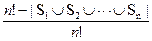 .
.
 . Отсюда число перестановок, не имеющих неподвижных точек, равно
. Отсюда число перестановок, не имеющих неподвижных точек, равно 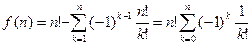 . Искомая вероятность равна
. Искомая вероятность равна  . Число f (n) будет ближайшим к дроби
. Число f (n) будет ближайшим к дроби  целым числом. При n ®¥ вероятность стремится к
целым числом. При n ®¥ вероятность стремится к 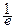 .
.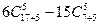 .
. .
.
 .
. способами. Подмножество A2 выбирается из оставшихся n-k1 элементов, его можно будет выбрать
способами. Подмножество A2 выбирается из оставшихся n-k1 элементов, его можно будет выбрать  способами. Подмножество A3 –
способами. Подмножество A3 – 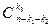 способами, и т.д. Выбор подмножества Am определен предшествующими подмножествами. Отсюда получаем
способами, и т.д. Выбор подмножества Am определен предшествующими подмножествами. Отсюда получаем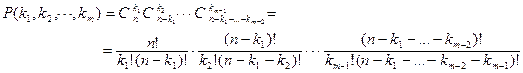 .
. .
. .
. . Каждое такое слагаемое встречается столько раз, сколько существует упорядоченных разбиений множества ящиков. Разбиение будет состоять из следующих подмножеств: первое подмножество состоит из ящиков, откуда выбран x1, второе состоит из подмножеств, откуда выбран x2 и т.д. Отсюда коэффициент при
. Каждое такое слагаемое встречается столько раз, сколько существует упорядоченных разбиений множества ящиков. Разбиение будет состоять из следующих подмножеств: первое подмножество состоит из ящиков, откуда выбран x1, второе состоит из подмножеств, откуда выбран x2 и т.д. Отсюда коэффициент при  . Каждому разбиению мы сопоставили отношение эквивалентности и заметили, что разбиения составляют решетку относительно включения соответствующих отношений эквивалентности. Отсюда множество разбиений будет решеткой относительно неравенства p£s Û каждый блок BÎs является объединением некоторых блоков из p. Например, {{1},{2},{3}}£{{1},{2,3}}.Пусть sn,k – число сюръекций f:{1,2, ×××,n}® {1,2, ×××, k}. Каждой сюръекции соответствует разбиение {f –1(y): 1 £ y £ k}. Отсюда легко видеть, что sn,k =k!S(n,k). Положим S(0,0)=1.
. Каждому разбиению мы сопоставили отношение эквивалентности и заметили, что разбиения составляют решетку относительно включения соответствующих отношений эквивалентности. Отсюда множество разбиений будет решеткой относительно неравенства p£s Û каждый блок BÎs является объединением некоторых блоков из p. Например, {{1},{2},{3}}£{{1},{2,3}}.Пусть sn,k – число сюръекций f:{1,2, ×××,n}® {1,2, ×××, k}. Каждой сюръекции соответствует разбиение {f –1(y): 1 £ y £ k}. Отсюда легко видеть, что sn,k =k!S(n,k). Положим S(0,0)=1. . Рассмотрим более простые формулы для нахождения чисел Белла.
. Рассмотрим более простые формулы для нахождения чисел Белла. , " n ³ 0.
, " n ³ 0. .
. .
.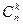
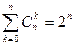 ,
,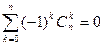 ,
, .
.






 .
. = 12.
= 12. = 36.
= 36. = 36.
= 36.
 .
. .
.
 в разложении степени
в разложении степени  в сумму однородных одночленов.
в сумму однородных одночленов.


