
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция № 2. Ременные передачи.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Вопросы, изложенные в лекции: 1. Общие сведения о передачах. 2. Ременные передачи.
Передачей будем называть устройство, предназначенное для передачи энергии из одной точки пространства в другую, расположенную на некотором расстоянии от первой. В зависимости от вида передаваемой энергии передачи делятся на механические, электрические, гидравлические, пневматические и т.п. В курсе деталей машин изучаются, в основном, механические передачи. Механической передачей называют устройство (механизм, агрегат), предназначенное для передачи энергии механического движения, как правило, с преобразованием его кинематических и силовых параметров, а иногда и самого вида движения. Наибольшее распространение в технике получили передачи вращательного движения, которым в курсе деталей машин уделено основное внимание (далее под термином передача подразумевается, если это не оговорено особо, именно передача вращательного движения). Классификация механических передач вращательного движения: 1. По способу передачи движения от входного вала к выходному: 1.1. Передачи зацеплением: 1.1.1. с непосредственным контактом тел вращения - зубчатые, червячные, винтовые; 1.1.2. с гибкой связью - цепные, зубчато-ременные. 1.2. Фрикционные передачи: 1.2.1. с непосредственным контактом тел вращения – фрикционные; 1.2.2. с гибкой связью - ременные. 2. По взаимному расположению валов в пространстве: 2.1. с параллельными осями валов - зубчатые с цилиндрическими колесами, фрикционные с цилиндрическими роликами, цепные; 2.2. с пересекающимися осями валов - зубчатые и фрикционные конические, фрикционные лобовые; 2.3. с перекрещивающимися осями - зубчатые - винтовые и коноидные, червячные, лобовые фрикционные со смещением ролика. 3. По характеру изменения угловой скорости выходного вала по отношению к входному: редуцирующие (понижающие) и мультиплицирующие (повышающие). 4. По характеру изменения передаточного отношения (числа): передачи с постоянным (неизменным) передаточным отношением и передачи с переменным (изменяемым или по величине, или по направлению или и то и другое вместе) передаточным отношением. 5. По подвижности осей и валов: передачи с неподвижными осями валов - рядовые (коробки скоростей, редукторы), передачи с подвижными осями валов (планетарные передачи, вариаторы с поворотными роликами). 6. По количеству ступеней преобразования движения: одно-, двух-, трех-, и многоступенчатые. 7. По конструктивному оформлению: закрытые и открытые (безкорпусные). Главными характеристиками передачи, необходимыми для ее расчета и проектирования, являются мощности и скорости вращения на входном и выходном валах - Pвх, Pвых, wвх, wвых. В технических расчетах вместо угловых скоростей обычно используются частоты вращения валов - nвх и nвых. Соотношение между частотой вращения n (общепринятая размерность 1/мин) и угловой скоростью w (размерность в системе SI 1/с) выражается следующим образом:
Отношение мощности на выходном валу передачи Pвых (полезной мощности) к мощности Pвх, подведенной к входному валу (затраченной), принято называть коэффициентом полезного действия (КПД):
Отношение потерянной в механизме (машине) мощности (Pвх - Pвых) к ее входной мощности называют коэффициентом потерь, который можно выразить следующим образом:
Следовательно сумма коэффициентов полезного действия и потерь всегда равна единице:
Для многоступенчатой передачи, включающей k последовательно соединенных ступеней, общий КПД равен произведению КПД отдельных ступеней:
Следовательно КПД машины, содержащей ряд последовательных передач, всегда будет меньше КПД любой из этих передач. Силовые показатели передачи определяются по известным из теории механизмов и машин (ТММ) формулам: усилие, действующее по линии движения на поступательно движущейся детали (например, на ползуне кривошипно-ползунного механизма) F=P/v, где P - мощность, подведенная к этой детали, а v - ее скорость; аналогично, момент, действующий на каком-либо из валов передачи (редуктора, коробки передач, трансмиссии), T=P/w, где P - мощность, подведенная к этому валу, а w - скорость его вращения. Используя соотношение (2.1), получаем формулу, связывающую момент, мощность и частоту вращения:
Окружная (касательная) скорость в любой точке вращающегося элемента (колеса, шкива, вала), лежащей на диаметре D этого элемента будет равна:
При этом тангенциальную (окружную или касательную) силу можно вычислить по следующей формуле:
Передаточное отношение - это отношение скорости входного звена к скорости выходного звена, что для вращательного движения выразится следующим образом:
где верхний знак (плюс) соответствует одинаковому направлению вращения входного и выходного звеньев (валов), а нижний - встречному. Однако в технических расчетах (особенно прочностных) направление вращения чаще всего не имеет решающего значения, поскольку оно не определяет нагрузки, действующие в передаче. В таких расчетах используется передаточное число, которое представляет собой абсолютную величину передаточного отношения:
В многоступенчатой передаче с последовательным расположением k ступеней (что чаще всего наблюдается в технике) передаточное число и передаточное отношение определяются следующими выражениями:
Среди множества разнообразных передач вращательного движения достаточно простыми конструктивно (по устройству) являются передачи с гибкой связью, принцип работы которых строится на использовании сил трения или зубчатого зацепления - это ременные передачи.
Ременная передача – это механизм, предназначенный для передачи вращательного движения посредством фрикционного взаимодействия или зубчатого зацепления замкнутой гибкой связи – ремня с жесткими звеньями – шкивами, закрепленными на входном и выходном валах механизма. Ременная передача (рис. 2.1) состоит из двух или большего числа шкивов, насаженных на валы, участвующие в передаче вращательного движения, и гибкой связи, называемой ремнем, которая охватывает шкивы с целью передачи движения от ведущего шкива ведомому (или ведомым) и взаимодействует с ними посредством сил трения или зубчатого зацепления. Основную часть лекции посвятим фрикционным ременным передачам, поэтому далее под термином ременная передача, если это не будет оговорено особо, будем понимать именно фрикционную передачу.
Ременные передачи трением – наиболее старый и простой по конструкции вид передачи. Эти передачи и в настоящее время находят достаточно широкое применение, они широко применяются на быстроходных ступенях привода (передача вращения от электродвигателей к последующим механизмам). В двигателях внутреннего сгорания МГКМ ременные передачи применяются для привода вспомогательных агрегатов (вентилятор, насос системы водяного охлаждения, электрический генератор), а зубчатоременная передача применяется в некоторых автомобильных двигателях для привода газораспределительного механизма. Достоинства ременных передач: 1. Простота конструкции и низкая стоимость. 2. Возможность передачи движения на достаточно большие расстояния (до 15 м). 3. Возможность работы с большими скоростями вращения шкивов. 4. Плавность и малошумность работы. 5. Смягчение крутильных вибраций и толчков за счет упругой податливости ремня. 6. Предохранение механизмов от перегрузки за счет буксования ремня при чрезмерных нагрузках. Недостатки ременных передач: 1. Относительно большие габариты. 2. Малая долговечность ремней. 3. Большие поперечные нагрузки, передаваемые на валы и их подшипники. 4. Непостоянство передаточного числа за счет проскальзывания ремня. 5. Высокая чувствительность передачи к попаданию жидкостей (воды, топлива, масла) на поверхности трения. Классификация ременных передач: 1. По форме поперечного сечения ремня: плоскоременные (поперечное сечение ремня имеет форму плоского вытянутого прямоугольника, рис. 2.1.а); клиноременные (поперечное сечение ремня в форме трапеции рис. 2.1.б); поликлиноременные (ремень снаружи имеет плоскую поверхность, а внутренняя, взаимодействующая со шкивами, поверхность ремня снабжена продольными гребнями, выполненными в поперечном сечении в форме трапеции рис. 2.1.г); круглоременные (поперечное сечение ремня имеет форму круга рис. 2.1.в); зубчатоременная (внутренняя, контактирующая со шкивами, поверхность плоского ремня снабжена поперечными выступами, входящими в процессе работы передачи в соответствующие впадины шкивов). 2. По взаимному расположению валов и ремня: с параллельными геометрическими осями валов и ремнем, охватывающим шкивы в одном направлении – открытая передача (шкивы вращаются в одном направлении); с параллельными валами и ремнем, охватывающим шкивы в противоположных направлениях – перекрестная передача (шкивы вращаются во встречных направлениях); оси валов перекрещиваются под некоторым углом (чаще всего 90°) – полуперекрестная передача. 3. По числу и виду шкивов, применяемых в передаче: с одношкивными валами; с двушкивным валом, один из шкивов которого холостой; с валами, несущими ступенчатые шкивы для изменения передаточного числа (для ступенчатой регулировки скорости ведомого вала). 4. По количеству валов, охватываемых одним ремнем: двухвальная, трех -, четырех - и многовальная передача. 5. По наличию вспомогательных роликов: без вспомогательных роликов, с натяжными роликами; с направляющими роликами.
Геометрические соотношения в ременной передаче рассмотрим на примере открытой плоскоременной передачи (рис. 2.2). Межосевое расстояние а – это расстояние между геометрическими осями валов, на которых установлены шкивы с диаметрами D1 (он, как правило, является ведущим) и D2 (ведомый шкив). При расчетах клиноременных передач для ведущего и ведомого шкивов используются расчетные диаметры dр1 и dр2. Угол между ветвями охватывающего шкивы ремня - 2g, а угол охвата ремнем малого (ведущего) шкива (угол, на котором ремень касается поверхности шкива) a1. Как видно из чертежа (рис. 2.2) половинный угол между ветвями составит
а так как этот угол обычно невелик, то во многих расчетах допустимым является приближение g» sing, то есть
Используя это допущение угол охвата ремнем малого шкива можно представить в следующем виде
в радианной мере, или
в градусах. Длину ремня при известных названных выше параметрах передачи можно подсчитать по формуле
Однако, весьма часто ремни изготавливаются в виде замкнутого кольца известной (стандартной) длины. В этом случае возникает необходимость уточнять межосевое расстояние по заданной длине ремня
С целью обеспечения стабильности работы передачи обычно принимают для плоского ремня а для клинового – где hp – высота поперечного сечения ремня (толщина ремня). В процессе работы передачи ремень обегает ведущий и ведомый шкивы, чем короче ремень (чем меньше Lp) и чем быстрее он движется (чем больше его скорость Vp), тем чаще происходит контактирование его рабочей поверхности с поверхностью шкивов и тем интенсивнее он изнашивается. Поэтому отношение Vp / Lp (его размерность в системе СИ – с-1) характеризует долговечность ремня в заданных условиях его работы – чем больше величина этого отношения, тем ниже при прочих равных условиях долговечность ремня. Обычно принимают для плоских ремней Vp / Lp = (3…5) с-1, для клиновых - Vp / Lp = (20…30) с-1. Силовые соотношения в ременной передаче. Необходимым условием нормальной работы любой фрикционной передачи, включая ременные, является наличие сил нормального давления между поверхностями трения. В ременной передаче такие силы возможно создать только за счет предварительного натяжения ремня. При неработающей передаче силы натяжения обеих ветвей будут одинаковыми (обозначим их F0, как на рис 2.3.а). В процессе работы передачи набегающая на этот шкив ветвь ремня за счет трения ведущего шкива о ремень получает дополнительное натяжение (обозначим силу натяжения этой ветви F1), в то время как вторая, сбегающая с ведущего шкива, ветвь ремня несколько ослабляется (её силу натяжения обозначим F2, см. рис. 2.3.б). Тогда, очевидно, окружное усилие, передающее рабочую нагрузку С учетом высказанных соображений и используя известные соотношения нетрудно получить зависимость для вычисления оптимальной величины сил предварительного натяжения ремня
а из последнего, выражая тяговое усилие на ведущем шкиве в соответствии с (2.8), получим
где индексы «1» указывают на параметры, относящиеся к ведущему шкиву передачи. Если величину предварительного натяжения ремня сделать меньшей по сравнению с представленным в выражении (2.19), то произойдет буксование (проскальзывание) ремня, и переданная на выходной вал мощность уменьшится до величины, соответствующей фактическому значению силы предварительного натяжения. Если же силы предварительного натяжения ветвей будут больше оптимальной величины, необходимой для передачи заданной мощности, то возрастёт относительная доля мощности, затраченная на упругое скольжение ремня по шкивам, что также приведет к снижению мощности на выходном валу передачи, то есть к уменьшению её КПД. Аналогично, сила натяжения ведущей ветви составит
Отношение разности сил натяжения в ветвях ремня работающей передачи к сумме этих сил называется коэффициентом тяги (j).
Коэффициент тяги характеризует качество работы передачи. Его оптимальное значение нетрудно найти, используя выражение (2.18),
Как видно из последнего выражения оптимальная величина коэффициента тяги не зависит ни от передаваемой мощности, ни от предварительного натяжения ремня, а только лишь от свойств фрикционной пары материалов, из которых изготовлены ремень и шкив, и от конструктивных параметров передачи. Численные значения j0 для ремней из различных материалов и угла охвата ремнем стального ведущего шкива, равного 180°, представлены в табл. 2.1.
Кинематика ременной передачи. Как показано выше сила натяжения ведущей ветви ремня существенно превышает силу натяжения свободной ветви (F1>F2). Отсюда следует, что удлинение каждого отдельно взятого элемента ремня меняется в зависимости от того, на какую его ветвь этот элемент в данный момент времени попадает. Изменение этой элементарной части ремня может происходить только в процессе ее движения по шкивам. При этом, проходя по ведущему шкиву (при переходе с ведущей ветви на свободную), эта элементарная часть укорачивается, а при движении по ведомому шкиву (переходя со свободной ветви ремня на его ведущую ветвь) – удлиняется. Изменение длины части ремня, соприкасающейся с поверхностью шкива, возможно только с её частичным проскальзыванием. Изложенные соображения позволяют сформулировать два важнейших следствия неодинаковой загрузки ведущей и холостой ветвей ремня: Работа ременной передачи без скольжения ремня по рабочей поверхности шкивов невозможна. Скорости движения ведущей и свободной ветвей ремня различны, а следовательно различны и скорости рабочих поверхностей ведущего и ведомого шкивов. Окружная скорость рабочей поверхности ведущего шкива всегда больше окружной скорости ведомого шкива (V1 > V2). Отношение разности между окружными скоростями на рабочей поверхности ведущего и ведомого шкивов к скорости ведущего шкиве называют коэффициентом скольжения передачи (x).
где индекс «1» соответствует ведущему, а индекс «2» - ведомому шкивам. Выражая в (2.23) линейные (тангенциальные) скорости рабочих поверхностей шкивов через угловую скорость и их радиус, нетрудно получить выражение, определяющее передаточное число ременной передачи через ее конструктивные параметры:
Рекомендуемые значения передаточных чисел фрикционных ременных передач представлены в табл. 2.2. Тяговая способность и долговечность ремня являются основными критериями работоспособности ременной передачи. Проектный расчет ременной передачи обычно выполняется по тяговой способности, а расчет долговечности при этом является проверочным. Проиллюстрируем поведение ременной передачи графиком, на котором по оси абсцисс отложен коэффициент тяги, а по оси ординат - коэффициент скольжения и КПД (рис. 2.4). На графике можно выделить три основных зоны:
1 зона, где 0 £ j £ j0, эту область называют зоной упругого скольжения; 2 зона, где j0 £ j £ jmax, её называют зоной частичного буксования; 3 зона, где j > jmax, эту область называют зоной полного буксования. В зоне упругого скольжения коэффициент скольжения растет линейно с увеличением коэффициента тяги, одновременно возрастает и КПД передачи, достигая максимального значения при оптимальной величине коэффициента тяги j0. Дальнейшее увеличение коэффициента тяги приводит к частичному буксованию ремня, коэффициент скольжения растет нелинейно и намного интенсивнее по сравнению с 1 зоной, а КПД также нелинейно и интенсивно снижается. При достижении коэффициентом тяги величины jmax наступает полное буксование передачи (ведомый шкив останавливается), величина скольжения становится равной единице, а КПД падает до нулевого значения. Представленный выше анализ показывает, что наиболее благоприятной для работы передачи является область коэффициентов тяги, прилегающая к его оптимальному значению, поскольку именно в этой области передача обладает максимальным КПД. При этом величина упругого скольжения для разных типов ремней лежит в пределах 1…2%, а КПД для передачи плоским ремнем можно принять равным 0,95…0,97, клиновым или поликлиновым – 0,92…0,96. Напряжения в ремне. Напряжения, возникающие в ведущей ветви ремня от действия рабочих нагрузок, нетрудно определить, разделив (2.20) на площадь поперечного сечения ремня Aр,
Кроме рабочих напряжений, обусловленных предварительным натяжением ремня и тяговым усилием, участвующем в передаче мощности от ведущего шкива к ведомому, в ремне возникают еще два вида дополнительных напряжений – изгибные и центробежные. Изгибные напряжения возникают при изгибе ремня в момент огибания им шкивов, при этом наибольшая величина изгибных напряжений соответствует меньшему радиусу изгиба, то есть максимальные напряжения изгиба возникают в ремне при обегании меньшего (чаще всего являющегося ведущим) шкива. Учитывая последнее, на основе формул сопротивления материалов получаем
где E – модуль упругости материала ремня (см. табл. 2.3), y0 – расстояние от нейтрального слоя до наружного (растянутого) волокна ремня, D1 – диаметр наименьшего шкива передачи. Принимая для плоского ремня y0 = d / 2, где d - толщина ремня, а для клинового - y0 = (0,25…0,38)h, где h – толщина ремня, получаем: для плоского ремня
а для клинового ремня
Таким образом, напряжения изгиба пропорциональны толщине ремня и обратнопропорциональны диаметру наименьшего из шкивов, работающих в передаче. Часть ремня, прилегающая к шкиву участвует в круговом движении, что обусловливает действие на неё центробежных сил, вызывающих в ремне растягивающие напряжения. Напряжения от центробежных сил можно вычислить по простому соотношению
где r - средняя плотность материала ремня, а Vр – средняя скорость движения ремня, обегающего шкив. выражая скорость ремня через частоту вращения и диаметр наименьшего шкива, получим
Как видим, напряжения, вызванные в ремне действием центробежных сил, квадратично зависят как от частоты вращения наименьшего шкива, так и от его диаметра. На внешней стороне ремня все три вида названных напряжений являются растягивающими и потому суммируются. Таким образом, максимальные растягивающие напряжения в ремне
Анализ реальных передач показывает, что напряжения от изгиба sи и от действия центробежных сил sц обычно сравнимы и часто даже превосходят по величине напряжения от рабочей нагрузки sр. При этом следует учитывать, что увеличение sи не способствует повышению тяговой способности передачи, с другой стороны, эти напряжения, периодически меняясь, являются главной причиной усталостного износа ремней. Расчет ременных передач основан на общей теории ременных передач и экспериментальных данных. При этом формула Эйлера и зависимость (2.31) непосредственно не используются, а влияние дополнительных напряжений sи и sц на долговечность передачи учитывают при выборе её геометрических параметров (a, D1, a и др.) и допускаемых напряжений [st]0 и [st], используемых в расчете. При проектном расчете диаметр малого шкива D1 можно оценить по модифицированной формуле М.А. Саверина
где вращающий момент T1 в Нм, диаметр малого шкива D1 в мм, а эмпирический коэффициент KD для различных типов передач представлен в табл. 2.4. Полученный расчетом диаметр малого шкива увеличивается до ближайшего большего стандартного линейного размера. Далее расчет плоскоременной передачи базируется на показателях тяговой способности и сводится к выполнению основного условия прочности ремня
где Ft – окружная сила, передаваемая ремнем, Н; sFt – расчетное полезное напряжение, МПа; b и d - ширина и толщина ремня, мм. При этом допускаемое полезное напряжение определяется исходя из опытных данных, полученных при стандартном испытании ремня, с введением поправок на пространственное расположение передачи, угол обхвата на малом шкиве и скорость движения ремня (уменьшение сцепления центробежными силами), на режим работы передачи. Обычно такой расчет предполагает минимальный срок службы передачи (ремня) 2000 ч. Однако, экспериментально установлено, что для ремней не удается установить предел неограниченной выносливости, а ресурс ремня, выраженный числом пробегов за срок службы N, связан с наибольшим напряжением, вычисленным по зависимости (2.31), соотношением
Вводя в рассмотрение число пробегов ремня в секунду
где zш – число шкивов, огибаемых ремнем. Формулы (2.34) и (2.35) получены при диаметре малого шкива D1 = 200 мм, u» 1 (угол охвата малого шкива a = 180°) и s0 = 1,2 МПа. Опытные значения коэффициентов C и m для некоторых типов ремней представлены в табл. 2.5.
Особенности конструкции, работы и расчета клиноременных и поликлиноременных передач. Клиновые ремни имеют трапециевидное поперечное сечение, а поликлиновые – выполненную в форме сочленённых основаниями клиньев рабочую часть (рис. 2.5). Угол клина для обоих видов ремней одинаков и составляет 40°. На шкивах такой передачи выполняются соответствующие сечению рабочей части ремня канавки, называемые ручьями. Профили ремней и ручьёв шкивов контактируют только боковыми (рабочими) поверхностями (рис. 2.6). В клиноременных передачах для снижения изгибных напряжений часто применяют комплект из нескольких ремней (2…6), работающих параллельно на одной паре шкивов. размеры сечений клиновых ремней стандартизованы (ГОСТ 1284.1-89, ГОСТ 1284.2-89, ГОСТ 1284.3-89). Стандартом предусмотрено 7 ремней нормального сечения (Z, A, B, C, D, E, E0), у которых b0/h»1,6, и 4 – узкого сечения (YZ, YA, YB, YC), у которых b0/h»1,25. Ремни изготавливаются в виде замкнутого кольца, поэтому их длина тоже стандартизована.
таким образом, ремень со шкивом образуют клиновую кинематическую пару, для которой приведенный коэффициент трения f* выражается зависимостью
где f – коэффициент трения между контактирующими поверхностями ремня и шкива, а j - угол между боковыми рабочими поверхностями ремня. После подстановки в (2.36) фактического значения угла j получаем, что f*=2,92 f, то есть при одном и том же диаметре ведущего шкива несущая способность клиноременной передачи будет примерно втрое выше по сравнению с плоскоременной. Поэтому, если в плоскоременных передачах рекомендуют угол охвата меньшего шкива a ³ 150°, то в клиноременных - a ³ 120° и допускается даже a = 75…80°. Последнее обстоятельство позволяет использовать 1 ремень для передачи вращательного движения от одного ведущего нескольким ведомым шкивам (например, в автомобильных ДВС используется ременный привод одним ремнем водяной помпы в системе охлаждения, электрогенератора и вентилятора). Проектный расчет клиноременных передач выполняется достаточно просто методом подбора, поскольку в стандартах указывается мощность, передаваемая одним ремнем при определенном расчетном диаметре меньшего шкива и известной средней скорости ремня или частоте вращения шкива. Изложенная лекция, как и предыдущая, состоит из двух частей, первая из которых посвящена общим вопросам проектирования механических передач. В этой части лекции представлены основные параметры, характеризующие всякую механическую передачу, и показана связь между ними. Во второй части лекции изложены теоретические основы расчета ременных передач, их геометрические, кинематические и силовые характеристики, представлены соотношения связывающие различные параметры ременных передач между собой. Более полные сведения о ременных передачах можно найти в учебной и технической литературе.
1. Какое устройство можно назвать механической передачей? 2. Какие основные параметры характеризуют механическую передачу? 3. В чем заключается разница между передаточным отношением и передаточным числом? 4. Что означает коэффициент полезного действия, коэффициент потерь, какова их сумма? 5. В чем разница между угловой скоростью и частотой вращения, в каких единицах они измеряются? 6. Как связаны скоростные и нагрузочные параметры прямолинейного и вращательного движения? 7. Как связаны тангенциальная сила и вращающий момент, ею создаваемый? 8. Что называют ременной передачей? 9. Какие виды ремней используются в ременных передачах? 10. Назовите основные геометрические параметры ременной передачи. 11. Каковы соотношения между силами натяжения ветвей ремня в ременной передаче - при неработающей передаче, в процессе работы? 12. Что характеризует коэффициент тяги ременной передачи? 13. Какие показатели ременной передачи непосредственно влияют на величину оптимального коэффициента тяги? 14. Что характеризует коэффициент скольжения ременной передачи? 15. Как определить точное значение передаточного числа ременной передачи? 16. Как меняется коэффициент скольжения и КПД с ростом коэффициента тяги? 17. Какие силы создают напряжения в ремне при работе ременной передачи? 18. Какие процессы, происходящие в ремне при работе передачи, ответственны за его усталостный износ? 19. Как выполняется проектный расчет плоскоременной передачи? 20. По какому критерию выполняется проверочный расчет ременной передачи? 21. Назовите основные особенности поперечного сечения клинового и поликлинового ремней? 22. Почему передача клиновым ремнем имеет большую несущую способность по сравнению с плоскоременной? 23. По каким критериям выполняется проектный расчет клиноременной передачи?
é
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 893; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.175.66 (0.015 с.) |

 и
и 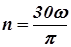 (2.1)
(2.1)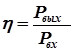 (2.2)
(2.2) (2.3)
(2.3)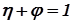 (2.4)
(2.4)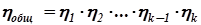 . (2.5)
. (2.5) . (2.6)
. (2.6)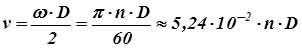 . (2.7)
. (2.7) . (2.8)
. (2.8) , (2.9)
, (2.9)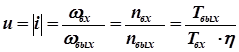 . (2.10)
. (2.10)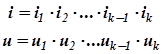 . (2.11)
. (2.11)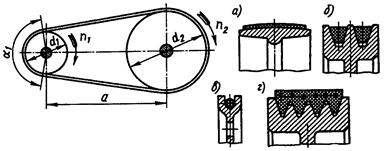 Рис. 2.1. Принципиальная схема ременной передачи и основные виды фрикционных ремней: а) плоский; б) клиновой; в) круглый; г) поликлиновой.
Рис. 2.1. Принципиальная схема ременной передачи и основные виды фрикционных ремней: а) плоский; б) клиновой; в) круглый; г) поликлиновой.
 Рис. 2.2. Геометрия открытой ременной передачи.
Рис. 2.2. Геометрия открытой ременной передачи.
 , (2.12)
, (2.12) . (2.13)
. (2.13) (2.14)
(2.14) (2.15)
(2.15) . (2.16)
. (2.16) . (2.17)
. (2.17) ,
, ,
,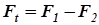 , но с другой стороны, как и для всякой передачи вращения
, но с другой стороны, как и для всякой передачи вращения  (см. (2.8)), а для поступательно движущихся ветвей ремня можно записать
(см. (2.8)), а для поступательно движущихся ветвей ремня можно записать  , где P – мощность передачи, а Vp средняя скорость движения ремня. Суммарное натяжение ветвей ремня остается неизменным, как в работающей, так и в неработающей передаче, то есть
, где P – мощность передачи, а Vp средняя скорость движения ремня. Суммарное натяжение ветвей ремня остается неизменным, как в работающей, так и в неработающей передаче, то есть  . Но по формуле Эйлера для ремня, охватывающего шкив,
. Но по формуле Эйлера для ремня, охватывающего шкив, 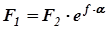 , где – основание натурального логарифма (e» 2,7183), f – коэффициент трения покоя (коэффициент сцепления) между материалами ремня и шкива (табл. 2.1), a – угол охвата ремнем шкива (определен выше).
, где – основание натурального логарифма (e» 2,7183), f – коэффициент трения покоя (коэффициент сцепления) между материалами ремня и шкива (табл. 2.1), a – угол охвата ремнем шкива (определен выше).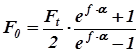 , (2.18)
, (2.18) , (2.19)
, (2.19) Рис. 2.3. Силы в ременной передаче.
Рис. 2.3. Силы в ременной передаче.
 . (2.20)
. (2.20)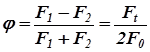 . (2.21)
. (2.21) . (2.22)
. (2.22) , (2.23)
, (2.23)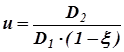 . (2.24)
. (2.24) Рис. 2.4. Кривые скольжения и КПД.
Рис. 2.4. Кривые скольжения и КПД.
 . (2.25)
. (2.25) , (2.26)
, (2.26) , (2.27)
, (2.27)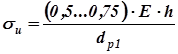 . (2.28)
. (2.28) , (2.29)
, (2.29) . (2.30)
. (2.30) . (2.31)
. (2.31) , (2.32)
, (2.32) ; (2.33)
; (2.33)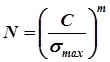 . (2.34)
. (2.34) при постоянном режиме нагружения и u» 1 (a = 180°), нетрудно получить выражение для определения срока службы ремня T0 в часах работы
при постоянном режиме нагружения и u» 1 (a = 180°), нетрудно получить выражение для определения срока службы ремня T0 в часах работы , (2.35)
, (2.35) Рис. 2.5. Размеры сечений клинового (а, б) и поликлинового (в) ремней
Рис. 2.5. Размеры сечений клинового (а, б) и поликлинового (в) ремней
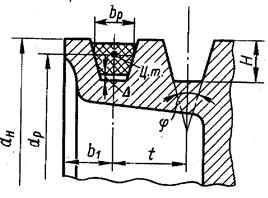 Рис. 2.6. Расположение клинового ремня в ручье шкива.
Рис. 2.6. Расположение клинового ремня в ручье шкива.
 , (2.36)
, (2.36)


