
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция № 4. Общие сведения о зубчатых передачах (ЗП)Содержание книги
Поиск на нашем сайте
Вопросы, изложенные в лекции: 5. Общие сведения. 6. Передачи с эвольвентным зацеплением. 7. Передачи с зацеплениями других типов.
Зубчатая передача - трехзвенный механизм, включающий два подвижных звена, взаимодействующих между собой через высшую зубчатую кинематическую пару и образующих с третьим неподвижным звеном низшие (вращательные или поступательные) кинематические пары (рис. 4.1).
Меньшее зубчатое колесо, участвующее в зацеплении обычно называют шестерней, большее – зубчатым колесом, звено зубчатой передачи, совершающее прямолинейное движение, называют зубчатой рейкой (рис. 4.1, к). Назначение зубчатой передачи - передача движения (чаще всего вращательного) с преобразованием параметров, а иногда и его вида (реечная передача). Зубчатые передачи вращательного движения наиболее распространены в технике (рис. 4.1, а…и). Они характеризуются передаваемыми мощностями от микроватт (механизм кварцевых наручных часов) до десятков тысяч киловатт (крупные шаровые мельницы, дробилки, обжиговые печи) при окружных скоростях до 150 м/с. Классификация зубчатых передач: 1. По величине передаточного числа: 1.1. с передаточным числом u ³ 1 – редуцирующие (редукторы - большинство зубчатых передач); 1.2. с передаточным числом u < 1 – мультиплицирующие (мультипликаторы). 2. По взаимному расположению валов: 2.1. с параллельными валами - цилиндрические зубчатые передачи (рис. 4.1, а…г); 2.2. с пересекающимися осями валов - конические зубчатые передачи (конические передачи с углом 90° между осями валов называют ортогональными; рис. 4.1, д…ж); 2.3. с перекрещивающимися осями валов - червячные, винтовые (рис. 4.1, и), гипоидные (рис. 4.1, з); 2.4. с преобразованием движения – реечные (рис. 4.1, к). 3. По расположению зубьев относительно образующей поверхности колеса: 3.1. прямозубые - продольная ось зуба параллельна образующей поверхности колеса (рис. 4.1, а, г, д, к); 3.2. косозубые - продольная ось зуба направлена под углом к образующей поверхности колеса (рис. 4.1, б, е, и); 3.3. шевронные - зуб выполнен в форме двух косозубых колес со встречным наклоном осей зубьев (рис. 4.1, в); 3.4. с круговым зубом - ось зуба выполнена по окружности относительно образующей поверхности колеса (рис. 4.1, ж, з). 4. По форме зацепляющихся звеньев: 4.1. с внешним зацеплением - зубья направлены своими вершинами от оси вращения колеса (рис. 4.1, а…в); 4.2. с внутренним зацеплением - зубья одного из зацепляющихся колес направлены своими вершинами к оси вращения колеса (рис. 4.1, г); 4.3. реечное зацепление - одно из колес заменено прямолинейной зубчатой рейкой (рис. 4.1, к); 4.4. с некруглыми колесами. 5. По форме рабочего профиля зуба: 5.1. эвольвентные - рабочий профиль зуба очерчен по эвольвенте круга (линия описываемая точкой прямой, катящейся без скольжения по окружности); 5.2. циклоидальные - рабочий профиль зуба очерчен по круговой циклоиде (линия описываемая точкой окружности, катящейся без скольжения по другой окружности); 5.3. цевочное (разновидность циклоидального) – зубья одного из колес, входящих в зацепление, заменены цилиндрическими пальцами – цевками; 5.4. с круговым профилем зуба (зацепление Новикова) – рабочие профили зубьев образованы дугами окружности практически одинаковых радиусов. 6. По относительной подвижности геометрических осей зубчатых колес: 6.1. с неподвижными осями колес - рядовые передачи (рис. 4.1); 6.2. с подвижными осями некоторых колес - планетарные передачи. 7. По жесткости зубчатого венца колес, входящих в зацепление: 7.1. с колесами неизменяемой формы (с жестким венцом); 7.2. включающая колеса с венцом изменяющейся формы (гибким). 8. По окружной (тангенциальной) скорости зубьев: 8.1. тихоходные (Vз < 3 м/с); 8.2. среднескоростные (3< Vз < 15 м/с); 8.3. быстроходные (Vз > 15 м/с). 9. По конструктивному исполнению: 9.1. открытые (бескорпусные); 9.2. закрытые (корпусные). Наиболее широкое применение находят редуцирующие зубчатые передачи вращательного движения, в том числе и в многоцелевых гусеничных и колесных машинах (коробки передач, бортовые редукторы, приводы различных устройств). Поэтому дальнейшее изложение, если это не упоминается особо, касается только передач вращательного движения. Достоинства зубчатых передач: 1. Высокая надежность работы в широком диапазоне нагрузок и скоростей. 2. Большой ресурс. 3. Малые габариты. 4 Высокий КПД. 5. Относительно малые нагрузки на валы и подшипники. 5. Постоянство предаточного числа. 6. Простота обслуживания. Недостатки зубчатых передач: 1. Сложность изготовления и ремонта (необходимо высокоточное специализированное оборудование). 2. Относительно высокий уровень шума, особенно на больших скоростях. 3. Нерациональное использование зубьев – в работе передачи одновременно участвуют обычно не более двух зубьев каждого из зацепляющихся колёс. Конструктивные (геометрические) параметры зубчатых передач (на примере цилиндрических зубчатых передач): Межосевое расстояние aw – расстояние между геометрическими осями валов, на которых закреплены шестерня и зубчатое колесо. Диаметры начальных цилиндров (окружностей) зубчатых колес dw1 и dw2 [1], участвующих в зацеплении – диаметры мнимых цилиндров (в сечении, перпендикулярном осям вращения взаимодействующих зубчатых колес, окружностей), которые в процессе работы передачи обкатываются один по другому без проскальзывания. При изменении межосевого расстояния передачи меняются и диаметры начальных цилиндров (окружностей). У отдельно взятого колеса диаметра начального цилиндра (окружности) не существует. Названные параметры передачи связаны между собой простым соотношением
где знак «+» относится к внешнему зацеплению (рис. 4.1, а…в, и), а знак «-» - к внутреннему (рис. 4.1, г). Числа зубьев зубчатых колес z1 и z2. Суммарное число зубьев колес, участвующих в передаче
Делительные диаметры d1 и d2 зубчатых колес, участвующих в зацеплении – диаметры цилиндров (окружностей) по которым обкатывается без скольжения инструмент при нарезании зубьев колеса методом обкатки. У большинства зубчатых передач (при отсутствии ошибок в изготовлении) делительные диаметры и диаметры начальных цилиндров совпадают, то есть dw1 = d1 и dw2 = d2. Поскольку делительные диаметры связаны с процессом изготовления зубчатого колеса, а каждое зубчатое колесо изготавливается отдельно, следовательно делительный диаметр (делительный цилиндр, в поперечном сечении – делительная окружность) имеется у каждого отдельно взятого колеса. Часть делительного диаметра, приходящаяся на один зуб колеса называется модулем m, следовательно для любого нормального зубчатого колеса
Модуль является основной размерной характеристикой зубьев колеса. С целью обеспечения взаимозаменяемости зубчатых колес, унификации и сокращения номенклатуры режущего инструмента для их изготовления модуль стандартизован, то есть при проектировании передачи выбирается из ряда стандартных значений. Расстояние между одноименными боковыми поверхностями двух соседних зубьев, измеренное по дуге делительной окружности называют окружным делительным шагом зубьев p. Так как длина делительной окружности равна p´d, то, учитывая (4.3), для любого зубчатого колеса имеем
Из сказанного следует, в зацеплении могут находиться только зубчатые колеса с одинаковым модулем. Кинематические параметры зубчатых передач: угловые скорости w1, w2 и частоты вращения n1, n2 ведущего и ведомого зубчатых колес, а также связанное с ними передаточное число зубчатой передачи, вычисляемое по соотношению
Учитывая вышеизложенное, нетрудно установить, что
Для нормальной работы зубчатой передачи (обеспечение плавности работы, отсутствие излишних вибраций и инерционных сил, относительно высокий КПД зубчатого зацепления) форма рабочей поверхности профиля зубьев должна удовлетворять следующим требованиям: 1. в течение времени взаимодействия рабочих поверхностей двух сопряженных зубьев ведущего и ведомого колес передаточное отношение должно сохраняться постоянным (основная теорема зубчатого зацепления); 2. профиль зуба должен обеспечивать выполнение условия 1 при зацеплении данного колеса с любым другим колесом того же модуля; 3. профиль зуба должен обеспечивать возможность изготовления колеса любого диаметра одним инструментом; 4. инструмент для нарезания зубьев должен быть простым и легко доступным для изготовления и контроля.
Наиболее полно перечисленным требованиям удовлетворяет эвольвентное зацепление, предложенное Леонардом Эйлером (в 1760 или 65 г.), которое и получило самое широкое распространение в общепромышленной и военной технике. [2] Основные параметры эвольвентных цилиндрических зубчатых передач стандартизованы, при обозначении параметрам шестерни приписывается индекс " 1 ", параметрам колеса - " 2 " (рис. 4.2):
1. Межосевая линия О1О2 - прямая линия, пересекающая оси зубчатых колес передачи под прямым углом. 2. Межосевое расстояние (аw) - расстояние между осями зубчатых колес О1 и О2, измеренное по межосевой линии. 3. Линия зацепления (NN) - геометрическое место точек контакта между сопряженными профилями зубьев. Линия зацепления одновременно является нормалью к профилю боковой (рабочей) поверхности зуба, и потому усилие нормального давления между зубьями всегда направлено по линии зацепления. 4. Угол зацепления (aw) - угол между линией зацепления и перпендикуляром к межосевой линии. (стандартный угол зацепления aw = 20°; уменьшенный угол зацепления aw = 15°; увеличенный - aw = 22,5°). 5. Основная окружность (основной цилиндр; его диаметры обозначаются db1 и db2, радиусы – rb1 и rb2) - окружность, по которой обкатывается без скольжения прямая, точки которой описывают эвольвенту, очерчивающую боковую поверхность зуба, следовательно это окружность с центром на оси вращения колеса, касающаяся линии зацепления. 6. Начальные окружности (начальный цилиндр; его диаметры обозначаются dw1, dw2) - окружности сопряженных зубчатых колес, которые при их вращении обкатываются одна по другой без проскальзывания. 7. Делительные окружности (делительные цилиндры их диаметры обозначаются d1, d2) – окружности зубчатых колес, при измерении по которым теоретические толщина зуба и ширина впадины равны между собой (окружности по которым обкатывается инструмент при нарезании зубьев). У некоррегированных зубчатых колес делительная и начальная окружности совпадают. 8. Окружность выступов (цилиндры выступов; их диаметры обозначаются da1, da2) – окружность, очерченная по вершинам зубьев. 9. Окружность впадин (цилиндры впадин; их диаметры обозначаются df1, df2)- окружность, очерченная по дну впадин между зубьями. 10. Шаг нарезки зубьев (р) – расстояние между одноименными точками боковой (рабочей) поверхности зубьев, измеренное по дуге окружности с центром на оси вращения колеса. В зависимости от окружности по которой измеряется шаг нарезки различают основной (рb) начальный (pw) и делительный (р1) шаги (см. формулу 4.4). 11. Модуль (т) – часть диаметра делительной окружности, приходящаяся на 1 зуб колеса (см. формулу 4.3). 12. Высота головки зуба (hа) – расстояние между делительной окружностью и окружностью выступов, измеренное по радиусу (обычно hа= т). 13. Высота ножки зуба (hf) – расстояние между делительной окружностью и окружностью впадин, измеренное по радиусу (обычно hf = 1,25×т для цилиндрических колес и hf = 1,20×т для конических колес). 14. Высота зуба (h) – расстояние между окружностью впадин и окружностью выступов, измеренное по радиусу. Высота зуба складывается из высот его ножки и головки (h = ha + hf, следовательно, для цилиндрических колес h = 2,25×т, а для конических h = 2,20×т). 15. Ширина зубчатого венца (b) – расстояние между торцовыми поверхностями зубчатого венца колеса. 16. Боковой зазор в зацеплении (j) – полуразность между толщиной зуба и шириной впадины, измеренными по дуге делительной окружности (обычно j = 0,0125m – для литых колес и j = (0…0,0065)m – для механически обработанных колес). 17. Угол наклона зубьев (b) – угол между продольной осью зуба и образующей поверхности зубчатого венца колеса (для прямозубых колес b =0 и, как правило, не указывается). 18. Радиальный зазор (с) – разница между высотой ножки и головки зуба (обычно с = 0,25×т для цилиндрических колес и с =0,20×т для конических колес). 19. Длина активной линии зацепления (ga)- часть линии зацепления, отсекаемая окружностями выступов сопрягаемых колес (на рис. 4.2 не показана). 20. Коэффициент торцового перекрытия (ea = ga /рь) - отношение длины активной линии зацепления к основному шагу колеса. Коэффициент торцового перекрытия показывает сколько зубьев в среднем за поворот колеса на 1 шаг находятся в зацеплении. Основные параметры эвольвентных конических зубчатых передач. Конические зубчатые эвольвентные передачи предназначены для передачи вращательного движения между валами, геометрические оси которых пересекаются. Наиболее часто угол между осями валов составляет 90°, передачи с таким углом принято называть ортогональными (рис. 4.3).
Зубья колес в конической передаче имеют переменные размеры сечения по длине, что обусловливает большую трудность изготовления (отсюда ниже точность) и меньшую несущую способность передачи (в среднем примерно на 15%). Конусная образующая поверхность зубчатого венца вызывает появление значительных осевых сил на валах передачи, что является причиной усложнения конструкции опор и всей передачи в целом. Конусы, аналогичные начальному и делительному цилиндрам цилиндрического колеса, называют начальным и делительным конусами. Угол между осью начального конуса и его образующей называют углом начального конуса (обозначают d1 – угол начального конуса ведущего колеса; d2 – угол начального конуса ведомого колеса). В некоррегированных передачах начальные и делительные конусы совпадают. Дополнительные конусы – конусы, образующая которых перпендикулярна образующей начального конуса. Обычно у зубчатого колеса имеется 2 дополнительных конуса – внешний, наиболее удаленный от точки пересечения осей колес и внутренний, расположенный ближе к этой точке. Ширина зубчатого венца конического колеса (b) – часть образующей делительного конуса колеса между дополнительными конусами. Сечение зубьев поверхностью дополнительного конуса называют торцевым сечением. Различают внешнее, среднее и внутреннее торцевые сечения. Для передач с прямыми и косыми зубьями стандартизуются и указываются в конструкторской документации обычно параметры, относящиеся к внешнему торцевому сечению, а в расчетах используются параметры, относящиеся к среднему (медиальному) торцевому сечению. Для передач с круговым зубом расчетные и конструктивные (в том числе стандартизованные) параметры относятся к среднему (медиальному) торцевому сечению. Расстояние от вершины делительного конуса до пересечения его образующей с образующей внешнего дополнительного конуса называют внешним конусным расстоянием (Rе), а расстояние от вершины делительного конуса до пересечения его образующей с образующей среднего (медиального) дополнительного конуса называют медиальным конусным расстоянием (R). Для сопряженных (находящихся в зацеплении) зубчатых колес Rе1= Rе2 и R1= R2. Эквивалентное цилиндрическое колесо получается при развертке внешнего дополнительного конуса на плоскость с дополнением полученной развертки до полной окружности. Делительный диаметр эквивалентного колеса с прямолинейными зубьями можно представить в следующем виде
откуда следует, что
Для передачи с круговыми зубьями эквивалентное число зубьев выразится зависимостью
где bm – угол наклона кругового зуба в медианальном сечении.
Циклоидальные и цевочные зацепления были известны примерно на 100 лет раньше эвольвентных. Циклоидальное зацепление – это зацепление, в котором боковые рабочие поверхности зубьев сопряженных колес очерчены по циклоиде. Циклоида - кривая, описываемая точкой окружности, катящейся без скольжения по другой окружности. При обкатывании производящей окружности по главной окружности с внешней стороны получаем эпициклоиду, а при обкатывании с внутренней стороны – гипоциклоиду. При этом производящая окружность обкатывается по делительной окружности зубчатого колеса, совпадающей в зацеплении с начальной окружностью. Для циклоидального зацепления выполняется основная теорема зацепления – нормаль в точке взаимодействия профилей сопряженных зубьев проходит через полюс зацепления. В циклоидальном зацеплении рабочий профиль головки зуба очерчен по эпициклоиде, а профиль ножки зуба по гипоциклоиде. Оба профиля образованы обкаткой производящих окружностей по начальным окружностям шестерни и колеса. Обычно принимают диаметр производящей окружности dпр = (0,35…0,4)d. В следствие этого циклоидальное зацепление по сравнению с эвольвентным более чувствительно к неточностям межосевого расстояния. В настоящее время зубчатые колеса циклоидального зацепления нарезают, как правило, по методу обкатки способом фрезерования червячной фрезой. При этом боковой профиль зуба червячной фрезы также состоит из двух ветвей – эпо- и гипоциклоиды. Достоинства циклоидального зацепления: 1) Пониженные по сравнению с эвольвентным зацеплением контактные напряжения на рабочих поверхностях зубьев, вследствие увеличения приведенного радиуса кривизны контактных поверхностей. 2) Уменьшенный коэффициент скольжения зубьев при одном и том же коэффициенте перекрытия e. 3) Повышенная плавность работы передачи вследствие увеличения коэффициента перекрытия зубьев. Преимущество циклоидального зацепления особенно заметно проявляется при их использовании в ускоряющих (мультиплицирующих) передачах. Применение циклоидального зацепления в таких передачах способствует более благоприятному расположению нагрузки, действующей на зубья (значительно меньше угол зацепления), следовательно выше их КПД. Недостатки циклоидального зацепления: 1) Сложность инструментального профиля (две циклоиды по сравнению с прямой у эвольвентного зацепления). 2) Высокая чувствительность к ошибкам в исполнении межосевого расстояния (нарушается постоянство передаточного числа). 3) Трудности ремонта передачи – при изготовлении заменяющего колеса необходимо точно знать размеры производящей окружности. В машиностроении циклоидальное зацепление находит применение в винтовых насосах и компрессорах, в счетчиках оборотов и некоторых других устройствах.
Частным случаем циклоидального зацепления является цевочное зацепление. В цевочном зацеплении радиус производящей окружности одного из колес выбирается равным радиусу начальной (полоидной) окружности (рис. 4.4). В этом случае гипоциклоидальный профиль зубьев ответного колеса обращается в точку, что позволяет зубья первого колеса выполнить в форме цилиндрических пальцев, называемых цевками, укрепленных между двумя дисками; второе колесо при этом выполняется как зубчатое. Преимуществом цевочного зацепления является возможность отказаться от фрезерования зубцов одного из колес – цевочного колеса. Кроме того, цевки можно сделать вращающимися, заменив трение скольжения между зубьями колес трением качения, что увеличивает КПД передачи. Цевочное зацепление может быть как внешним, так и внутренним. Цевочное зацепление применяется в зубчатых механизмах больших габаритов: в подъемно-транспортных механизмах, в механизмах поворота орудийных башен, в некоторых типах планетарных редукторов. Во всех этих механизмах цевочным выполняют большее колесо, что позволяет отказаться от крупногабаритных зубофрезерных станков. Кроме того, в военной технике цевочное зацепление широко применяется в гусеничных движителях МГКМ для зацепления ведущего колеса с гусеницей, обеспечивая равномерность движения гусеницы при равномерном вращении ведущего колеса и безударное взаимодействие цевок гусеничной цепи с его впадинами. Передачи с круговым профилем рабочей поверхности зуба – зацепление М.Л. Новикова. Передача с круговым профилем зуба предложена инженер-полковником академии им. Н.Е. Жуковского М.Л. Новиковым в 1954 году. В основу разработки этого зацепления Новиковым положены следующие соображения. Согласно формуле Герца максимальные контактные напряжения между поверхностями взаимодействующих зубьев
где q – удельное усилие по линии контакта зубьев, Н/м; Eпр – приведенный модуль упругости материалов, из которых изготовлены зубчатые венцы взаимодействующих колес, Н/м2; rпр – приведенный радиус кривизны контактирующих поверхностей зубьев, вычисляемый по соотношению
Из соотношения (4.10) следует, что снизить напряжения в области контакта рабочих поверхностей зубьев возможно только за счет увеличения приведенного радиуса кривизны контактирующих поверхностей rпр. В свою очередь, соотношение (4.11) показывает, что максимальное увеличение rпр достигается в том случае, когда в контакте находятся поверхности противоположной кривизны, выпуклой и вогнутой, с близкими по абсолютной величине радиусами кривизны. Но в этом случае сохранение постоянства передаточного отношения при радиальном смещении точки контакта по поверхности зуба становится невозможным (нарушается основная теорема зацепления). Следовательно, остается единственная возможность – сохранить постоянство положения точки контакта в радиальном направлении и обеспечить её перемещение при вращении сцепляющихся колес параллельно их осям вращения. В зацеплении Новикова профиль контактирующих зубьев шестерни и колеса в торцевом сечении очерчен дугами окружности (рис. 4.5, б). Практически принимают
При выполнении зуба ведущего колеса с вогнутым профилем (вращение левого колеса на рис. 4.5 против часовой стрелки) точка контакта зубьев всегда будет расположена перед полюсом зацепления, поэтому такое зацепление называют дополюсным. Если же профиль зуба ведущего колеса сделать выпуклым, а ведомого вогнутым (это соответствует вращению левого колеса на рис. 4.5 по часовой стрелке), то зуб ведущего колеса будет входить в контакт уже после прохождения полюса зацепления, такое зацепление называют заполюсным.
Зубья сопряженных колес, выполненные как показано на рис. 4.5, требуют для изготовления различного инструмента, что неудобно в производственных условиях. Поэтому было предложено зубья обоих взаимодействующих колес выполнять одинаковыми – головку зуба делать с выпуклым профилем, а ножку – с вогнутым (рис. 4.6). В этом случае зубья имеют две точки контакта, одна из которых расположена на головке зуба, а вторая на его ножке, которые к тому же расположены по разные стороны полюса зацепления. Поэтому такое зацепление принято называть дозаполюсным. В российской промышленности профиль дозаполюсного зацепления стандартизован (ГОСТ 17744-72). Для этого профиля ha = 0,9; c = 0,15; an = 27°; ra = 1,14…1,15; rf = 1,25…1,3. В следствие более высокой контактной прочности несущая способность круговинтовой передачи может до двух раз превышать несущую способность эвольвентной передачи тех же размеров. Передача Новикова работает более плавно, а её КПД из-за отсутствия взаимного скольжения зубьев несколько выше. К недостаткам передачи Новикова можно отнести повышенную чувствительность к колебаниям межосевого расстояния и некоторое снижение изломной прочности зубьев вблизи торцов зубчатого венца. Круговинтовое зацепление можно использовать как в цилиндрических так и в конических зубчатых передачах. В лекции представлены: основная терминология, относящаяся к зубчатым передачам, классификация зубчатых передач, их основные достоинства и недостатки, представлены наиболее общие параметры зубчатых передач и рассмотрены основные свойства различных зубчатых зацеплений, используемых в силовых зубчатых передачах. Поскольку эвольвентное зацепление занимает превалирующее место в современной технике, включая военную, его свойства, критерии проектирования и прочностного расчета будут рассмотрены в последующих лекциях. Однако, информация, полученная уже в этой лекции позволяет решать основной вопрос о выборе того или иного зацепления при проектировании передачи. Представленная информация достаточно важна и при назначении условий эксплуатации передач, если известно зацепление, примененное в данной конкретной передаче.
1. Какой механизм называют зубчатой передачей? 2. Назовите основные классификационные признаки зубчатых передач. 3. Назовите примеры применения зубчатых передач. 4. Назовите достоинства и недостатки зубчатых передач. 5. Назовите основные конструктивные параметры зубчатых передач, как они меж собой соотносятся? 6. Назовите основные кинематические параметры зубчатых передач, как они меж собой соотносятся? 7. В чем заключается главная особенность эвольвентных передач? 8. Назовите основные конструктивные параметры эвольвентных зубчатых передач, как они меж собой соотносятся? 9. Назовите основные кинематические параметры эвольвентных зубчатых передач, как они меж собой соотносятся? 10. Что называют конической зубчатой передачей? 11. Как различается несущая способность конической и цилиндрической передач? 12. Какае дополнительные параметры характерны для конических зубчатых передач? 13. Что означают термины «эквивалентное зубчатое колесо» и «эквивалентное число зубьев» по отношению к конической передаче? 14. Какое зацепление называют циклоидальным? 15. Каковы достоинства и недостатки циклоидального зацепления? 16. Какое зацепление называют цевочным, в чем его преимущества? 17. Где применяется цевочное зацепление? 18. Какова главная особенность зубчатого зацепления М.Л. Новикова? 19. Какое зацепление называют дополюсным, заполюсным, дозаполюсным? 20. Сравните несущую способность эвольвентного и круговинтового зацеплений, что является причиной различия в их несущей способности?
é
|
||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 134; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.214.139 (0.014 с.) |

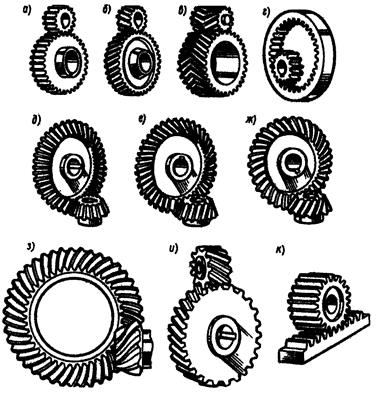 Рис. 4.1. Виды зубчатых передач.
Рис. 4.1. Виды зубчатых передач.
 , (4.1)
, (4.1) . (4.2)
. (4.2)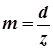 . (4.3)
. (4.3) . (4.4)
. (4.4)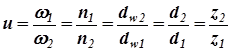 . (4.5)
. (4.5) . (4.6)
. (4.6) Рис. 4.2. Схема эвольвентного зацепления.
Рис. 4.2. Схема эвольвентного зацепления.
 Рис. 4.3. Схема зацепления ортогональной конической передачи: 1, 2, 3 – образующие внутреннего, среднего и внешнего дополнительных конусов; 4 - эквивалентное цилиндрическое колесо.
Рис. 4.3. Схема зацепления ортогональной конической передачи: 1, 2, 3 – образующие внутреннего, среднего и внешнего дополнительных конусов; 4 - эквивалентное цилиндрическое колесо.
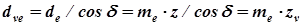 , (4.7)
, (4.7) . (4.8)
. (4.8)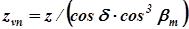 , (4.9)
, (4.9) Рис. 4.4. Схема построения цевочного зацепления.
Рис. 4.4. Схема построения цевочного зацепления.
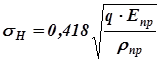 ; (4.10)
; (4.10) . (4.11)
. (4.11) , где r1 – радиус окружности вогнутого профиля зуба, а r2 – радиус окружности выпуклого профиля зуба, m – модуль зацепления. В этом случае контакт зубьев происходит в точке и только в момент прохождения профилей через эту точку. Для обеспечения перемещения точки контакта зубьев параллельно оси вращения шестерен зубья делают косыми с углом наклона обычно не более 25°. При этом ширину зацепления выбирают такой, чтобы обеспечивался осевой коэффициент перекрытия зубьев eb не менее 1,1, поскольку окружное перекрытие зубьев в таком зацеплении невозможно.
, где r1 – радиус окружности вогнутого профиля зуба, а r2 – радиус окружности выпуклого профиля зуба, m – модуль зацепления. В этом случае контакт зубьев происходит в точке и только в момент прохождения профилей через эту точку. Для обеспечения перемещения точки контакта зубьев параллельно оси вращения шестерен зубья делают косыми с углом наклона обычно не более 25°. При этом ширину зацепления выбирают такой, чтобы обеспечивался осевой коэффициент перекрытия зубьев eb не менее 1,1, поскольку окружное перекрытие зубьев в таком зацеплении невозможно. Рис. 4.5. Схема контактного взаимодействия и движения контактной площадки в зубчатом зацеплении: а) эвольвентном; б) круговинтовом (Новикова).
Рис. 4.5. Схема контактного взаимодействия и движения контактной площадки в зубчатом зацеплении: а) эвольвентном; б) круговинтовом (Новикова).
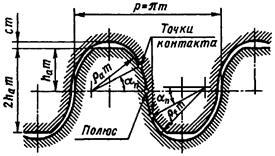 Рис. 4.6. Исходный контур дозаполюсной круговинтовой передачи (Новикова)
Рис. 4.6. Исходный контур дозаполюсной круговинтовой передачи (Новикова)



