
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача построение максимального потока. Связь с минимальными разрезами. Теорема Форда-Фалкерсона и теорема Менгера
§ Разрез графа — множество рёбер, удаление которых делит граф на два изолированных подграфа, один из которых, в частности, может быть отдельным узлом. § Разрез графа — линия, делящая граф на две несвязанные части. Теорема Форда—Фалкерсо́на — теорема о максимальном потоке в графе. Звучит так: величина максимального потока равна величине минимального разреза. Теорема Менгера о вершинной связности:
В теории оптимизации и теории графов, задача о максимальном потоке заключается в нахождении такого потока по транспортной сети, что сумма потоков из истока, или, что то же самое, сумма потоков в сток максимальна. Задача о максимальном потоке является частным случаем более трудных задач, как например задача о циркуляции. Дана транспортная сеть Величиной потока (value of flow) называется сумма потоков из источника Задача о максимальном потоке заключается в нахождении потока такого, что величина потока максимальна. 51. Алгоритм Форда-Фалкерсона.
Алгоритм проталкивания предпотока
Эйлеров цикл. Алгоритм построения. Построение эйлерова цикла Напомним, что эйлеровым циклом называется замкнутый маршрут, в котором каждое ребро графа встречается точно один раз. Согласно теореме 5 из лекции 2, для существования такого маршрута в связном графе необходимо и достаточно, чтобы степени всех вершин были четными. Теперь рассмотрим алгоритм, который находит эйлеров цикл в заданном графе при условии, что условия связности и четности степеней выполнены.
Этот алгоритм похож на алгоритм поиска в глубину: начиная с произвольно выбранной стартовой вершины Алгоритм 1. Построение эйлерова цикла
Для обоснования алгоритма заметим сначала, что первой в стек
Далее отметим, что в конечном итоге каждое ребро будет пройдено. Действительно, допустим, что в момент окончания работы алгоритма имеются еще не пройденные ребра. Поскольку граф связен, должно существовать хотя бы одно непройденное ребро, инцидентное посещенной вершине. Но тогда эта вершина не могла быть удалена из стека Будем говорить, что ребро При каждом повторении цикла while в рассмотренном алгоритме либо проходится одно ребро, либо одна вершина перемещается из
|
|||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 615; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.77.71 (0.01 с.) |


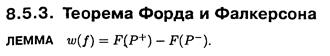
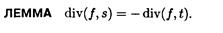
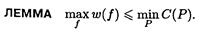
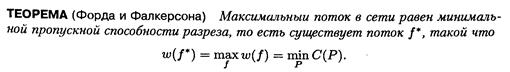
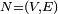 с источником
с источником  , стоком
, стоком 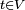 и пропускными способностями
и пропускными способностями  .
.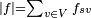 . В статье «Транспортная сеть» доказано, что она равна сумме потоков в сток
. В статье «Транспортная сеть» доказано, что она равна сумме потоков в сток 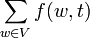 .
.
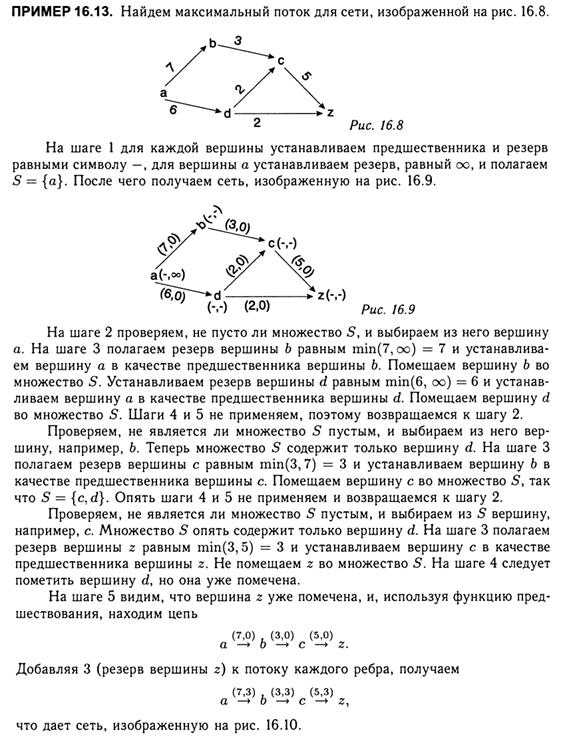









 , строим путь, выбирая каждый раз для дальнейшего продвижения еще не пройденное ребро. Главное отличие от поиска в глубину состоит в том, что как пройденные помечаются именно ребра, а не вершины. Поэтому одна и та же вершина может посещаться несколько раз, но каждое ребро проходится не более одного раза, так что в полученном маршруте ребра не будут повторяться. Вершины пути накапливаются в стеке
, строим путь, выбирая каждый раз для дальнейшего продвижения еще не пройденное ребро. Главное отличие от поиска в глубину состоит в том, что как пройденные помечаются именно ребра, а не вершины. Поэтому одна и та же вершина может посещаться несколько раз, но каждое ребро проходится не более одного раза, так что в полученном маршруте ребра не будут повторяться. Вершины пути накапливаются в стеке 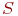 . Через некоторое количество шагов неизбежно наступит тупик - все ребра, инцидентные активной (последней посещенной) вершине
. Через некоторое количество шагов неизбежно наступит тупик - все ребра, инцидентные активной (последней посещенной) вершине  , уже пройдены. Так как степени всех вершин графа четны, в этот момент
, уже пройдены. Так как степени всех вершин графа четны, в этот момент  и пройденные ребра образуют цикл, но он может включать не все ребра графа. Для обнаружения еще не пройденных ребер возвращаемся по пройденному пути, перекладывая вершины из стека
и пройденные ребра образуют цикл, но он может включать не все ребра графа. Для обнаружения еще не пройденных ребер возвращаемся по пройденному пути, перекладывая вершины из стека  , пока не встретим вершину
, пока не встретим вершину 
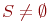 do
do 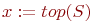
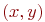

 . Ясно, что каждое ребро графа будет представлено в стеке
. Ясно, что каждое ребро графа будет представлено в стеке 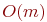 . Необходимо только оговориться, что этот вывод, как и аналогичные заключения об алгоритмах обхода в первых разделах этой главы, справедлив лишь при определенных предположениях о том, как задан граф. Способ задания должен обеспечить возможность быстрого просмотра множества ребер, инцидентных данной вершине. Подходящим является, например, задание графа списками инцидентности, в которых для каждой вершины перечисляются инцидентные ей ребра. Необходимо также иметь возможность быстро пометить ребро как пройденное или проверить, пройдено ли данное ребро. Для этого подходящей структурой может служить характеристический массив на множестве ребер.
. Необходимо только оговориться, что этот вывод, как и аналогичные заключения об алгоритмах обхода в первых разделах этой главы, справедлив лишь при определенных предположениях о том, как задан граф. Способ задания должен обеспечить возможность быстрого просмотра множества ребер, инцидентных данной вершине. Подходящим является, например, задание графа списками инцидентности, в которых для каждой вершины перечисляются инцидентные ей ребра. Необходимо также иметь возможность быстро пометить ребро как пройденное или проверить, пройдено ли данное ребро. Для этого подходящей структурой может служить характеристический массив на множестве ребер.


