Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Мощность Множеств. Равномощные множества. Конечные и бесконечныеСтр 1 из 10Следующая ⇒
Мощность Множеств. Равномощные множества. Конечные и бесконечные
Конечное множество состоит из конечного числа элементов, например, множество страниц в книге, множество учеников в школе и т.д. Бесконечное множество состоит из бесконечного числа элементов, т.е. это множество, которое не является ни конечным, ни пустым. Примеры: множество действительных чисел, множество точек плоскости, множество атомов во Вселенной и т.д.
Мощность множества. Добавление и удаление элементов. Вычисление мощности. Булеан
Число подмножеств конечного множества, состоящего из Операции над множествами. Диаграммы Венна. Разбиения и покрытия множеств
Свойства операций над множествами (не меньше 8)
6.Представление множеств в программах. Генерация всех подмножеств (2 способа)
7.Представление множеств упорядоченными списками. Проверка включения. Операция объединения и пересечения.
Отношения. Упорядоченные пары. Прямое произведение множеств.
9.Бинарные отношения. Основные определения и виды отношений. Композиция отношений.
Свойства отношений(6 штук). Представление отношений в компьютере.
Замыкание отношений. Алгоритм построения транзитивного замыкания.
Пусть на множестве
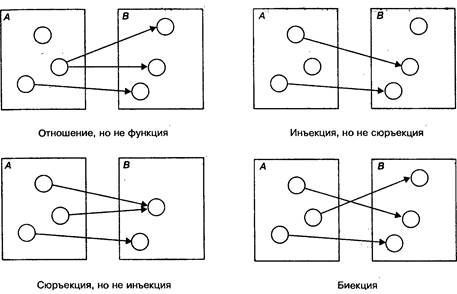
12.Функциональные отношения. Инъекция, сюрьекция и биекция.
13.Отношение эквивалентности. Классы эквивалентности.
Алгебра. Операции и носитель. Основные свойства операций(6 штук).
Алгебраическая система (или алгебраическая структура) в универсальной алгебре — множество
Морфизмы. Гомоморфизмы. Изоморфизмы.
Гомоморфизм - это отображение алгебраической системы А, сохраняющее основные операции и основные соотношения.
Например, рассмотрим группы
Пусть 1. 2. 17.Алгебры с одной операцией. Полугруппы. Моноиды Примеры § Целые числа с операцией сложения. § Положительные рациональные числа с операцией умножения. Произведение рациональных чисел — снова рациональное число, обратный элемент к рациональному числу представляется обратной дробью, имеется ассоциативность и единица. Простейшие свойства § Обратный к данному элемент всегда определяется однозначно. § (a −1)−1 = a, aman = am + n , (am) n = amn. § (ab)−1 = b −1 a −1. § Верны законы сокращения:
§ Обратный элемент к нейтральному есть сам нейтральный элемент. § Группа содержит единственное решение x любого уравнения x · c = b или c · x = b; то есть в группе возможны однозначно определённые правое и левое «деление». § Пересечение двух подгрупп группы G есть подгруппа группы G. § Теорема Лагранжа: если G — группа конечного порядка g, то порядок g 1 любой её подгруппы G 1 является делителем порядка группы. Из этого следует, что и порядок любого элемента делит порядок группы. § Для определения числа подгрупп в группе используются теорема Лагранжа и теоремы Силова.
Симметрической группой множества X называется группа всех перестановок X (то есть биекций X → X) относительно операции композиции. Симметрическая группа множества X обычно обозначается S (X). Если X = {1, 2,…, n }, то S (X) также обозначается через Sn. Нейтральным элементом в симметрической группе является тождественная перестановка
Свойства § При § При § В случае, если X конечно, число элементов S (X) равно n! (факториал n), где n — число элементов X. В частности, § Каждая конечная группа G изоморфна некоторой подгруппе группы S (G) (теорема Кэли).
§ Симметрическая группа Sn допускает следующее задание:
(Можно считать, что
Алгоритм построения СДНФ. СДНФ (Совершенная Дизъюнктивная Нормальная Форма) — это такая ДНФ, которая удовлетворяет трём условиям: § в ней нет одинаковых элементарных конъюнкций § в каждой конъюнкции нет одинаковых пропозициональных букв § каждая элементарная конъюнкция содержит каждую пропозициональную букву из входящих в данную ДНФ пропозициональных букв, причем в одинаковом порядке. Для любой функции алгебры логики существует своя СДНФ, причем единственная. Пример нахождения СДНФ Для того, чтобы получить СДНФ функции, требуется составить её таблицу истинности.
Первый столбец содержит 1 в указанном поле. Отмечаются значения всех четырёх переменных, это: § § § § Нулевые значения — тут все переменные представлены нулями — записываются в конечном выражении инверсией этой переменной. Первый член СДНФ рассматриваемой функции выглядит так: § § § §
Таким образом анализируются все ячейки Совершенная ДНФ этой функции:
Полнота системы булевых функций. Примеры полных систем.
Система булевых функций называется полной, если можно построить их суперпозицию, тождественную любой заранее заданной функции. Говорят ещё, что замыкание данной системы совпадает с множеством Теорема Поста. Замкнутые классы функций. Примеры.
Замкнутый класс в теории булевых функций — такое множество § Класс конъюнкций K, являющийся замыканием множества § Класс дизъюнкций D, являющийся замыканием множества По теореме Поста, чтобы система булевых функций была полной, надо, чтобы в ней существовали: 1. Хотя бы одна функция, не сохраняющая 0. 2. Хотя бы одна функция, не сохраняющая 1. 3. Хотя бы одна нелинейная функция. 4. Хотя бы одна немонотонная функция. 5. Хотя бы одна несамодвойственная функция. Этому требованию отвечает система функций
29.Определения теории графов. Смежность. Связность. Виды графов(ор-, псевдо- и т.д.).
Изоморфизм графов. Примеры
Связность Говорят, что две вершины связаны, если существует соединяющая их цепь. Граф, в котором все вершины связаны называется связным графом. Отношение того, что две вершены связаны – отношение эквивалентности на графе. Класс эквивалентности по отношению связности двух вершин называется компонентой связности графа. Число компонентов связности K(G) Если K == 1 => граф связный. Если K == 2 => граф не связный. Длина маршрута равна количеству ребер. Диаметр графа — это максимум расстояния между вершинами для всех пар вершин. Расстояние между вершинами — наименьшее число рёбер, которые необходимо пройти, чтобы добраться из одной вершины в другую.
Операции над графами 1. Дополнение графа
2. Объединение графов
3. Соединение графов
4. Добавление вершины
5. Удаление ребра
6. Удаление вершины
7. Стягивание подграфа A в G1(V1, E1)
8. Размножение вершины V
Поиск элемента (FIND) Дано: дерево Т и ключ K. Задача: проверить, есть ли узел с ключом K в дереве Т, и если да, то вернуть ссылку на этот узел. Алгоритм:
Удаление узла (REMOVE) Дано: дерево Т с корнем n и ключом K. Задача: удалить из дерева Т узел с ключом K (если такой есть). Алгоритм:
Обход дерева (TRAVERSE)
Есть три операции обхода узлов дерева, отличающиеся порядком обхода узлов. Первая операция — INFIX_TRAVERSE — позволяет обойти все узлы дерева в порядке возрастания ключей и применить к каждому узлу заданную пользователем функцию обратного вызова f. Эта функция обычно работает только с парой (K,V), хранящейся в узле. Операция INFIX_TRAVERSE реализуется рекурсивным образом: сначала она запускает себя для левого поддерева, потом запускает данную функцию для корня, потом запускает себя для правого поддерева.
INFIX_TRAVERSE: Дано: дерево Т и функция f Задача: применить f ко всем узлам дерева Т в порядке возрастания ключей Алгоритм:
В простейшем случае, функция f может выводить значение пары (K,V). При использовании операции INFIX_TRAVERSE будут выведены все пары в порядке возрастания ключей. Если же использовать PREFIX_TRAVERSE, то пары будут выведены в порядке, соответствующим описанию дерева, приведённого в начале статьи.
АВЛдеревья.Балансировка
Так называемые AVL-деревья (названные в честь их двух изобретателей Г.М. Адельсона-Вельского и Е.М. Ландиса) хранят дополнительно в каждой вершине разность между высотами левого и правого поддеревьев, которая в сбалансированном дереве может принимать только три значения: -1, 0, 1. Новая вершина добавляется как терминальная. После этого выполняется процедура восстановления балансировки. В ней используются следующие элементарные преобразования дерева, сохраняющие упорядоченность вершин:
Здесь вершина x поддерева, которая является его корнем, опускается вниз и влево. Бывший правый сын d вершины x становится новым корнем поддерева, а x становится левым сыном d. (Вершины x и d, начальник и подчиненный, как бы меняются ролями: бывший начальник становится подчиненным.) Поддерево c, которое было левым сыном вершины d, переходит в подчинение от вершины d к вершине x и становится ее правым сыном. Отметим, что упорядоченность вершин сохраняется: a < b < c< d < e. Таким образом, для выполнения преобразования надо лишь заменить фиксированное количество указателей в вершинах x, d, c и, возможно, в родительской для x вершине;
Здесь вершина x опускается вниз и вправо, ее бывший левый сын b становится новым корнем поддерева, а x — его правым сыном. Поддерево c переходит в подчинение от b к x. Операции вращения носят локальный характер и позволяют при необходимости исправить баланс поддерева с корнем x. Например, для восстановления баланса дерева, показанного на следующем рисунке, достаточно выполнить одно вращение вершины b влево:
В случае AVL-деревьев операции вращения повторяются в цикле при восстановлении баланса после добавления или удаления элемента, число вращений не превышает С x h, где h — высота дерева, C — константа.
Алгоритм Краскала Идея алгоритма. Искомые ребра соединяют вершины. Поэтому возможны две стратегии построения. Можно идти от вершин и для каждой из них искать минимальное ребро (как это сделано в алгоритме Прима) а можно для каждого ребра выяснять можно ли его включить в строящееся дерево. Алгоритм Краскала предлагает делать это следующим образом. Во-первых, ребра графа пронумеровываем в порядке возрастания весов. Затем для каждого ребра начиная с первого проверяем соединяет или нет оно две несвязные вершины, если да, то его можно включить в остовное дерево. Ясно, что если мы имеем V вершин, то работа алгоритма начинается с V несвязных компонент графа (пока из графа все ребра исключаем). Для того, чтобы их связать необходимо найти V-1 ребро. Другими словами, алгоритм организует процесс роста компонент связности в процессе которого он объединяются друг с другом до тех пор пока не останется одна являющаяся конечным результатом. Пример
Алгоритм Прима Сам алгоритм имеет очень простой вид. Искомый минимальный остов строится постепенно, добавлением в него рёбер по одному. Изначально остов полагается состоящим из единственной вершины (её можно выбрать произвольно). Затем выбирается ребро минимального веса, исходящее из этой вершины, и добавляется в минимальный остов. После этого остов содержит уже две вершины, и теперь ищется и добавляется ребро минимального веса, имеющее один конец в одной из двух выбранных вершин, а другой — наоборот, во всех остальных, кроме этих двух. И так далее, т.е. всякий раз ищется минимальное по весу ребро, один конец которого — уже взятая в остов вершина, а другой конец — ещё не взятая, и это ребро добавляется в остов (если таких рёбер несколько, можно взять любое). Этот процесс повторяется до тех пор, пока остов не станет содержать все вершины (или, что то же самое, В итоге будет построен остов, являющийся минимальным. Если граф был изначально не связен, то остов найден не будет (количество выбранных рёбер останется меньше
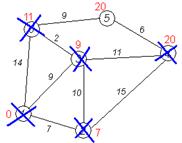
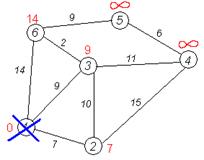
Формальное определение Дан взвешенный ориентированный[1] граф Неформальное объяснение Каждой вершине из V сопоставим метку — минимальное известное расстояние от этой вершины до a. Алгоритм работает пошагово — на каждом шаге он «посещает» одну вершину и пытается уменьшать метки. Работа алгоритма завершается, когда все вершины посещены. Инициализация. Метка самой вершины a полагается равной 0, метки остальных вершин — бесконечности. Это отражает то, что расстояния от a до других вершин пока неизвестны. Все вершины графа помечаются как непосещённые. Шаг алгоритма. Если все вершины посещены, алгоритм завершается. В противном случае, из ещё не посещённых вершин выбирается вершина u, имеющая минимальную метку. Мы рассматриваем всевозможные маршруты, в которых u является предпоследним пунктом. Вершины, в которые ведут рёбра из u, назовем соседями этой вершины. Для каждого соседа вершины u, кроме отмеченных как посещённые, рассмотрим новую длину пути, равную сумме значений текущей метки u и длины ребра, соединяющего u с этим соседом. Если полученное значение длины меньше значения метки соседа, заменим значение метки полученным значением длины. Рассмотрев всех соседей, пометим вершину u как посещенную и повторимшаг алгоритма. Пример Рассмотрим выполнение алгоритма на примере графа, показанного на рисунке. Пусть требуется найти кратчайшие расстояния от 1-й вершины до всех остальных.
Кружками обозначены вершины, линиями — пути между ними (ребра графа). В кружках обозначены номера вершин, над ребрами обозначена их «цена» — длина пути. Рядом с каждой вершиной красным обозначена метка — длина кратчайшего пути в эту вершину из вершины 1.
Первый шаг. Рассмотрим шаг алгоритма Дейкстры для нашего примера. Минимальную метку имеет вершина 1. Её соседями являются вершины 2, 3 и 6.
Первый по очереди сосед вершины 1 — вершина 2, потому что длина пути до неё минимальна. Длина пути в неё через вершину 1 равна сумме кратчайшего расстояния до вершины 1, значению её метки, и длины ребра, идущего из 1-й в 2-ю, то есть 0 + 7 = 7. Это меньше текущей метки вершины 2, бесконечности, поэтому новая метка 2-й вершины равна 7.
Аналогичную операцию проделываем с двумя другими соседями 1-й вершины — 3-й и 6-й.
Все соседи вершины 1 проверены. Текущее минимальное расстояние до вершины 1 считается окончательным и пересмотру не подлежит (то, что это действительно так, впервые доказал Э. Дейкстра). Вычеркнем её из графа, чтобы отметить, что эта вершина посещена.
Второй шаг. Шаг алгоритма повторяется. Снова находим «ближайшую» из непосещенных вершин. Это вершина 2 с меткой 7.
Снова пытаемся уменьшить метки соседей выбранной вершины, пытаясь пройти в них через 2-ю вершину. Соседями вершины 2 являются вершины 1, 3 и 4. Первый (по порядку) сосед вершины 2 — вершина 1. Но она уже посещена, поэтому с 1-й вершиной ничего не делаем. Следующий сосед вершины 2 — вершина 3, так как имеет минимальную метку из вершин, отмеченных как не посещённые. Если идти в неё через 2, то длина такого пути будет равна 17 (7 + 10 = 17). Но текущая метка третьей вершины равна 9<17, поэтому метка не меняется.
Все соседи вершины 2 просмотрены, замораживаем расстояние до неё и помечаем её как посещенную.
Третий шаг. Повторяем шаг алгоритма, выбрав вершину 3. После её «обработки» получим такие результаты:
Дальнейшие шаги. Повторяем шаг алгоритма для оставшихся вершин. Это будут вершины 6, 4 и 5, соответственно порядку.
Завершение выполнения алгоритма. Алгоритм заканчивает работу, когда нельзя больше обработать ни одной вершины. В данном примере все вершины зачеркнуты, однако ошибочно полагать, что так будет в любом примере - некоторые вершины могут остаться незачеркнутыми, если до них нельзя добраться. Результат работы алгоритма виден на последнем рисунке: кратчайший путь от вершины 1 до 2-й составляет 7, до 3-й — 9, до 4-й — 20, до 5-й — 20, до 6-й — 11.
АлгоритмА-star
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 350; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.119.199 (0.144 с.) |


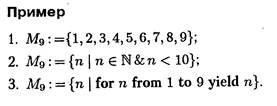



 элементов, равно
элементов, равно  .
.




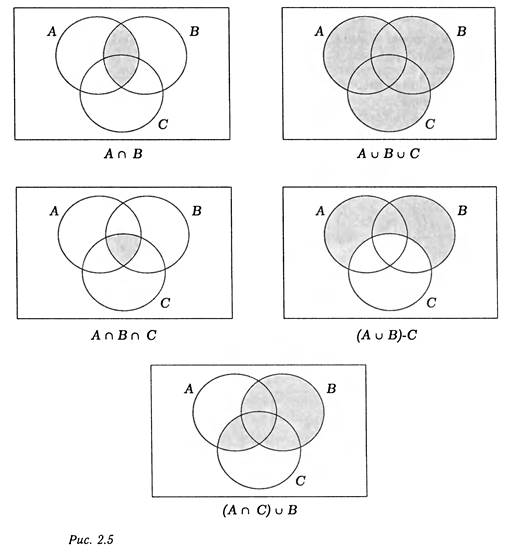



























 задано отношение
задано отношение  . Видно, что отношение
. Видно, что отношение  не симметрично, не рефлексивно и не транзитивно. Замыканием
не симметрично, не рефлексивно и не транзитивно. Замыканием  . Замыканием
. Замыканием  . Замыканием
. Замыканием  .
. 




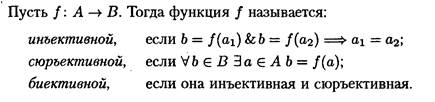



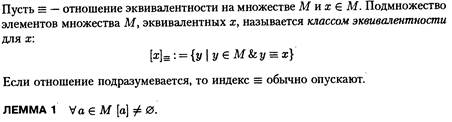
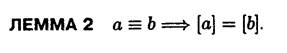




 (носитель) с заданным на нём набором операций и отношений (сигнатура), удовлетворяющим некоторой системе аксиом. Алгебраическая система с пустым множеством отношений называется универсальной алгеброй, а система с пустым множеством операций — моделью.
(носитель) с заданным на нём набором операций и отношений (сигнатура), удовлетворяющим некоторой системе аксиом. Алгебраическая система с пустым множеством отношений называется универсальной алгеброй, а система с пустым множеством операций — моделью.


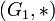 ,
, 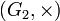 . Отображение
. Отображение  называется гомоморфизмом групп
называется гомоморфизмом групп  и
и  , если оно одну групповую операцию переводит в другую:
, если оно одну групповую операцию переводит в другую:  .
.

 и
и 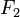 — поля. Биекция
— поля. Биекция 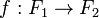 называется изоморфизмом, если для любых
называется изоморфизмом, если для любых  выполняется
выполняется ,
,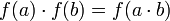 .
.


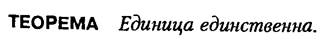

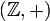 группа с нейтральным элементом 0. Она является абелевой.
группа с нейтральным элементом 0. Она является абелевой. ,
, .
. , определяемая как тождественное отображение:
, определяемая как тождественное отображение: для всех x из X.
для всех x из X. симметрическая группа Sn некоммутативна.
симметрическая группа Sn некоммутативна. симметрическая группа Sn является неразрешимой (и напротив: при
симметрическая группа Sn является неразрешимой (и напротив: при  — разрешимой).
— разрешимой).

 переставляет i и i +1.)
переставляет i и i +1.)

















 .
.

 функций алгебры логики, замыкание которого относительно операции суперпозиции совпадает с ним самим:
функций алгебры логики, замыкание которого относительно операции суперпозиции совпадает с ним самим: 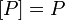 . Другими словами, любая функция, которую можно выразить формулой с использованием функций множества
. Другими словами, любая функция, которую можно выразить формулой с использованием функций множества  . Он представляет собой множество функций вида
. Он представляет собой множество функций вида  .
. . Он представляет собой множество функций вида
. Он представляет собой множество функций вида  .
. . На её основе и строятся полиномы Жегалкина.
. На её основе и строятся полиномы Жегалкина.













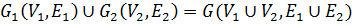




 \
\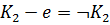




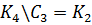
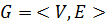




















 ребро).
ребро).







 без петель и дуг отрицательного веса[2]. Найти кратчайшие пути от некоторой вершины
без петель и дуг отрицательного веса[2]. Найти кратчайшие пути от некоторой вершины  графа
графа 





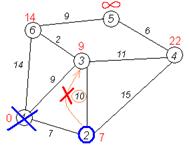
 , устанавливаем метку вершины 4 равной 22.
, устанавливаем метку вершины 4 равной 22.