
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гамильтонов цикл. Задача коммивояжера. ⇐ ПредыдущаяСтр 10 из 10
Гамильтоновы пути и циклы Гамильтоновым циклом (путем) называют простой цикл (путь), содержащий все вершины графа. В графе, изображенном на рис. 8.1 слева, гамильтоновым циклом является, например, последовательность
Внешне определение гамильтонова цикла похоже на определение эйлерова цикла. Однако есть кардинальное различие в сложности решения соответствующих задач распознавания и построения. Мы видели, что имеется достаточно простой критерий существования эйлерова цикла и эффективный алгоритм его построения. Для гамильтоновых же циклов (и путей) неизвестно никаких просто проверяемых необходимых и достаточных условий их существования, а все известные алгоритмы требуют для некоторых графов перебора большого числа вариантов. Гамильтонов цикл представляет собой, с комбинаторной точки зрения, просто перестановку вершин графа. При этом в качестве начальной вершины цикла можно выбрать любую вершину, так что можно рассматривать перестановки с фиксированным первым элементом. Самый бесхитростный план поиска гамильтонова цикла состоит в последовательном рассмотрении всех этих перестановок и проверке для каждой из них, представляет ли она цикл в данном графе. Такой способ действий уже при не очень большом числе вершин становится практически неосуществимым ввиду быстрого роста числа перестановок - имеется Более рациональный подход состоит в рассмотрении всевозможных простых путей, начинающихся в произвольно выбранной стартовой вершине Рассмотрим этот алгоритм подробнее. Будем считать, что граф задан окрестностями вершин: для каждой вершины
Алгоритм 2. Поиск гамильтоновых циклов
Этот алгоритм очень похож на алгоритм поиска в глубину и отличается от него по существу только тем, что открытая вершина, когда вся ее окрестность исследована, не закрывается, а опять становится новой (исключается из стека). В начале все вершины новые. Процесс заканчивается, когда все вершины опять станут новыми. На самом деле это и есть поиск в глубину, только не в самом графе, а в дереве путей. Вершинами этого дерева являются всевозможные простые пути, начинающиеся в вершине
В худшем случае время работы этого алгоритма тоже растет с факториальной скоростью. Например, для графа
Рассмотрим другой алгоритм, выясняющий существование гамильтонова цикла, по сути близкий к поиску в ширину и имеющий не столь быстро (хотя все же быстро) растущую оценку трудоемкости. Пусть граф
а для
Таким образом, зная все значения функции
После того, как будет вычислена функция
55. Раскраска графов. Хроматическое число. Алгоритм раскрашивания
56. Планарные графы. Задача укладки графа на поверхность. Примеры планарных графов.
Укладка на поверхности Пусть σ — произвольная поверхность в трехмерном пространстве. Граф G, изображенный на поверхности σ, называется уложенным на σ, если его ребра не пересекаются в точках, отличных от вершин. Граф G укладывается на поверхности σ, если он изоморфен некоторому графу, уложенному на σ. Свойство графа укладываться на поверхности безусловно зависит от вида этой поверхности. Однако многие поверхности с точки зрения укладки графов ничем не отличаются от плоскости. Принципиально важен следующий случай.
|
|||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 392; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.115.120 (0.02 с.) |
 ,
,  ,
, 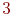 ,
, 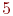 ,
, 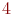 ,
,  . В правом графе нет и гамильтоновых путей.
. В правом графе нет и гамильтоновых путей.
 ! перестановок из
! перестановок из  элементов с фиксированным первым элементом.
элементов с фиксированным первым элементом. , до тех пор, пока не будет обнаружен гамильтонов цикл или все возможные пути не будут исследованы. По сути дела, речь тоже идет о переборе перестановок, но значительно сокращенном - если, например, вершина
, до тех пор, пока не будет обнаружен гамильтонов цикл или все возможные пути не будут исследованы. По сути дела, речь тоже идет о переборе перестановок, но значительно сокращенном - если, например, вершина  не смежна с вершиной
не смежна с вершиной  ! перестановок, у которых на первом месте стоит
! перестановок, у которых на первом месте стоит  задано множество вершин, смежных с
задано множество вершин, смежных с  всех вершин, смежных с
всех вершин, смежных с  . В дальнейшем рассмотренные вершины удаляются из этого множества. Очередной шаг состоит в исследовании окрестности последней вершины
. В дальнейшем рассмотренные вершины удаляются из этого множества. Очередной шаг состоит в исследовании окрестности последней вершины  и в
и в 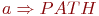
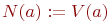
 do
do 


 не находится в PATH
не находится в PATH 


 (граф с двумя компонентами связности, одна из которых - полный граф с
(граф с двумя компонентами связности, одна из которых - полный граф с  вершиной, другая - изолированная вершина), если в качестве стартовой выбрана не изолированная вершина, то будут рассмотрены все
вершиной, другая - изолированная вершина), если в качестве стартовой выбрана не изолированная вершина, то будут рассмотрены все  простых путей длины
простых путей длины  в большой компоненте. Вместе с тем, если перед поиском гамильтонова цикла исходный граф проверить на связность, то ответ будет получен быстро. Можно пойти дальше и при обходе дерева путей поверять на связность каждый встречающийся "остаточный граф", т.е. граф, получающийся из исходного удалением всех вершин рассматриваемого пути. Если этот граф несвязен, то этот путь не может быть продолжен до гамильтонова пути. Поэтому можно не исследовать соответствующую ветвь дерева, а вернуться к рассмотрению более короткого пути, удалив последнюю вершину (т.е. сделать "шаг назад" в поиске в глубину). Можно пойти еще дальше и заметить, что если некоторая вершина
в большой компоненте. Вместе с тем, если перед поиском гамильтонова цикла исходный граф проверить на связность, то ответ будет получен быстро. Можно пойти дальше и при обходе дерева путей поверять на связность каждый встречающийся "остаточный граф", т.е. граф, получающийся из исходного удалением всех вершин рассматриваемого пути. Если этот граф несвязен, то этот путь не может быть продолжен до гамильтонова пути. Поэтому можно не исследовать соответствующую ветвь дерева, а вернуться к рассмотрению более короткого пути, удалив последнюю вершину (т.е. сделать "шаг назад" в поиске в глубину). Можно пойти еще дальше и заметить, что если некоторая вершина  задан матрицей смежности
задан матрицей смежности  . Выберем произвольно стартовую вершину
. Выберем произвольно стартовую вершину  функцию
функцию  , где значениями переменной
, где значениями переменной  -
-  -элементные подмножества множества
-элементные подмножества множества  , причем вершина
, причем вершина  , если существует простой путь длины
, если существует простой путь длины  из вершины
из вершины  , если такого пути не существует. Тогда
, если такого пути не существует. Тогда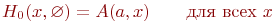 ,
,

 , мы можем вычислить все значения функции
, мы можем вычислить все значения функции  , причем для вычисления одного значения требуется выполнить
, причем для вычисления одного значения требуется выполнить  логических операций. Общее количество логических операций для вычисления всех этих функций составит
логических операций. Общее количество логических операций для вычисления всех этих функций составит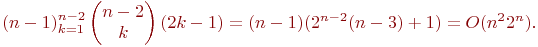
 , останется только для всех
, останется только для всех  (
(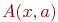 - если хотя бы в одном случае это 1, то гамильтонов цикл существует. Очевидный недостаток данного алгоритма - необходимость хранения большого количества промежуточной информации.
- если хотя бы в одном случае это 1, то гамильтонов цикл существует. Очевидный недостаток данного алгоритма - необходимость хранения большого количества промежуточной информации.














