Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ЗадачаНахожденияКратчайшегоПутиНаГрафе.АлгоритмБеллманаФорда
Алгоритм Беллмана–Форда — алгоритм поиска кратчайшего пути во взвешенном графе. В отличие от алгоритма Дейкстры, алгоритм Беллмана–Форда допускает рёбра с отрицательным весом. Граф с отрицательными циклами Алгоритм Беллмана–Форда позволяет очень просто определить, существует ли в графе G отрицательный цикл, достижимый из вершины s. Достаточно произвести внешнюю итерацию цикла не
ПРИМЕР: Выполнение алгоритма Беллмана-Форда: На рисунке в вершинах графа показаны значения атрибутов d на каждом этапе работы алгоритма, а выделенные ребра указывают на значения предшественников: если ребро (u, v) выделено, то prev[v] = u. В рассматриваемом примере при каждом проходе ребра ослабляются в следующем порядке: (t, х), (t, у), (t, z), (x,t), (у,х), (у, z), (z,x), (z,s), (s,t), (s,y). В части а рисунка показана ситуация, сложившаяся непосредственно перед первым проходом по ребрам. В частях б-д проиллюстрирована ситуация после каждого очередного прохода по ребрам. Значения атрибутов d и prev, приведенные в части д, являются окончательными.
46.Алгори́тм Де́йкстры Алгори́тм Де́йкстры (Dijkstra’s algorithm) — алгоритм на графах, изобретённый нидерландским ученым Э. Дейкстрой в 1959 году. Находит кратчайшее расстояние от одной из вершин графа до всех остальных Формальное определение Дан взвешенный ориентированный[1] граф Неформальное объяснение Каждой вершине из V сопоставим метку — минимальное известное расстояние от этой вершины до a. Алгоритм работает пошагово — на каждом шаге он «посещает» одну вершину и пытается уменьшать метки. Работа алгоритма завершается, когда все вершины посещены. Инициализация. Метка самой вершины a полагается равной 0, метки остальных вершин — бесконечности. Это отражает то, что расстояния от a до других вершин пока неизвестны. Все вершины графа помечаются как непосещённые.
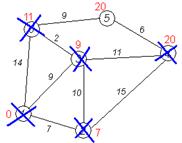
Шаг алгоритма. Если все вершины посещены, алгоритм завершается. В противном случае, из ещё не посещённых вершин выбирается вершина u, имеющая минимальную метку. Мы рассматриваем всевозможные маршруты, в которых u является предпоследним пунктом. Вершины, в которые ведут рёбра из u, назовем соседями этой вершины. Для каждого соседа вершины u, кроме отмеченных как посещённые, рассмотрим новую длину пути, равную сумме значений текущей метки u и длины ребра, соединяющего u с этим соседом. Если полученное значение длины меньше значения метки соседа, заменим значение метки полученным значением длины. Рассмотрев всех соседей, пометим вершину u как посещенную и повторимшаг алгоритма. Пример Рассмотрим выполнение алгоритма на примере графа, показанного на рисунке. Пусть требуется найти кратчайшие расстояния от 1-й вершины до всех остальных.
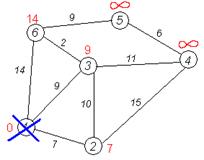
Кружками обозначены вершины, линиями — пути между ними (ребра графа). В кружках обозначены номера вершин, над ребрами обозначена их «цена» — длина пути. Рядом с каждой вершиной красным обозначена метка — длина кратчайшего пути в эту вершину из вершины 1.
Первый шаг. Рассмотрим шаг алгоритма Дейкстры для нашего примера. Минимальную метку имеет вершина 1. Её соседями являются вершины 2, 3 и 6.
Первый по очереди сосед вершины 1 — вершина 2, потому что длина пути до неё минимальна. Длина пути в неё через вершину 1 равна сумме кратчайшего расстояния до вершины 1, значению её метки, и длины ребра, идущего из 1-й в 2-ю, то есть 0 + 7 = 7. Это меньше текущей метки вершины 2, бесконечности, поэтому новая метка 2-й вершины равна 7.
Аналогичную операцию проделываем с двумя другими соседями 1-й вершины — 3-й и 6-й.
Все соседи вершины 1 проверены. Текущее минимальное расстояние до вершины 1 считается окончательным и пересмотру не подлежит (то, что это действительно так, впервые доказал Э. Дейкстра). Вычеркнем её из графа, чтобы отметить, что эта вершина посещена.
Второй шаг. Шаг алгоритма повторяется. Снова находим «ближайшую» из непосещенных вершин. Это вершина 2 с меткой 7.
Снова пытаемся уменьшить метки соседей выбранной вершины, пытаясь пройти в них через 2-ю вершину. Соседями вершины 2 являются вершины 1, 3 и 4. Первый (по порядку) сосед вершины 2 — вершина 1. Но она уже посещена, поэтому с 1-й вершиной ничего не делаем. Следующий сосед вершины 2 — вершина 3, так как имеет минимальную метку из вершин, отмеченных как не посещённые. Если идти в неё через 2, то длина такого пути будет равна 17 (7 + 10 = 17). Но текущая метка третьей вершины равна 9<17, поэтому метка не меняется.
Все соседи вершины 2 просмотрены, замораживаем расстояние до неё и помечаем её как посещенную.
Третий шаг. Повторяем шаг алгоритма, выбрав вершину 3. После её «обработки» получим такие результаты:
Дальнейшие шаги. Повторяем шаг алгоритма для оставшихся вершин. Это будут вершины 6, 4 и 5, соответственно порядку.
Завершение выполнения алгоритма. Алгоритм заканчивает работу, когда нельзя больше обработать ни одной вершины. В данном примере все вершины зачеркнуты, однако ошибочно полагать, что так будет в любом примере - некоторые вершины могут остаться незачеркнутыми, если до них нельзя добраться. Результат работы алгоритма виден на последнем рисунке: кратчайший путь от вершины 1 до 2-й составляет 7, до 3-й — 9, до 4-й — 20, до 5-й — 20, до 6-й — 11.
АлгоритмА-star A* пошагово просматривает все пути, ведущие от начальной вершины в конечную, пока не найдёт минимальный. Как и всеинформированные алгоритмы поиска, он просматривает сначала те маршруты, которые «кажутся» ведущими к цели. От жадного алгоритма (который тоже является алгоритмом поиска по первому лучшему совпадению) его отличает то, что при выборе вершины он учитывает, помимо прочего, весь пройденный до неё путь (составляющая g(x) — это стоимость пути от начальной вершины, а не от предыдущей, как в жадном алгоритме). В начале работы просматриваются узлы, смежные с начальным; выбирается тот из них, который имеет минимальное значение f(x), после чего этот узел раскрывается. На каждом этапе алгоритм оперирует с множеством путей из начальной точки до всех ещё не раскрытых (листовых) вершин графа («множеством частных решений»), которое размещается в очереди с приоритетом. Приоритет пути определяется по значению f(x) = g(x) + h(x). Алгоритм продолжает свою работу до тех пор, пока значение f(x) целевой вершины не окажется меньшим, чем любое значение в очереди (либо пока всё дерево не будет просмотрено). Из множественных решений выбирается решение с наименьшей стоимостью. Чем меньше эвристика h(x), тем больше приоритет (поэтому для реализации очереди можно использовать сортирующие деревья). Пример Примером алгоритма A* в действии, где узлы – это города, связанные дорогами и Н (х) является самым коротким расстоянием до целевой точки:
Ключ: зеленый - начало, синий - цель, оранжевый - посещенные узлы. Примечание: Этот пример использует запятую как десятичный разделитель.
48. Алгоритм Флойда-Уоршалла
Первый пересчет матрицы — изменяется одно значение, из-за расширения множества разрешенных вершин на вершину «1» мы смогли добраться от вершины «4» до «2», используя более дешевый путь. dkij = min(dk-1ij; dk-1ik + dk-1kj) d142 = min(d042, d041 + d012) d142 = min(4, -1) Вторая итерация, улучшили значение для p43
Результат
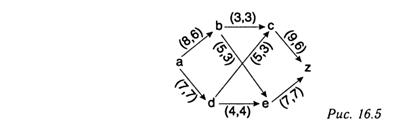
49. Определение сети. Понятие функции потока.
49. Определение сети. Понятие функции потока.
|
|||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 173; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.182.45 (0.016 с.) |
 , a ровно | V | раз. Если при исполнении последней итерации длина кратчайшего пути до какой-либо вершины строго уменьшилась, то в графе есть отрицательный цикл, достижимый из s. На основе этого можно предложить следующую оптимизацию: отслеживать изменения в графе и, как только они закончатся, сделать выход из цикла (дальнейшие итерации будут бессмысленны).
, a ровно | V | раз. Если при исполнении последней итерации длина кратчайшего пути до какой-либо вершины строго уменьшилась, то в графе есть отрицательный цикл, достижимый из s. На основе этого можно предложить следующую оптимизацию: отслеживать изменения в графе и, как только они закончатся, сделать выход из цикла (дальнейшие итерации будут бессмысленны).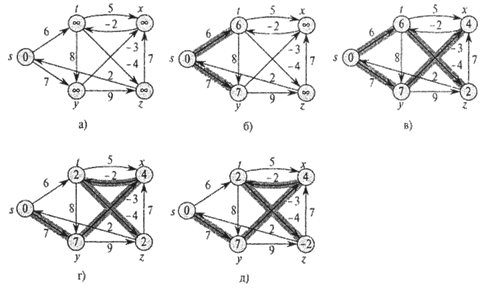
 без петель и дуг отрицательного веса[2]. Найти кратчайшие пути от некоторой вершины
без петель и дуг отрицательного веса[2]. Найти кратчайшие пути от некоторой вершины  графа
графа  до всех остальных вершин этого графа.
до всех остальных вершин этого графа.





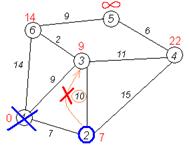
 , устанавливаем метку вершины 4 равной 22.
, устанавливаем метку вершины 4 равной 22.