
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление суммы членов знакочередующегося ряда с заданной точностью и оценка остатка ряда
Согласно признаку Лейбница, знакочередующийся ряд u1 –u2 + u3 - … + (-1)n-1 · un + … сходится, если члены его монотонно убывают по абсолютной величине и Сумма этого ряда по абсолютной величине не превосходит абсолютной величины первого члена ряда, т. е. 0 < |S| <|u1|, а остаток rn по абсолютной величине не превосходит абсолютной величины первого отброшенного члена ряда un+1, т. е. |rn| < |un+1|/ Сумму членов сходящегося ряда можно записать в виде S = Sn + rn, где Sn – частичная сумма ряда. Остаток rn знакочередующегося сходящегося ряда также является знакочередующимся рядом. Если первый член остатка отрицателен, то и остаток отрицателен; тогда Sn > S, т.е. частичная сумма ряда вычисляется с избытком. Если же первый член остатка положителен, то Sn < S, т.е. частичная сумма ряда вычисляется с недостатком. Признак Лейбница позволяет оценить погрешность при приближенных вычислениях с помощью знакочередующихся рядов. Погрешность, допускаемая при замене суммы сходящегося ряда суммой нескольких первых его членов, меньше абсолютной величины первого из отброшенных членов.
Пример 15 Используя признак Лейбница, установить сходимость ряда
Решение:
знакочередующийся. Согласно признаку Лейбница, он сходится. Имеем S = S4 + r4, или S = 1 - S4 = 1 - Так как |r4| < |u5|, то |r4| < Сумма ряда S Степенные ряды Степенным рядом называется ряд вида
где числа a0, a1, a2, …, an,… называются коэффициентами ряда, а член anxn – общим членом ряда. Областью сходимости степенного ряда называется множество всех значений х, при которых данный ряд сходится. Число R называется радиусом сходимости ряда (3), если при |х| < R ряд сходится и притом абсолютно, а при |x| > R ряд расходится. Радиус сходимости R можно найти, используя признак Даламбера:
(х не зависит от n), откуда |x| < т.е. ряд (3) сходится при любых х, удовлетворяющих условию (4), и расходится при |x| > Отсюда следует, что если существует предел R = То радиус сходимости ряда R равен этому пределу и ряд (3) сходится при |х| < R, т. е. в промежутке - R < x < R, который называется промежутком (интервалом) сходимости.
Если предел (6) равен нулю (R = 0), то ряд (3) сходится в единственной точке х = 0. На концах промежутка ряд может сходиться (абсолютно или условно), но может и расходиться. Стоимость ряда (3) при х = - R и при х = R исследуется с помощью какого – либо из признаков сходимости.
Пример 16 Дан ряд Исследовать его сходимость в точках х = 1, х = 3, х = -2
Решение: При х = 1 данный ряд превращается в числовой ряд
Исследуем сходимость этого ряда по признаку Даламбера. Имеем:
При х = 3 получим ряд
который расходится, так как не выполняется необходимый признак сходимости ряда (
При х = - 2 получим
Это знакочередующийся ряд, который, согласно признаку Лейбница, сходится. Итак, в точках х = 1 и х = -2 ряд сходится, а в точке х = 3 расходится.
Пример 17 Найти промежуток сходимости степенного ряда:
Решение: Используя формулу (6) получим an =
R = Следовательно, промежуток сходимости есть -
Вопросы для самопроверки: 1. Какая сумма называется числовым рядом? 2. Какие числа называются членами ряда? 3. Что такое общий член ряда? 4. Какие суммы называются частичными суммами ряда? 5. Какой ряд называется сходящимся? 6. Какой ряд называется расходящимся? 7. Какая разность называется остатком ряда? 8. Какой ряд называется геометрическим рядом? 9. Какой ряд называется гармоническим? 10. Сформулировать необходимый признак сходимости ряда? 11. Сформулировать признак сравнения рядов с положительными членами? 12. Сформулировать признак Даламбера. 13. Какой числовой ряд называется знакопеременным? 14. Сформулировать признак сходимости Лейбница для знакочередующихся рядов. 15. Какой знакопеременный ряд называется абсолютно сходящимся? 16. Какой знакопеременный ряд называется условно сходящимся? 17. Какой ряд называется степенным рядом? 18. Что называется областью сходимости степенного ряда? 19. Что называется радиусом сходимости степенного ряда?
20. Что называется промежутком сходимости? 21. Какой ряд называется рядом Тейлора? 22. Какой ряд называется рядом Маклорена?
|
||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 4543; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.147.53 (0.009 с.) |
 =0.
=0. и оценить погрешность, допускаемую при замене суммы членов этого ряда суммой первых четырех его членов
и оценить погрешность, допускаемую при замене суммы членов этого ряда суммой первых четырех его членов
 , откуда
, откуда ; S = 0,7986 + r4
; S = 0,7986 + r4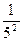 = 0, 04 (r4 > 0); следовательно, 0 < r4 < 0,04.
= 0, 04 (r4 > 0); следовательно, 0 < r4 < 0,04.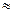 0,7986 (с недостатком) вычислена с погрешностью, не превышающей 0,04.
0,7986 (с недостатком) вычислена с погрешностью, не превышающей 0,04. (3)
(3) |x|
|x|  < 1
< 1 (4)
(4) 0, n = 1, 2, 3, …) (6)
0, n = 1, 2, 3, …) (6)

 ;
;  ;
; 
 < 1, т. е. ряд сходится.
< 1, т. е. ряд сходится. или 1 + 2+ 3 + … + n + …,
или 1 + 2+ 3 + … + n + …, ).
). или
или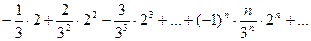

 ; an+1 =
; an+1 = 

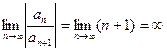
 , т.е. данный ряд сходится на всей числовой оси
, т.е. данный ряд сходится на всей числовой оси


