
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о дифференциальном уравнении.
Дифференциальным уравнением называется уравнение, связывающее независимую переменную, искомую функцию, ее производную (или дифференциал аргумента и дифференциал функции). Если дифференциальное уравнение содержит производную или дифференциал не выше первого порядка, то оно называется дифференциальным уравнением первого порядка. Общий вид такого уравнения F(x, у, у') =0, где y=f(x)-искомая неизвестная функция у' = f'(х) - ее производная по х, a F-заданная функция переменных х, у, у'. Общим решением дифференциального уравнения первого порядка называется функция у = j(х, с) от х и произвольной постоянной С, обращающая это уравнение в тождество по х. Общее решение, записанное в неявном виде Ф(х, у, С) =0, называется общим интегралом. Частным решением уравнения F(x, у, у')=0 называется решение, полученное из общего решения при фиксированном значении С: y=j(x, С0), где С0 — фиксированное число. Частным интегралом уравнения F(x, у, у')=0 называется интеграл, полученный из общего интеграла при фиксированном значении С: Ф(х, у, С0) =0. График любого частного решения дифференциального уравнения F(x, у, у')=0 называется интегральной кривой. Общему решению (и общему интегралу) этого уравнения соответствует семейство интегральных кривых, зависящих от одного параметра. Задача нахождения частного интеграла дифференциального уравнения n-го порядка (n=1, 2, 3,...), удовлетворяющего начальным условиям вида у(х0) = у0, у'(х0) = y'0, y"(х0)=y"0…y(n-1)(х0) =yо(n-1)0 называется задачей Коши. Задача Коши для дифференциального уравнения первого порядка состоит в том, чтобы найти решение, удовлетворяющее начальному условию у(х0) = у0. Другими словами, из всех интегральных кривых данного дифференциального уравнения требуется выделить ту, которая проходит через данную точку (x0, y0).
Пример 2. Составить уравнение кривой y = f(x), если угловой коэффициент касательной, проведенной в любой точке кривой, равен 2х. Решение. Так как на основании геометрического смысла производной y'=kкас, то получим дифференциальное уравнение первого порядка:
Чтобы найти искомую функцию y=f(x), надо проинтегрировать обе части уравнения òdy = ò2xdx. Отсюда получим общее решение дифференциального уравнения:
у = х2 + С. Геометрически это решение представляет собой семейство парабол с вершиной на оси Оу, симметричных относительно этой оси (рис. 68).
Чтобы из общего решения выделить частное решение, надо задать начальные условия. Пусть у = - 1 при х = 1; тогда общее решение примет вид -1 = 1 + С, откуда С = - 2. Геометрически частное решение у = х2 - 2 представляет собой параболу, проходящую через точку (1,-1) (рис. 68).
Дифференциальные уравнения с разделяющимися переменными.
Общий вид такого уравнения X(х)Y(у)dx + Х1(х)У1(у)dy=0, где Х(х), X1(x) - функции только от х, Y(y), Y1 (y) - функции только от у. Поделив обе части уравнения на произведение Х1 (х) Y(y)≠0, получим уравнение с разделенными переменными:
Общий интеграл этого уравнения имеет вид
Замечание. Если произведение X1(x)Y(y)=0 при х = а и у = b, то эти функции х=а и у=b являются решениями дифференциального уравнения при условии, что при этих значениях х и у уравнение не теряет числового смысла. Геометрически эти решения представляют собой прямые, параллельные осям координат.
Пример 3. Решить уравнение у dy = x dx. Найти частное решение, удовлетворяющее условию у = 4 при х = - 2. Решение. Это уравнение с разделенными переменными. Интегрируя, находим общее решение уравнения:
Для получения более простого по форме общего решения постоянное слагаемое в правой части представлено в виде С/2. Тогда у2 = х2 + С Подставив в общее решение значения у = 4 и х = - 2, получим 16 = 4 + С, откуда С = 12. Итак, частное решение уравнения, удовлетворяющее данному условию, имеет вид у2 = х2 + 12.
Пример 4. Решить уравнение (1+ех)уу' = ех. Найти частное решение, удовлетворяющее условию у= 1 при х = 0. Решение. Так как
Разделим обе части уравнения на 1 + ех:
Интегрируя, находим
или
После потенцирования получим решение
При у = 1 и х = 0 имеем е1/2 = С(1 + е0), Итак, частный интеграл уравнения, удовлетворяющий данному условию, имеет вид
Линейные дифференциальные уравнения первого порядка.
Общий вид такого уравнения у' =f(x)y+q(x) (1) где f(x) и q(x) - заданные функции от х. Это уравнение является линейным относительно искомой функции и ее производной.
Если q(x)=0, то линейное дифференциальное уравнение (1) называется однородным. Оно имеет вид у' =f(x)y и решается методом разделения переменных:
где F(х)-некоторая первообразная функции f(x), a C = ±C1 - произвольная постоянная. Если f(x)=0, то уравнение (1) принимает вид у' = q(x) и решается методом разделения переменных:
где Q(x) - некоторая первообразная функции q(x), a С - произвольная постоянная. Существуют различные приемы решения линейного неоднородного дифференциального уравнения. Рассмотрим два из них. 1. Этот прием решения основан на применении следующей теоремы: если у=j(х) - некоторое решение уравнения (1), то все решения этого уравнения задаются формулой
еде
Пример 5. Найти общее решение дифференциального уравнения у' – у ctg х = sin x. Решение. Данное уравнение является линейным. Полагаем y=uv, тогда у'=u'v+v'u и уравнение преобразуется к виду u'v+v'u-uv ctg х = sin x, или u'v+u(v'-v ctg x) = sin x. Так как один множитель можно выбрать произвольно, то выберем в качестве v какой-либо частный интеграл уравнения v'-v ctg x=0. Тогда для отыскания u получим уравнение u'v = sin х. Решим уравнение v'-v ctg x=0; имеем
В качестве v выбран частный интеграл уравнения при С = 0. Подставляя значение v во второе уравнение и решая его, найдем u, как общий интеграл этого уравнения: u' sin х = sin x, u' = 1, du = dx, u = x + С. Зная u и v, находим искомую функцию у: у = (x + С) sin x.
Пример 6. Найти частное решение дифференциального уравнения у'+2ху=2х2 Решение. Положим y = uv; тогда y' = u'v+v'u и данное уравнение примет вид u'v + uv' + 2xuv = 2х2 или u'v + u (v' + 2xv) = 2х2 Положим v'+2ху = 0; тогда
Проинтегрировав, получим частное решение ln v =-х2, или v = - u' du = 2x2dx, откуда Общее решение данного дифференциального уравнения:
Подставив в это равенство начальные условия, получим 0 = е0(0+С), откуда С = 0. Итак, частное решение данного дифференциального уравнения, удовлетворяющее данному условию, имеет вид
|
||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 636; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.28.50 (0.016 с.) |
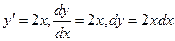




 , то
, то , откуда (1+ех)уdy = ехdx
, откуда (1+ех)уdy = ехdx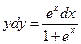



 = 2С, откуда С =
= 2С, откуда С = 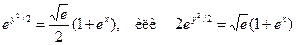





 - общее решение однородного уравнения. Иными словами, для нахождения общего решения уравнения (1) достаточно найти хотя бы одно его частное решение.
- общее решение однородного уравнения. Иными словами, для нахождения общего решения уравнения (1) достаточно найти хотя бы одно его частное решение.

 , удовлетворяющее условию у=0 при x=0.
, удовлетворяющее условию у=0 при x=0. 







