
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1.3 Дифференциальные уравнения в частных производных
Дифференциальные уравнения в частных производных.* Л4, глава 15, стр 243 – 256
Тема 1.4 Ряды Числовые ряды. Сходимость и расходимость числовых рядов. Признак сходимости Даламбера. Знакопеременные ряды.* Абсолютная и условная сходимость рядов.* Функциональные ряды*. Степенные ряды*. Разложение элементарных функций в ряд Маклорена*. Практическое занятие № 10 «Числовые ряды. Необходимый признак сходимости. Признак Даламбера.» Практическое занятие № 11 «Знакопеременные и знакочередующиеся ряды. Абсолютная и условная сходимость.»* Практическое занятие № 12 «Нахождение радиуса и промежутка сходимости степенного ряда»* Практическое занятие № 13 «Разложение функций в ряд Маклорена.»*
Л4, глава 27, стр. 391 – 417
Методические указания Числовые ряды. Необходимый признак сходимости ряда. Достаточные признаки сходимости рядов с положительными членами Основные понятия. Числовым рядом называется сумма вида
где числа u1, u2, u3, … un, … называемые членами ряда, образуют бесконечную последовательность; член un называется общим членом ряда. Суммы S1 = u1, S2 = u1 + u2, S3 = u1 + u2 + u3, …………… Sn = u1 + u2 + u3 + … + un составленные из первых членов ряда (1), называются частичными суммами этого ряда. Каждому ряду можно сопоставить последовательность частичных сумм S1, S2, S3, …, Sn, …Если при бесконечном возрастании номера n частичная сумма ряда Sn стремится к пределу S, то ряд называется сходящимся, а число S – суммой сходящегося ряда, т.е.
Эта запись равносильна записи
Если частичная сумма Sn ряда (1) при неограниченном возрастании n не имеет конечного предела (в частности, стремится к + Если ряд сходится, то значение Sn при достаточно большом n является приближенным выражением суммы ряда S. Разность rn = S - Sn называется остатком ряда. Если ряд сходится, то его остаток стремится к нулю, т.е.
Геометрический ряд. Рассмотрим несколько случаев нахождения частичной суммы первых n членов ряда 1. |q| < 1. Для нахождения частичной суммы Sn воспользуемся формулой суммы членов убывающей геометрической прогрессии:
где a1 – первый член, an = a1qn-1 - n-й член, q – знаменатель прогрессии. Следовательно
Находим сумму ряда
Поскольку первое слагаемое под знаком предела является постоянным, а второе – бесконечно малой величиной ( данном случае ряд сходится, а его сумма есть
2. |q| > 1. Частичную сумму Sn найдем по формуле суммы членов возрастающей геометрической прогрессии:
Тогда сумма ряда
так как первое слагаемое под знаком предела есть бесконечно большая величина (
3. q = 1. Находим Sn = а1 + а1 + а1 + … + а1 = а1n Следовательно, расходится.
4. q = -1. Имеем S1 = a S2 = a – a = 0 S3 = a – a + a = f S4 = a – a + a – a = 0 ……………………. т.е. Sn = 0 при n четном и Sn = а при n нечетном.. Отсюда следует, что последовательность частичных сумм не имеет предела и, значит, ряд расходится. Итак, данный ряд сходится при |q |< 1 и расходится при |q| ≥ 1. Ряд вида
Гармонический ряд. Ряд вида
называется гармоническим. Запишем частичную сумму этого ряда Sn = (1 + Сумма Sn больше суммы, представленной следующим образом: Sn > (1 + или Sn > 1 + Если 1 + Следовательно, если
Необходимый признак сходимости ряда . Ряд Если
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 180; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.63.145 (0.01 с.) |
 (1)
(1)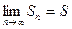 или
или 

 или к -
или к - 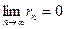 , и наоборот если остаток стремится к нулю, то ряд сходится.
, и наоборот если остаток стремится к нулю, то ряд сходится.
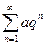 , образованного из членов геометрической прогрессии.
, образованного из членов геометрической прогрессии.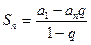 .
.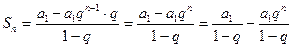

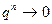 при
при  ). Таким образом, в
). Таким образом, в
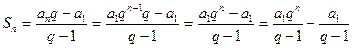

 при
при  . Значит, в данном случае ряд
. Значит, в данном случае ряд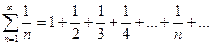



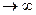 , или Sn = 1 +
, или Sn = 1 + 
 может сходиться только при условии, что его общий член un при неограниченном увеличении номера n стремиться к нулю:
может сходиться только при условии, что его общий член un при неограниченном увеличении номера n стремиться к нулю:  .
. , то ряд
, то ряд 


