
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства смешанного произведения.
10 Смешанное произведение векторов Здесь знак “+” берется в случае, если тройка векторов - правая, “-” если она левая. 20 Векторы 30 При перестановке местами любых двух векторов смешанного произведения оно меняет свой знак на противоположный; т.е. 4. Постоянный сомножитель можно выносить из любого сомножителя смешанного произведения, т.е. для любых векторов 5. Смешанное произведение дистрибутивно для любого сомножителя, т.е. для любых векторов Теорема. Пусть в базисе
Осн. лит.: 1, [34-48], 19, [12-20, 66-72, 83-87] Доп. лит.: 30, [41-109]. Контрольные вопросы 1.В чем отличие скалярного произведения от векторного произведения векторов? Перечислите основные свойства скалярного и векторного произведений. 2. Что называется смешанным произведением? 3. Укажите условие коллинеарности двух векторов. Лекция № 4. Аналитическая геометрия. Плоскость Пусть плоскость Это уравнение называется уравнением плоскости, проходящей через три заданные точки. Теорема. Любая плоскость Определение. Вектор Теорема о нормальном векторе плоскости. Вектор Следствие 1. Косинус угла
с нормальными векторами
Следствие 2. Эти плоскости перпендикулярны только в том случае, когда
Следствие 3. Эти плоскости параллельны только в том случае, когда
Если же Пусть плоскость
Это уравнение называется уравнением плоскости с нормальным вектором. Пусть плоскость Это уравнение называется уравнением плоскости в отрезках Теорема. Расстояние от точки
Осн. лит.: 1, [49-71], 9, [23-33] Доп. лит.: 29, [199-206] Контрольные вопросы 1. Условие параллельности плоскостей. 2. Условие перпендикулярности плоскостей. 3. Расстояние от точки до плоскости
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 197; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.211.107 (0.007 с.) |
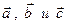 равно
равно 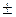 объему параллелепипеда, построенного на этих векторах:
объему параллелепипеда, построенного на этих векторах: 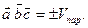
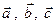 - являются компланарными только в том случае, когда их смешанное произведение равно 0:
- являются компланарными только в том случае, когда их смешанное произведение равно 0: 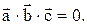
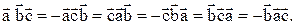
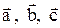 и числа
и числа 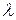
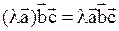 .
.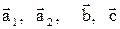 верно:
верно: 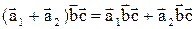 .
.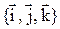 векторы
векторы 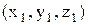 ,
, 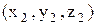 и
и 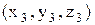 , тогда их смешанное произведение записывается в виде определителя:
, тогда их смешанное произведение записывается в виде определителя: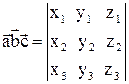 .
. проходит через три точки
проходит через три точки  ,
,  и
и  , не лежащие на одной прямой. Тогда векторы
, не лежащие на одной прямой. Тогда векторы 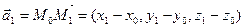 и
и 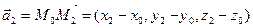 являются направляющими для плоскости
являются направляющими для плоскости  , подставив их координаты в уравнение с направляющими векторами, получим:
, подставив их координаты в уравнение с направляющими векторами, получим:  .
. в пространстве
в пространстве  определяется своим общим уравнением вида
определяется своим общим уравнением вида  , где
, где  , задает некоторую плоскость в пространстве.
, задает некоторую плоскость в пространстве. , перпендикулярный плоскости
, перпендикулярный плоскости  с координатами
с координатами  является нормальным для плоскости
является нормальным для плоскости  в пространстве
в пространстве  между плоскостями
между плоскостями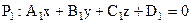 и
и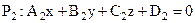
 и
и  находится по формуле:
находится по формуле: .
. .
. .
. , то плоскости
, то плоскости 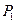 и
и 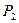 совпадают.
совпадают. перпендикулярно вектору
перпендикулярно вектору 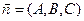 . Возьмем на плоскости произвольную точку M(x,y,z) и составим вектор
. Возьмем на плоскости произвольную точку M(x,y,z) и составим вектор  =
=  . При любом расположении точки М на плоскости вектора
. При любом расположении точки М на плоскости вектора  взаимно перпендикулярны, поэтому их скалярное произведение равно нулю.
взаимно перпендикулярны, поэтому их скалярное произведение равно нулю. 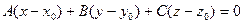 .
. в точках с координатами
в точках с координатами  и
и  соответственно. Тогда уравнение этой плоскости имеет вид:
соответственно. Тогда уравнение этой плоскости имеет вид: 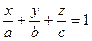 .
. определяется формулой:
определяется формулой: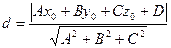 .
.


