
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные дифференциальные уравнения n-го порядка ⇐ ПредыдущаяСтр 8 из 8
Линейные дифференциальные уравнения 2-го порядка содержат все основные, типичные черты уравнений Однородное линейное дифференциальное уравнение
Для него, как и для линейного дифференциального уравнения 2-го порядка, справедливы теоремы о частных решениях 1 и 2. То есть линейные комбинации частных решений также являются решениями и если известно одно или несколько решений, то можно понизить порядок на одну или более единиц. Определение. Фундаментальной системой решений уравнения (1) называется всякая система
В этом случае Из определения ледует, что нулевое решение не входит в фундаментальную систему решений. Например,
что противоречит определению фундаментальной системы решений. Таким образом, фундаментальная система решений не может содержать ни одного Далее, вронскиниан фундаментальной системы решений (и только фундаментальной системы решений) отличен от тождественного нуля. Вронскиниан в общем случае имеет вид:
Формула Остроградского-Лиувилля также имеет место в общем случае:
Из нее также следует, что Существование фундаментальной системы решений доказывается аналогично дифференциальному уравнению 2-го порядка. Основная теорема устанавливает, что общее решение однородного линейного дифференциального уравнения
Неоднородное линейное дифференциальное уравнение
Теоремы о частных решениях справедливы и в эом случае. Также, как и метод Лагранжа вариации произвольных постоянных:
Однородное линейное дифференциальное уравнение
Характеристическое уравнение:
Любому действительному
Так как
Таким образом, в общем случае решение однородного линейного дифференциального уравнения
где И, наконец, 2 теоремы о приведении к дифференциальным уравнениям с постоянными коэффициентами. Теорема 1. Если линейное дифференциальное уравнение
допускает приведение к дифференциальному уравнению с постоянными коэффициентами при помощи замены независимой переменной
Теорема 2. Если (*) допускает приведение к дифференциальному уравнению с постоянными коэффициентами при помощи подстановки
Для неоднородных линейных дифференциальных уравнений приведение осуществляется по тем же формулам.
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 115; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.115.179 (0.006 с.) |
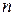 -го порядка.
-го порядка. . (1)
. (1) , которая обладает следующим свойством: ни при каких
, которая обладает следующим свойством: ни при каких  ,
,  , одновременно не равных нулю, линейная комбинация
, одновременно не равных нулю, линейная комбинация . (а)
. (а) , удовлетворяющие (а), называют линейно независимыми.
, удовлетворяющие (а), называют линейно независимыми.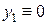 ,
,  . Тогда, положив
. Тогда, положив  , …,
, …,  , получим
, получим ,
, . При
. При  новое определение тождественно старому.
новое определение тождественно старому. .
. .
. либо тождественно равен нулю, либо не равен нулю ни при каком
либо тождественно равен нулю, либо не равен нулю ни при каком  . Первый случай соответствует не фундаментальной системе решений, второй – фундаментальной системе решений.
. Первый случай соответствует не фундаментальной системе решений, второй – фундаментальной системе решений. , где
, где  .
. .
.
 ,
, , действительные числа.
, действительные числа. .
. -кратному корню
-кратному корню  соответствуют решения:
соответствуют решения: ,
, 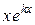 ,
,  .
. – действительные числа, то комплексные корни характеристического уравнения встречаются только сопряженными парами и имеют одинаковую кратность. Любой паре
– действительные числа, то комплексные корни характеристического уравнения встречаются только сопряженными парами и имеют одинаковую кратность. Любой паре  кратности
кратности  частных решений:
частных решений: ,
, 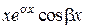 , …,
, …,  ,
, ,
,  , …,
, …,  .
. ,
, и
и 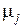 – кратности корней, а
– кратности корней, а  ,
,  ,
,  – многочлены соответствующих степеней.
– многочлены соответствующих степеней. , то такой цели служит только подстановка
, то такой цели служит только подстановка , где
, где  .
. , преобразующей неизвестную функцию
, преобразующей неизвестную функцию  , то такое преобразование выполняется только, если положить
, то такое преобразование выполняется только, если положить



