
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Простейшие дифференциальные уравнения иСтр 1 из 8Следующая ⇒
Простейшие дифференциальные уравнения и Методы их интегрирования.
Опр. Дифференциальными уравнениями называются уравнения, содержащие неизвестные функции, их аргументы и производные от неизвестных функций по этим аргументам, или дифференциалы неизвестных функций. Д.у. называется обыкновенным, если неизвестные функции зависят только от одной переменной. (1) F(x,y,y’, …, y(n)) = 0: (2) Ф(x,y,dy, …,, d(n) y) = 0. Примеры.
Основные понятия теории дифференциальных уравнений.
Порядок старшей входящей в уравнение производной определяет порядок уравнения - n. Любая функция, которая при подстановке в уравнение вместо неизвестной обращает его в тождество, называется решение этого уравнения. Например, sin(x) есть решение уравнения второго порядка Совокупность всех частных решений называют общим решением. Отметим, что общее решение д.у. n-го порядка содержит n произвольных констант, т.е. имеет вид:
Для уравнения n-го порядка начальные условия чаще всего задаются следующим образом: требуется найти решение д.у., которое при заданном значении
Задача о решении д.у., удовлетворяющем начальным условия вида (*) называется задачей Коши. Для уравнения 1-го порядка задача Коши сводится к поиску решения, которое при
Интегрирование простейших типов д.у. 1-го порядка.
Существование ФСР (2)
Теорема: Любое однородное линейное дифференциальное уравнение имеет фундаментальную систему решений. Доказательство: Рассмотрим дифференциальное уравнение
и две системы начальных условий:
где
Пусть
Теорема доказана.
Основная теорема: Общее решение линейного однородного дифференциального уравнения 2-го порядка является линейной комбинацией с произвольными постоянными коэффициентами любых двух решений этого уравнения, образующих фундаментальную систему решений. Другими словами, общее решение линейного однородного дифференциального уравнения 2-го порядка есть сумма двух частных решений линейно независимых решений, умноженных на произвольные постоянные. Доказательство: Пусть
где Пусть
Положим
отсюда
Так как Теоремы о частных решениях
Рассмотрим неоднородное уравнение
и соответствующее однородное уравнение
Теорема 1: Разность любых двух частных решений уравнения (1) есть частное решение соответствующего однородного дифференциального уравнения. Доказательство: Пусть
Теорема доказана.
Теорема 2: Если
есть новое частное решение уравнения (1). Доказательство: Справедливы следующие соотношения:
значит,
Теорема доказана.
Из теорем 1 и 2 следует, что, взяв любое одно частное решение неоднородного уравнения (1) и прибавляя всевозможные частные решения однородного уравнения (2), получим все без исключения частные решения уравнения (1). Определение: Общее решение
где
Теорема 3: Если правая часть уравнения (1) есть сумма двух функций Доказательство: Рассмотрим уравнение
Теорема доказана.
Пример:
Тогда Случай 1.
Этот случай соответствует
где 1) многочлен 2) многочлен 3) многочлен В первом случае
из которого можно найти неопределеные коэффициенты Во втором случае,
В третьем случае
Правило 1. Если
где Пример.
Случай 2.
Сделаем замену
Таким образом, уравнение (*) сведено к частному случаю, рассмотренному выше. Следовательно:
1. Если 2. 3. Правило 2. Если
где Пример.
Перейдем теперь к общему случаю:
Вспомогательная теорема. Пусть в уравнении
Положим
отсюда, по равенству комплексных чисел, следует доказательство теоремы. Следствие. Если
Заменим теперь в общем уравнении
перегруппируем и введем новые обозначения:
тогда
Замечание. При использовании (**) надо помнить, что вид Пример.
9.4.3. Линейные дифференциальные уравнения, приводящиеся к уравнениям с постоянными коэффициентами
Теорема. Линейное дифференциальное уравнение преобразуется снова в линейное дифференциальное уравнение при всяком линейном преобразовании неизвестной функции и любом преобразовании аргумента (и только при таких преобразованиях). Доказательство.
В уравнении
положим
и исходное уравнение преобразуется к виду
и это уравнение снова является линейным, так как все коэффициенты и правая часть есть функции только Положим, что
Подставляя эти значения, получим опять линейное уравнение:
заменяя Предположим теперь, что
Подставляя
Чтобы (*) было линейным, нужно, чтобы
и тогда
есть функция от
Очевидно, что для преобразования линейного дифференциального уравнения с переменными коэффициентами в линйое дифференциальное уравнение с постоянными коэффициентами достаточно рассмотреть соответствующее однородное уравнение. Согласно теореме, сохранение линейности возможно только в двух случаях: при линейном преобразовании функции Теперь выведем условия, налагаемые на Необходимое и достаточное условие для преобразования Итак, пусть дано уравнение
и подстановка
подставляя в уравнение, получим:
и потребуем, чтобы коэффициенты при
Тогда
Последнее равенство можно записать, как
(3) и есть условие приводимости (1) к (2), в котором коэффициенты являются постоянными. Найдем теперь
Положим
Таким образом, преобразование выполняется, если выполнено (3). Пример.
Условие (3) выполняется и
Необходимое и достаточное условие для преобразования Пусть
Далее,
Из (*), считая
Кроме того,
( Найдем теперь
где Таким образом, если выполняется ( Пример. Рассмотрим уравнение Эйлера
здесь Теорема 1. Если линейное дифференциальное уравнение
допускает приведение к дифференциальному уравнению с постоянными коэффициентами при помощи замены независимой переменной
Теорема 2. Если (*) допускает приведение к дифференциальному уравнению с постоянными коэффициентами при помощи подстановки
Для неоднородных линейных дифференциальных уравнений приведение осуществляется по тем же формулам.
Теорема Коши. Если
Произвольно изменяя
– такое решение называется общим. Частное решение всегда можно получить из общего. Системы дифференциальных уравнений типа (1) и дифференциальные уравнения Нормальная система линейных дифференциальных уравнений с постоянными коэффициентами имеет вид:
Рассмотрим метод интегрирования системы (2) приведением е к одному линейному дифференциальному уравнению
Затем продифференцируем и его по
Выражая из первых
– линейное дифференциальное уравнение Найдя общее решение (**) Пример.
Получим систему
Дифференцируя
Простейшие дифференциальные уравнения и Методы их интегрирования.
Опр. Дифференциальными уравнениями называются уравнения, содержащие неизвестные функции, их аргументы и производные от неизвестных функций по этим аргументам, или дифференциалы неизвестных функций. Д.у. называется обыкновенным, если неизвестные функции зависят только от одной переменной. (1) F(x,y,y’, …, y(n)) = 0: (2) Ф(x,y,dy, …,, d(n) y) = 0. Примеры.
Основные понятия теории дифференциальных уравнений.
Порядок старшей входящей в уравнение производной определяет порядок уравнения - n. Любая функция, которая при подстановке в уравнение вместо неизвестной обращает его в тождество, называется решение этого уравнения. Например, sin(x) есть решение уравнения второго порядка Совокупность всех частных решений называют общим решением. Отметим, что общее решение д.у. n-го порядка содержит n произвольных констант, т.е. имеет вид:
Для уравнения n-го порядка начальные условия чаще всего задаются следующим образом: требуется найти решение д.у., которое при заданном значении
Задача о решении д.у., удовлетворяющем начальным условия вида (*) называется задачей Коши. Для уравнения 1-го порядка задача Коши сводится к поиску решения, которое при
|
|||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 144; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.142.128 (0.189 с.) |
 . Дифференциальные уравнения имеют бесконечное множество решений, если имеется хотя бы одно. Обычно, при решении ставиться задача нахождения всех его решений. Процесс решения д.у. часто называют интегрирование д.у.. Если же решается конкретная задача (в физике, технике и т.д.) по нахождению решения д.у., то на неизвестную функцию налагаются как правило дополнительные условия. Например, функция должна принимать определенные значения при заданных значениях аргумента. Такие условия называют начальными условиями, а конкретное решение – частным решением д.у..
. Дифференциальные уравнения имеют бесконечное множество решений, если имеется хотя бы одно. Обычно, при решении ставиться задача нахождения всех его решений. Процесс решения д.у. часто называют интегрирование д.у.. Если же решается конкретная задача (в физике, технике и т.д.) по нахождению решения д.у., то на неизвестную функцию налагаются как правило дополнительные условия. Например, функция должна принимать определенные значения при заданных значениях аргумента. Такие условия называют начальными условиями, а конкретное решение – частным решением д.у..
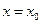 принимает вместе со своими производными вплоть до (n-1) порядка, наперед заданные значения:
принимает вместе со своими производными вплоть до (n-1) порядка, наперед заданные значения: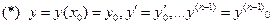 при
при  .
.
 ,
,  ,
,  ,
, ,
,  ,
, .
.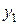 и
и 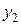 – частные решения соответствующих задач Коши. Докажем, что они образуют фундаментальную систему:
– частные решения соответствующих задач Коши. Докажем, что они образуют фундаментальную систему: .
. – фундаментальная система решений. Составим линейную комбинацию
– фундаментальная система решений. Составим линейную комбинацию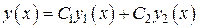 ,
,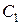 ,
, 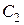 есть произвольные постоянные. Надо доказать, что любое частное решение можно получить из
есть произвольные постоянные. Надо доказать, что любое частное решение можно получить из  выбором
выбором 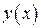 есть решение задачи Коши для начальных условий
есть решение задачи Коши для начальных условий ,
,  .
. ,
,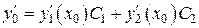 ,
, и
и  .
. , то
, то  (1)
(1) вместе с ее производными:
вместе с ее производными: .
. – частное решение уравнения (1),
– частное решение уравнения (1),  – частное решение соответствующего однородного уравнения, то
– частное решение соответствующего однородного уравнения, то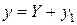
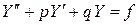 ,
,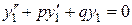 ,
, .
. ,
, и
и  , и если
, и если  есть частное решение уравнения (1) с правой частью
есть частное решение уравнения (1) с правой частью  – частное решение уравнения (1) с правой частью
– частное решение уравнения (1) с правой частью  – частное решение уравнения (1) с правой частью
– частное решение уравнения (1) с правой частью 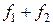 .
. , подставим
, подставим  и
и  соответственно. После сложения последних уравнений и группировки слагаемых получим:
соответственно. После сложения последних уравнений и группировки слагаемых получим: .
.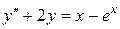 , (1)
, (1) ,
,  , (2)
, (2) ,
,  . (3)
. (3) – частное решение уравнения (1).
– частное решение уравнения (1). ,
, 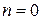 ,
, 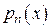 –
– 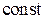 .
.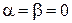 .
.  . Подставим
. Подставим  в (8), получим
в (8), получим ,
,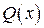 есть:
есть: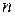 -ной степени, если
-ной степени, если 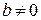 .
. -й степени, если
-й степени, если  ,
, 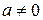 .
. -й степени, если
-й степени, если 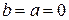 .
.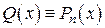 , (*)
, (*) есть корень характеристического уравнения, тождество (*) невозможно, так как степень
есть корень характеристического уравнения, тождество (*) невозможно, так как степень  . При этом степень
. При этом степень  .
. , то есть
, то есть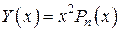 .
.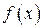 есть
есть  надо искать в виде
надо искать в виде ,
, – многочлен
– многочлен  – кратность корня
– кратность корня 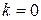 . Для вычисления неопределенных коэффициентов
. Для вычисления неопределенных коэффициентов  ,
,  , корень
, корень  ,
,

 ,
,  ,
,  и
и .
.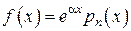 ,
, 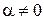 ,
, . (*)
. (*)
 ,
, 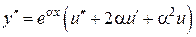
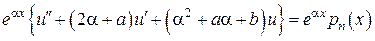
 , где
, где ,
,  .
. , тогда
, тогда 
 , где коэффициенты
, где коэффициенты  ,
,  , то есть если
, то есть если 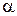 – простой корень характеристического уравнения, то
– простой корень характеристического уравнения, то 
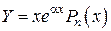 .
.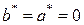 , то есть
, то есть 
 .
. ,
, ,
,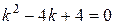

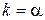 и
и  .
.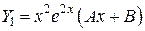 , подставляя в дифференциальное уравнение, получим:
, подставляя в дифференциальное уравнение, получим: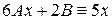
 ,
,  ,
, 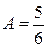 .
. .
. .
. (*)
(*) есть решение уравнения
есть решение уравнения  ,
,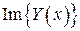 есть решение уравнения
есть решение уравнения 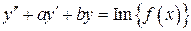 .
.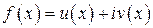 ,
, 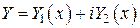 . Дважды дифференцируя
. Дважды дифференцируя 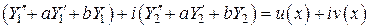 ,
, есть решение уравнения
есть решение уравнения  , то
, то  есть решение уравнения
есть решение уравнения  .
. и
и 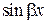 по формулам Эйлера:
по формулам Эйлера: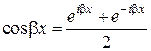 ,
,  ,
, ,
, 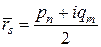 ,
,  ,
, .
. , то в (**) мы должны брать
, то в (**) мы должны брать  , если
, если  , то в (**) следует взять
, то в (**) следует взять  , и если
, и если  , то в (**) возьмем
, то в (**) возьмем  , и т. д.
, и т. д. ,
, ,
, 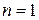 ,
,  ,
,  ,
, , так как
, так как  не корень характеристического уравнения,
не корень характеристического уравнения, ,
, ,
,  ,
,  ,
,  , и т. д.
, и т. д. , где
, где 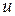 и
и  – известные функции. Тогда
– известные функции. Тогда ,
, ,
,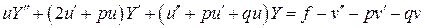 ,
, , тогда
, тогда  и
и ,
, 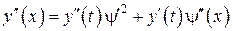 .
. ,
, найдем, что все коэффициенты и правая часть есть функции только
найдем, что все коэффициенты и правая часть есть функции только  . На этом доказательство первой части закончено.
. На этом доказательство первой части закончено. . Тогда
. Тогда ,
, 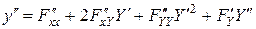 .
. и
и  в исходное уравнение, получим в общем случае нелинейное уравнение
в исходное уравнение, получим в общем случае нелинейное уравнение . (*)
. (*) и
и  не зависели от
не зависели от  , а
, а  содержало
содержало  в линейную функцию. Если
в линейную функцию. Если
 ,
, не зависит от
не зависит от 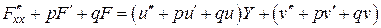
 (
( , так как она не входит в коэффициенты в левой части) и при произвольном преобразовании
, так как она не входит в коэффициенты в левой части) и при произвольном преобразовании  и
и  линейного дифференциального уравнения 2-го порядка, при которых это уравнение может быть приведено к линейному дифференциальному уравнению 2-го порядка с постоянными коэффициентами с помощью преобразования
линейного дифференциального уравнения 2-го порядка, при которых это уравнение может быть приведено к линейному дифференциальному уравнению 2-го порядка с постоянными коэффициентами с помощью преобразования 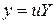 или
или  ,
, ,
, , (2)
, (2) были константами:
были константами: .
. . Отсюда
. Отсюда  или
или
 или
или .
. , где
, где  . (3)
. (3) , с помощью которой это приведение выполняется:
, с помощью которой это приведение выполняется:

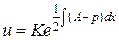 .
. и
и  , тогда
, тогда 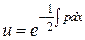 и
и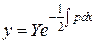 .
. .
. приводит к уравнению
приводит к уравнению .
. и
и 
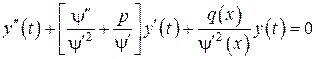 . (
. ( )
)

 , имеем
, имеем 
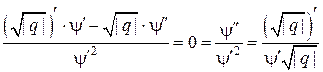 .
. . Подставляя эти результаты в (**), получим:
. Подставляя эти результаты в (**), получим: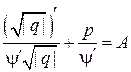 или
или  ,
, . (
. ( )
) . Из (*):
. Из (*):


 ,
, , а
, а 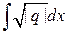 – одна из первообразных от
– одна из первообразных от 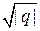 .
.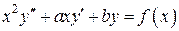 ,
, ,
,  ,
,  ,
, 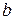 –
–  или
или  – нужная подстановка.
– нужная подстановка. (*)
(*) , то такой цели служит только подстановка
, то такой цели служит только подстановка , где
, где  .
. , преобразующей неизвестную функцию
, преобразующей неизвестную функцию 
 – непрерывные функции по
– непрерывные функции по  ,
,  , …,
, …,  в некоторой области
в некоторой области  , то любой внутренней точке
, то любой внутренней точке  области
области  соответствует, и притом единственное, решение
соответствует, и притом единственное, решение  ,
,  , …,
, …, 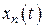 , удовлетворяюще этим начальным условиям. Такое решение называется частным.
, удовлетворяюще этим начальным условиям. Такое решение называется частным. , получим бесконечное множество решений, или:
, получим бесконечное множество решений, или: , …,
, …, 
 (2)
(2) – действительные числа,
– действительные числа,  – известные непрерывные функции. Если
– известные непрерывные функции. Если  , то система называется однородной.
, то система называется однородной. их выражениями из (2):
их выражениями из (2): .
. (*)
(*) , …,
, …,  ,
,  , …,
, …,  (предполагая
(предполагая 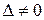 ) и подставляя в
) и подставляя в 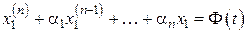 (**)
(**) от него из (*) найдем
от него из (*) найдем  ,
,
 ,
,
 .
. .
.


