
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В силу следствия достаточно найти решение уравнения
но последнее было уже рассмотрено. Из этого следует, что его решение нужно искать в виде
На основании теоремы о наложении решений и следствия из вспомогательной теоремы,
где Снова используем формулы Эйлера:
Приводим
где Замечание. При использовании (**) надо помнить, что вид Пример.
9.4.3. Линейные дифференциальные уравнения, приводящиеся к уравнениям с постоянными коэффициентами
Теорема. Линейное дифференциальное уравнение преобразуется снова в линейное дифференциальное уравнение при всяком линейном преобразовании неизвестной функции и любом преобразовании аргумента (и только при таких преобразованиях). Доказательство. В уравнении
положим
и исходное уравнение преобразуется к виду
и это уравнение снова является линейным, так как все коэффициенты и правая часть есть функции только Положим, что
Подставляя эти значения, получим опять линейное уравнение:
заменяя Предположим теперь, что
Подставляя
Чтобы (*) было линейным, нужно, чтобы
и тогда
есть функция от
Очевидно, что для преобразования линейного дифференциального уравнения с переменными коэффициентами в линйое дифференциальное уравнение с постоянными коэффициентами достаточно рассмотреть соответствующее однородное уравнение.
Согласно теореме, сохранение линейности возможно только в двух случаях: при линейном преобразовании функции Теперь выведем условия, налагаемые на Необходимое и достаточное условие для преобразования Итак, пусть дано уравнение
и подстановка
подставляя в уравнение, получим:
и потребуем, чтобы коэффициенты при
Тогда
Последнее равенство можно записать, как
(3) и есть условие приводимости (1) к (2), в котором коэффициенты являются постоянными. Найдем теперь
Положим
Таким образом, преобразование выполняется, если выполнено (3). Пример.
Условие (3) выполняется и
Необходимое и достаточное условие для преобразования Пусть
Далее,
Из (*), считая
Кроме того,
( Найдем теперь
где Таким образом, если выполняется ( Пример. Рассмотрим уравнение Эйлера
здесь
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 102; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.96.61 (0.021 с.) |
 ,
, ,
,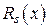 – с неопределенными комплексными коэффициентами,
– с неопределенными комплексными коэффициентами,  – кратность
– кратность 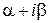 в характеристическом уравнении.
в характеристическом уравнении.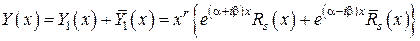 ,
, сопряжен с
сопряжен с  ,
, .
. к виду
к виду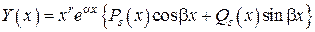 , (**)
, (**) ,
,  – многочлены с вещественными коэффициентами.
– многочлены с вещественными коэффициентами. , но является более полным. Так, если
, но является более полным. Так, если  , то в (**) мы должны брать
, то в (**) мы должны брать  , если
, если  , то в (**) следует взять
, то в (**) следует взять  , и если
, и если  , то в (**) возьмем
, то в (**) возьмем  , и т. д.
, и т. д. ,
, ,
, 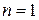 ,
,  ,
,  ,
, , так как
, так как  не корень характеристического уравнения,
не корень характеристического уравнения, ,
, ,
,  ,
,  ,
,  , и т. д.
, и т. д.
 , где
, где  – новая искомая функция, а
– новая искомая функция, а 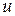 и
и  – известные функции. Тогда
– известные функции. Тогда ,
, ,
,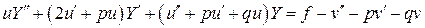 ,
, . отметим, что
. отметим, что  , тогда
, тогда  и
и ,
, 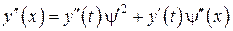 .
. ,
, найдем, что все коэффициенты и правая часть есть функции только
найдем, что все коэффициенты и правая часть есть функции только  . На этом доказательство первой части закончено.
. На этом доказательство первой части закончено. . Тогда
. Тогда ,
, 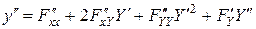 .
. ,
,  и
и  в исходное уравнение, получим в общем случае нелинейное уравнение
в исходное уравнение, получим в общем случае нелинейное уравнение . (*)
. (*) и
и  не зависели от
не зависели от  , а
, а  содержало
содержало  в линейную функцию. Если
в линейную функцию. Если

 ,
, не зависит от
не зависит от 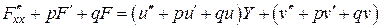
 (
( , так как она не входит в коэффициенты в левой части) и при произвольном преобразовании
, так как она не входит в коэффициенты в левой части) и при произвольном преобразовании  и
и  линейного дифференциального уравнения 2-го порядка, при которых это уравнение может быть приведено к линейному дифференциальному уравнению 2-го порядка с постоянными коэффициентами с помощью преобразования
линейного дифференциального уравнения 2-го порядка, при которых это уравнение может быть приведено к линейному дифференциальному уравнению 2-го порядка с постоянными коэффициентами с помощью преобразования 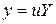 или
или  (1)
(1) ,
, ,
, , (2)
, (2) были константами:
были константами: .
. . Отсюда
. Отсюда  или
или
 или
или .
. , где
, где  . (3)
. (3) , с помощью которой это приведение выполняется:
, с помощью которой это приведение выполняется:

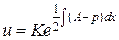 .
. и
и  , тогда
, тогда 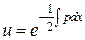 и
и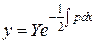 .
. .
. приводит к уравнению
приводит к уравнению .
. и
и 
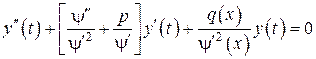 . (
. ( )
)

 , имеем
, имеем 
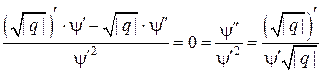 .
. . Подставляя эти результаты в (**), получим:
. Подставляя эти результаты в (**), получим: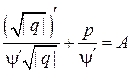 или
или  ,
, . (
. ( )
) . Из (*):
. Из (*):


 ,
, , а
, а 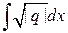 – одна из первообразных от
– одна из первообразных от 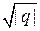 .
.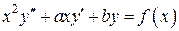 ,
, ,
,  ,
,  ,
, 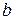 –
– 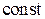 , тогда
, тогда  или
или  – нужная подстановка.
– нужная подстановка.


