
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Д.у. с разделяющимися переменными.
Д.у. с разделяющимися переменными называют такое, что разрешив его относительно
Т.к. Т.е. дифференциалы некоторых функций
Иногда д.у. с разделяющимися переменными может быть в виде: (A)
Пример.
Однако переход от общего интеграла к общему решению не всегда возможен. Замечание. При делении на Если 7.5.2. Однородные д.у. 1-го порядка. Д.у. называется однородным, если, разрешив его относительно (B)
Пример.
Однородные уравнения часто задаются в виде: ( ( ! Признак однородности ( (*) где t – произвольный множитель, k – целое. Положим в (*)
При решении (
Пример.
Замечание. Интегральные кривые однородного уравнения (любого) – семейство подобных кривых с центром подобия в начале координат. Чтобы убедиться в этом достаточно заметить, что изоклины (B) образуют пучок прямых, проходящих через О. Пусть (**) Дополнительно к уравнениям с разделяющимися переменными: Уравнения вида
7.5.3. Линейные уравнения 1-го порядка.
Д.у. 1-го порядка называются линейными, если Для интегрирования применим так называемый метод вариации произвольной постоянной. Проинтегрируем линейное однородное уравнение:
Решение же неоднородного линейного д.у. будим искать в виде т.е. заменим С на u(x), которую необходимо найти. Т.о. константа заменяется переменной функцией, т.е. варьируется. Найдем
Пример.
!!! Рассмотреть метод подстановки -
7.5.4. Уравнение Бернулли. Уравнение вида
т.к. всякое линейное д.у. может быть проинтегрировано в квадратурах, то это справедливо и по отношению к д.у. Бернулли. Практически, для интегрирования д.у. Бернулли нет необходимости предварительно преобразовывать его в линейное. Можно применить метод вариации произвольной постоянной, как и для линейного неоднородного.
Пример.
Его решение
К рассмотренным выше типам д.у. сводятся многие другие с помощью преобразования переменных или перехода к обратной функции. Пример.
В общем случае:
Пример.
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 112; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.181.81 (0.012 с.) |
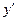 получим для нее:
получим для нее:
 - переменные разделены
- переменные разделены 
 и
и  и сами функции могут отличаться лишь на постоянную величину, то есть
и сами функции могут отличаться лишь на постоянную величину, то есть - общий интеграл.
- общий интеграл. или
или


 возможна “потеря” решений (как в алгебре).
возможна “потеря” решений (как в алгебре). имеет действительные решения
имеет действительные решения  , то прямые
, то прямые  - интегральные кривые д.у.
- интегральные кривые д.у.  - корни
- корни  , и
, и  , где
, где  корни
корни  . В разобранном примере прямые
. В разобранном примере прямые  и
и  являются интегральными и получаются из общего решения при С=0.
являются интегральными и получаются из общего решения при С=0. .
. , которое, заменой переменной
, которое, заменой переменной  преобразуется в уравнение с разделяющимися переменными:
преобразуется в уравнение с разделяющимися переменными:
 - найдя его общее решение и положив в нем
- найдя его общее решение и положив в нем  ,
, 
 или
или  или
или 
 )
)  или
или )
) 








 - есть корни (**). А это ничто иное как уравнения прямых
- есть корни (**). А это ничто иное как уравнения прямых  . Далее, строя приближенные ломанные, убедимся в правильности замечания.
. Далее, строя приближенные ломанные, убедимся в правильности замечания. с помощью подстановки
с помощью подстановки  сводятся к уравнениям с разделяющимися переменными.
сводятся к уравнениям с разделяющимися переменными. и
и 


 и подставим в неоднородное уравнение: после приведения подобных получим:
и подставим в неоднородное уравнение: после приведения подобных получим:
 - общее решение неоднородного линейного д.у. 1-го порядка.
- общее решение неоднородного линейного д.у. 1-го порядка. найти
найти  проходящую через точку
проходящую через точку 

 , n – любое действительное число. При n=0 – линейное неоднородное, n=1 – линейное однородное. Уравнение Бернулли заменой
, n – любое действительное число. При n=0 – линейное неоднородное, n=1 – линейное однородное. Уравнение Бернулли заменой  , где
, где  новая неизвестная функция, преобразуется в линейное относительно z.
новая неизвестная функция, преобразуется в линейное относительно z.
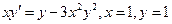 , найдем сначала решение д.у.
, найдем сначала решение д.у.  .
. . Пусть
. Пусть 
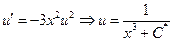 Где
Где  - общее решение
- общее решение - решение задачи Коши,
- решение задачи Коши, 
 заменой
заменой 


 сводится к линейному при переходе к обратной функции:
сводится к линейному при переходе к обратной функции:



