
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные дифференциальные уравнения первого порядка. ⇐ ПредыдущаяСтр 5 из 5
Дифференциальное уравнение первого порядка называется линейным, если оно линейно относительно искомой функции и ее производной. В общем случае линейное уравнение записывается в виде Рассмотрим однородное линейное уравнение Y’+p(x)Y = 0. Это уравнение с разделяющимися переменными которое легко интегрируется Метод вариации произвольной постоянной. Сущность этого метода заключается в том, что постоянную С, входящую в общее решение (1) заменяют функцией от x, т.е. считают Откуда Подставляя (3) в (2), получим общее решение неоднородного уравнения в виде Метод подстановки. В уравнение 18. Системы дифференциальных уравнений с постоянными коэффициентами Рассмотрим систему ДУ: Будем искать решение по методу Эйлера в виде:
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 139; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.113.197 (0.005 с.) |
 , где коэффициенты a(x), b(x) и правая часть f(x) считается заданными функциями на некотором интервале (α, β). Если f(x) ≡ 0 на интервале (α, β), то заданное линейное уравнение называется однородным в том смысле, что тогда левая часть этого уравнения является однородной функцией относительно переменных y и y'. Будем предполагать, что а(х) ≠ 0 на (α, β) и запишем уравнение в виде
, где коэффициенты a(x), b(x) и правая часть f(x) считается заданными функциями на некотором интервале (α, β). Если f(x) ≡ 0 на интервале (α, β), то заданное линейное уравнение называется однородным в том смысле, что тогда левая часть этого уравнения является однородной функцией относительно переменных y и y'. Будем предполагать, что а(х) ≠ 0 на (α, β) и запишем уравнение в виде  где
где  .
. (1) - общее решение уравнения.
(1) - общее решение уравнения. (2) и предполагая что (2) есть решение неоднородного уравнения находят С(х), а вместе с тем и общее решение этого уравнения. Имеем
(2) и предполагая что (2) есть решение неоднородного уравнения находят С(х), а вместе с тем и общее решение этого уравнения. Имеем 
 ,
,  (3), где С – произвольная постоянная.
(3), где С – произвольная постоянная.
 . (4) Выберем v таким образом, чтобы
. (4) Выберем v таким образом, чтобы  . Откуда
. Откуда  , где С – произвольная постоянная. Так как нам достаточно только одного значения v, то будем считать С = 1. Подставляя найденное значение v при C = 1 в уравнение (4) получим дифференциальное уравнение с разделяющимися переменными относительно u
, где С – произвольная постоянная. Так как нам достаточно только одного значения v, то будем считать С = 1. Подставляя найденное значение v при C = 1 в уравнение (4) получим дифференциальное уравнение с разделяющимися переменными относительно u  . Откуда
. Откуда 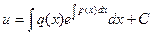 . Зная u и v, можем записать теперь общее решение начального уравнения в виде
. Зная u и v, можем записать теперь общее решение начального уравнения в виде  (1), где
(1), где  -постоянные коэффициенты.
-постоянные коэффициенты. (2), где
(2), где  - постоянные, не все равные нулю, которые следует подобрать, если это возможно так, чтобы функции (2) удовлетворяли системе (1). Подставим (2) в (1). После сокращения на
- постоянные, не все равные нулю, которые следует подобрать, если это возможно так, чтобы функции (2) удовлетворяли системе (1). Подставим (2) в (1). После сокращения на  , получим:
, получим:  (3). Систему уравнений (3) будем рассматривать как однородную систему
(3). Систему уравнений (3) будем рассматривать как однородную систему  -алгебраических уравнений с
-алгебраических уравнений с  (4). Уравнение (4) называется характеристич. уравнением для сист. (1). Уравнение (4) яв-ся алгебраическим уравнением
(4). Уравнение (4) называется характеристич. уравнением для сист. (1). Уравнение (4) яв-ся алгебраическим уравнением 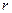 . Нетривиальное решение однородной системы (1) существует тогда и только тогда, когда
. Нетривиальное решение однородной системы (1) существует тогда и только тогда, когда  корень характер. ур-ия (4).
корень характер. ур-ия (4).


