Устойчивость и асимптотическая устойчивость по Ляпунову.
Рассмотрим ДУ:  (1) (1)
Опред. Решение 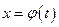 ур-ия называется устойчивым по Ляпунову, при ур-ия называется устойчивым по Ляпунову, при  , если , если 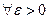  такое, что для всякого решения такое, что для всякого решения  этого уравнения из неравенства этого уравнения из неравенства  (2) следуют неравенство (2) следуют неравенство  (3), при (3), при 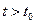 . Если хотя бы для одного решения уравнения (1) из (2) не следует (3) то . Если хотя бы для одного решения уравнения (1) из (2) не следует (3) то  - неустойчивое решение. - неустойчивое решение.
Геометрически устойчивость означает: какой бы не была 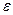 -полоска, содержащая кривую -полоска, содержащая кривую 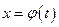 , достаточно близкие к ней в начальный момент времени , достаточно близкие к ней в начальный момент времени  интегральные кривые интегральные кривые  уравнения (1) целиком содержатся в указанной уравнения (1) целиком содержатся в указанной 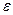 -полоске при всех -полоске при всех  . .
Решение 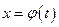 уравнения (1) называется асимптотически устойчивым, если 1) оно устойчиво и 2) уравнения (1) называется асимптотически устойчивым, если 1) оно устойчиво и 2) 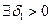 такое, что для любого решения такое, что для любого решения  уравнения (1), удовлетворяющего условию уравнения (1), удовлетворяющего условию  имеем имеем 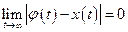 . .
Исследовать на устойчивость тривиальное  решение уравнений: решение уравнений:
Пример 1. 
 Решение. Решение уравнения, удовл. нач. условию Решение. Решение уравнения, удовл. нач. условию  , имеет вид , имеет вид  . Покажем, что для произвольного фиксированного . Покажем, что для произвольного фиксированного  и и 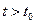 не существует положительного не существует положительного  такого, что из условия такого, что из условия  следует следует  . Действительно, если при любом фиксированном . Действительно, если при любом фиксированном  : :  , то , то 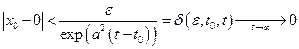 . Т.е. . Т.е. 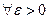 не существует такого не существует такого  , чтобы выполнялось условие устойчивости , чтобы выполнялось условие устойчивости
тривиального решения.
Пример 2. 
 Решение. Общее решение уравнения имеет вид: Решение. Общее решение уравнения имеет вид:  . Тривиальное решение удовлетворяет нач. условию . Тривиальное решение удовлетворяет нач. условию 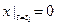 . След-но, . След-но, 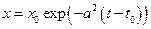 -решение уравнения, удовлет. нач. усл-ию -решение уравнения, удовлет. нач. усл-ию  . Имеем при . Имеем при 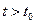 : :  . Если примем . Если примем  , то из условия , то из условия  следует следует  . По определению, это означает, что решение . По определению, это означает, что решение  устойчивое. Кроме того, устойчивое. Кроме того, 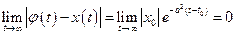 . Т.е. тривиальное решение асимптот. устойчиво. . Т.е. тривиальное решение асимптот. устойчиво.
 Пример 3. Пример 3. 
Решение.  -общее решение уравнения. Решение -общее решение уравнения. Решение  удовлет. нач. условию удовлет. нач. условию  . Решение . Решение  , удовлет. нач. условию , удовлет. нач. условию  имеет вид: имеет вид:  . В этом случае . В этом случае 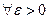  такое, что такое, что  , если , если  для всех для всех  . Следовательно, . Следовательно,  устойчивое решение уравнения. устойчивое решение уравнения.
Асимптотической устойчивости здесь нет, так как прямая  не стремится к прямой не стремится к прямой  при при  . .
9. Оценка погрешности метода последовательных приближений для уравнения  . .
Рассмотрим ДУ: 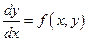 с НУ: с НУ: 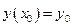 . Метод последовательных приближений имеет вид: . Метод последовательных приближений имеет вид:  . Считая выполненными условия теоремы существования и единственности решения, получим оценку метода последовательных приближений. Пусть . Считая выполненными условия теоремы существования и единственности решения, получим оценку метода последовательных приближений. Пусть  . Обозначим через . Обозначим через 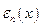 -погрешность -погрешность  -го приближенного решения -го приближенного решения 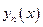 к решению к решению  и воспользуемся условием Липшица: и воспользуемся условием Липшица:
 (*). Т.е. зная погрешность (*). Т.е. зная погрешность  -го приближения, можно получить оценку погрешности -го приближения, можно получить оценку погрешности  -го приближения. Имеем, используя теорему Лагранжа: -го приближения. Имеем, используя теорему Лагранжа:  , где , где  . По формуле (*), находим: . По формуле (*), находим:
 . Методом мат. индукции получаем оценку . Методом мат. индукции получаем оценку  -го приближ. решения: -го приближ. решения:  . .
Пример. Методом послед. приближений найти второе приближение к решению задачи Коши: 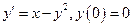 в квадрате в квадрате  . .
Решение. Ф-ия  непрерывна вместе со своей производной непрерывна вместе со своей производной  в рассматриваемом квадрате в рассматриваемом квадрате  . Поэтому . Поэтому  удовлетворяет условию Липшица с постоянной удовлетворяет условию Липшица с постоянной 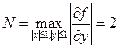 . Так как . Так как  , то , то  . Следовательно, пикаровские приближения сходятся по крайней мере в промежутке . Следовательно, пикаровские приближения сходятся по крайней мере в промежутке  . Приближения вычисляем по формуле: . Приближения вычисляем по формуле: 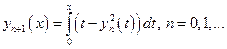 . Имеем: . Имеем:  . Разность м/у точным решением и найденным вторым последовательным приближением: . Разность м/у точным решением и найденным вторым последовательным приближением:
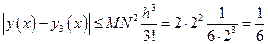 . Таким образом, теорема существования и единственности гарантирует сходимость последовательных приближений на интервале . Таким образом, теорема существования и единственности гарантирует сходимость последовательных приближений на интервале  . Погрешность второго приближения . Погрешность второго приближения 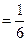 . .
10. Решение систем ДУ методом исключения.
Рассмотрим систему ДУ: 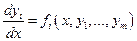 (1). Метод исключения заключается в следующем: из уравнений системы (1) и из уравнений, получающихся дифференцированием уравнений, входящих в систему, исключаем все неизвестные функции, кроме одной, для определения которой получаем одно ДУ порядка выше первого. Интегрируя это уравнение, находим одну из неизвестных функций, а остальные неизвестные функции по возможности без интегрирования получаем из исходных в результате дифференцирования найденной первой неизвестной функции. (1). Метод исключения заключается в следующем: из уравнений системы (1) и из уравнений, получающихся дифференцированием уравнений, входящих в систему, исключаем все неизвестные функции, кроме одной, для определения которой получаем одно ДУ порядка выше первого. Интегрируя это уравнение, находим одну из неизвестных функций, а остальные неизвестные функции по возможности без интегрирования получаем из исходных в результате дифференцирования найденной первой неизвестной функции.
Пример. 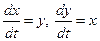 . .
Решение. Дифференцируем первое уравнение системы:  . Подставляем второе уравнение системы: . Подставляем второе уравнение системы:  . Откуда, получаем решение: . Откуда, получаем решение:  . Из первого уравнения системы дифференцированием найденного значения получаем: . Из первого уравнения системы дифференцированием найденного значения получаем:  . .
11. Структура общего решения линейной однородной системы ДУ с непрерыв. на  коэф. коэф.
Рассмотрим систему: 
Теорема. Линейная комбинация  фундаментальной системы решений фундаментальной системы решений  однородной системы ДУ (1) с непр. на однородной системы ДУ (1) с непр. на  коэф. есть общее решение этой системы на коэф. есть общее решение этой системы на  . .
Док-во. Так как коэф. системы (1) непрерывны на  , то эта система имеет единственное решение на , то эта система имеет единственное решение на  , удовлет. произвольно заданным нач. условиям. Составим функцию , удовлет. произвольно заданным нач. условиям. Составим функцию  (2). При любых постоянных (2). При любых постоянных  она является решением системы (1). Произвольно зададим начальные условия она является решением системы (1). Произвольно зададим начальные условия  . В силу равенства (2) имеем: . В силу равенства (2) имеем: 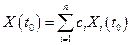 или в развернутом виде: или в развернутом виде:  . Получили неоднородную систему линейных алгебраических уравнений относительно неизвестных . Получили неоднородную систему линейных алгебраических уравнений относительно неизвестных  , определитель которой есть , определитель которой есть  . Следовательно, эта система имеет единственное решение . Следовательно, эта система имеет единственное решение  . Это означает, что решение . Это означает, что решение  , опред. рав-ом (2), есть общее решение системы (1). , опред. рав-ом (2), есть общее решение системы (1).
Опред. Векторы  называются линейно-зависимыми на называются линейно-зависимыми на  , если существуют постоянные , если существуют постоянные  , не все равные нулю, такие, что , не все равные нулю, такие, что  (*) на (*) на  . Если тожд. (*) справедливо только при . Если тожд. (*) справедливо только при  , то вектор-функции наз-ся линейно независимыми. , то вектор-функции наз-ся линейно независимыми.
Теорема. Если вектор-функции  линейно зависимы на линейно зависимы на  , то определитель , то определитель  на на  . .
Теорема. Для того, чтобы частные решения  системы (1) были линейно независимы на системы (1) были линейно независимы на  , необходимо и достаточно, чтобы опред. Вронского , необходимо и достаточно, чтобы опред. Вронского  не обращался в нуль ни в одной точке отрезка не обращался в нуль ни в одной точке отрезка  . .
Опред. Система  линейно независимых решений линейно независимых решений  системы (1) наз-ся фундаментальной системой решений на системы (1) наз-ся фундаментальной системой решений на  . .
Опред. Система  функций функций  (**), зависящая от (**), зависящая от  и и  произвольных постоянных произвольных постоянных  называется общим решением системы (1) в нек. области называется общим решением системы (1) в нек. области  существования и единственности задачи Коши, если: 1) При любых допустимых значениях существования и единственности задачи Коши, если: 1) При любых допустимых значениях  система функций (**) обращает систему ДУ в тождество; 2) какими бы ни были нач. условия система функций (**) обращает систему ДУ в тождество; 2) какими бы ни были нач. условия  существуют постоянные существуют постоянные  , такие, что , такие, что  . Решение, полученное из общего при конкретных значениях постоянных . Решение, полученное из общего при конкретных значениях постоянных  наз-ся частным решением. наз-ся частным решением.
Пример. 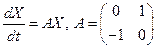 . .
Решение. Ищем решение в виде:  . Подставив в исходную систему, получим: . Подставив в исходную систему, получим:  . Характеристическое уравнение . Характеристическое уравнение  имеет корни имеет корни  . При . При  , получаем: , получаем: 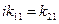 . Приняв . Приняв 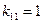 , имеем , имеем 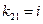 . То есть . То есть  , ,  . Таким образом, общее решение системы имеет вид: . Таким образом, общее решение системы имеет вид: 
Так как, вронскиан  , то решения , то решения  и и 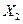 -линейно независимы. -линейно независимы.
12. Уравнение Бернулли. Метод решения.
Уравнением Бернулли называется уравнение 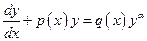 (1), где (1), где  . Уравнение (1) при . Уравнение (1) при  -однородное линейное уравнение, при -однородное линейное уравнение, при  -неоднородное линейное уравнение. Поэтому будем предполагать в дальнейшем, что -неоднородное линейное уравнение. Поэтому будем предполагать в дальнейшем, что  и и  . Для . Для  нецелого будем считать нецелого будем считать  . Уравнение Бернулли имеет очевидное решение . Уравнение Бернулли имеет очевидное решение  . Считая . Считая  , разделим обе части уравнения (1) на , разделим обе части уравнения (1) на 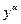 : :  (2) и введем замену (2) и введем замену  . Тогда . Тогда  и уравнение (2) записывается в виде: и уравнение (2) записывается в виде:  . Это линейное однородное уравнение первого порядка относительно . Это линейное однородное уравнение первого порядка относительно  . Его общее решение имеет вид: . Его общее решение имеет вид:  Возвращаясь к переменной Возвращаясь к переменной  , получаем: , получаем:  - общий интеграл уравнения Бернулли. - общий интеграл уравнения Бернулли.
Пример. Решить уравнение  . .
Решение. Разделим уравнение на  , получим: , получим:  (*). Положим (*). Положим  . Тогда . Тогда  . Подставляя в (*), получим: . Подставляя в (*), получим:  или или 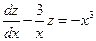 . Т.о. получили линейное уравнение первого порядка, решение которого имеет вид: . Т.о. получили линейное уравнение первого порядка, решение которого имеет вид:  - общее решение. - общее решение.
13. Особые решения ДУ 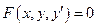 (*). Найти особые решения ур-ия Клеро (*). Найти особые решения ур-ия Клеро  . .
Особые решения – это решения, в каждой точке которых нарушена единственность решения. В точках особого множества одновременно должны выполняться условия: 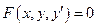 и и  (1). Эти условия являются необходимыми условиями существования особого решения ДУ. Обычно условия (1) записываются в виде: (1). Эти условия являются необходимыми условиями существования особого решения ДУ. Обычно условия (1) записываются в виде: 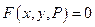 и и  (2). Кривая (2). Кривая  , полученная исключением параметра , полученная исключением параметра  из (2), называется из (2), называется  - дискриминантной кривой. Если какая-либо ветвь - дискриминантной кривой. Если какая-либо ветвь   -дискриминантной кривой яв-ся интегральной кривой ДУ (*), причем в каждой ее точке нарушена единственность решения, то -дискриминантной кривой яв-ся интегральной кривой ДУ (*), причем в каждой ее точке нарушена единственность решения, то  -особое решение ур-ия (*). -особое решение ур-ия (*).
Ур-ие Клеро имеет вид:  . Полагая . Полагая  , получаем , получаем  . Откуда дифференцируя по . Откуда дифференцируя по  , находим: , находим:  . Здесь . Здесь  или или  . В первом случае, исключая . В первом случае, исключая  из уравнений из уравнений  и и  , получаем общее решение , получаем общее решение  (3). Если (3). Если  , то , то  . В этом случае решения определяются из уравнений: . В этом случае решения определяются из уравнений:  (4). Интегральная кривая, определенная уравнениями (4) яв-ся огибающей семейства интегральных прямых (3). Действительно, огибающая некоторого семейства (4). Интегральная кривая, определенная уравнениями (4) яв-ся огибающей семейства интегральных прямых (3). Действительно, огибающая некоторого семейства  определяется уравнениями определяется уравнениями  и и 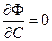 , которые для сем-ва (3) имеют вид , которые для сем-ва (3) имеют вид  и только обозначением параметра отличаются от (4). и только обозначением параметра отличаются от (4).
 Пример. Пример.  . Заменяя в уравнении . Заменяя в уравнении  на произвольную постоянную на произвольную постоянную  , получаем общее решение , получаем общее решение  (**). Кроме того, интегральной кривой яв-ся огибающая семейства (**). Она определяется из ур-ий: (**). Кроме того, интегральной кривой яв-ся огибающая семейства (**). Она определяется из ур-ий:  . Исключая . Исключая  , получаем , получаем  , т.е. огибающую семейства прямых (**). , т.е. огибающую семейства прямых (**).
Найдем особые решения: 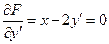 и и  . Откуда . Откуда  - яв-ся решением, а т.к. огибающая, то единственность нарушается, следовательно яв-ся особым решением. - яв-ся решением, а т.к. огибающая, то единственность нарушается, следовательно яв-ся особым решением.
14. Решение неоднородной системы линейных ДУ методом вариации произвольной постоянной.
Рассмотрим неоднородную систему линейных ДУ:  (1) с непрерывными на (1) с непрерывными на  коэффициентами коэффициентами  и функциями и функциями 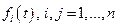 . Покажем, что если известно общее решение соответствующей однородной системы . Покажем, что если известно общее решение соответствующей однородной системы  (2), то общее решение системы можно определить методом вариации произвольной постоянной. Пусть (2), то общее решение системы можно определить методом вариации произвольной постоянной. Пусть  - общее решение системы (2), где - общее решение системы (2), где  - фундаментальная система решений этого уравнения. Решение системы (1) будем искать в виде: - фундаментальная система решений этого уравнения. Решение системы (1) будем искать в виде:  (3), где (3), где  -неизвестные функции от -неизвестные функции от  . Подставляя (3) в (1) и учитывая, что . Подставляя (3) в (1) и учитывая, что  , получаем: , получаем:  (4). Равенство (4) при каждом фиксированном (4). Равенство (4) при каждом фиксированном  представляет собой систему линейных неоднородных алгебраических уравнений относительно неизвестных представляет собой систему линейных неоднородных алгебраических уравнений относительно неизвестных 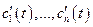 . Определитель этой системы есть . Определитель этой системы есть 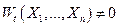 при любом при любом  . Следовательно, система (4) имеет единственное решение: . Следовательно, система (4) имеет единственное решение: 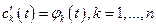 . Откуда . Откуда  , где , где  -произвольные постоянные. Подставляя найденные значения в (3), определим общее решение системы (1): -произвольные постоянные. Подставляя найденные значения в (3), определим общее решение системы (1):  . .
Пример.  (*). (*).
Решение. Общее решение соответствующей однородной системы имеет вид:

Решение системы (*) будем искать в виде:  . Подставляя эти значения . Подставляя эти значения  и и  в систему (*), получаем: в систему (*), получаем:

Откуда находим  , где , где  -произв. постоянные. -произв. постоянные.
Общее решение системы (*) имеет вид:

16. Дифференциальные уравнения порядка выше первого. Методы понижения порядка.
Рассмотрим некоторые виды ДУ:
1)  . Полагаем . Полагаем  , так, чтобы , так, чтобы  . Так как . Так как  , то , то  . Откуда . Откуда  . .
 и т.д. и т.д.
2)  . В этом случае порядок уравнения может быть понижен до порядка . В этом случае порядок уравнения может быть понижен до порядка  заменой заменой 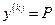 , т.е. введением новой неизвестной функции. После такой замены уравнение примет вид: , т.е. введением новой неизвестной функции. После такой замены уравнение примет вид:  . Допустим, что мы сумели найти общий интеграл уравнения . Допустим, что мы сумели найти общий интеграл уравнения  , или , или 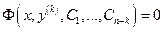 . Последнее уравнение принадлежит к виду . Последнее уравнение принадлежит к виду  , которое интегрируется в квадратурах. , которое интегрируется в квадратурах.
3)  . Порядок уравнения можно понизить на единицу, если за независимую переменную принять . Порядок уравнения можно понизить на единицу, если за независимую переменную принять  , полагая , полагая  , где , где  -новая неизвестная функция. В этом случае все производные -новая неизвестная функция. В этом случае все производные 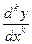 можно выразить через производные функции можно выразить через производные функции  по по  и т.о. понизить порядок уравнения на единицу. Действительно, и т.о. понизить порядок уравнения на единицу. Действительно, 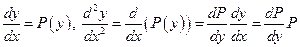 , ,
 и т.д. и т.д.
Подставляя эти значения производных, получим уравнение, порядок которого не единицу ниже исходного.
4) Левая часть уравнения  есть однородная функция аргументов есть однородная функция аргументов  измерения измерения  , т.е. , т.е.  . В этом случае порядок может быть понижен на 1 с помощью подстановки: . В этом случае порядок может быть понижен на 1 с помощью подстановки:  , где , где  -неизвестная ф-ия. Тогда -неизвестная ф-ия. Тогда
 . Подставляя эти значения в исходное уравнение, получаем: . Подставляя эти значения в исходное уравнение, получаем:  . .
Пример 1. 
Решение. Полагаем  . Тогда . Тогда  и исходное уравнение примет вид: и исходное уравнение примет вид:  . Разделяем переменные: . Разделяем переменные:  или или  . Интегрируя, получаем: . Интегрируя, получаем:  или или  , откуда , откуда  . Тогда . Тогда  . .
Пример 2.  (*) (*)
Решение. Полагаем  . Тогда . Тогда 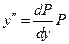 . Уравнение записывается в виде: . Уравнение записывается в виде:  (**). Если (**). Если  , то , то  - общее решение уравнения (**). При - общее решение уравнения (**). При  , получаем , получаем  . Откуда находим общий интеграл уравнения (*): . Откуда находим общий интеграл уравнения (*):  . При . При  : :  , входит в решение , входит в решение  . .
|



 (1)
(1)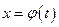 ур-ия называется устойчивым по Ляпунову, при
ур-ия называется устойчивым по Ляпунову, при  , если
, если 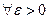
 такое, что для всякого решения
такое, что для всякого решения  этого уравнения из неравенства
этого уравнения из неравенства  (2) следуют неравенство
(2) следуют неравенство  (3), при
(3), при 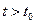 . Если хотя бы для одного решения уравнения (1) из (2) не следует (3) то
. Если хотя бы для одного решения уравнения (1) из (2) не следует (3) то  - неустойчивое решение.
- неустойчивое решение.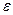 -полоска, содержащая кривую
-полоска, содержащая кривую  интегральные кривые
интегральные кривые  .
.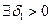 такое, что для любого решения
такое, что для любого решения  имеем
имеем 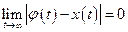 .
. решение уравнений:
решение уравнений:
 Решение. Решение уравнения, удовл. нач. условию
Решение. Решение уравнения, удовл. нач. условию  , имеет вид
, имеет вид  . Покажем, что для произвольного фиксированного
. Покажем, что для произвольного фиксированного  и
и  такого, что из условия
такого, что из условия  следует
следует  . Действительно, если при любом фиксированном
. Действительно, если при любом фиксированном  , то
, то 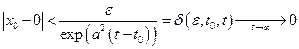 . Т.е.
. Т.е.  , чтобы выполнялось условие устойчивости
, чтобы выполнялось условие устойчивости
 Решение. Общее решение уравнения имеет вид:
Решение. Общее решение уравнения имеет вид:  . Тривиальное решение удовлетворяет нач. условию
. Тривиальное решение удовлетворяет нач. условию  . След-но,
. След-но, 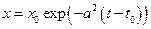 -решение уравнения, удовлет. нач. усл-ию
-решение уравнения, удовлет. нач. усл-ию  . Если примем
. Если примем  , то из условия
, то из условия 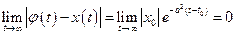 . Т.е. тривиальное решение асимптот. устойчиво.
. Т.е. тривиальное решение асимптот. устойчиво. Пример 3.
Пример 3. 
 -общее решение уравнения. Решение
-общее решение уравнения. Решение  . Решение
. Решение  . В этом случае
. В этом случае  , если
, если  не стремится к прямой
не стремится к прямой  при
при  .
.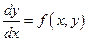 с НУ:
с НУ: 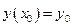 . Метод последовательных приближений имеет вид:
. Метод последовательных приближений имеет вид:  . Считая выполненными условия теоремы существования и единственности решения, получим оценку метода последовательных приближений. Пусть
. Считая выполненными условия теоремы существования и единственности решения, получим оценку метода последовательных приближений. Пусть  . Обозначим через
. Обозначим через 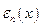 -погрешность
-погрешность  -го приближенного решения
-го приближенного решения 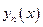 к решению
к решению  и воспользуемся условием Липшица:
и воспользуемся условием Липшица: (*). Т.е. зная погрешность
(*). Т.е. зная погрешность  -го приближения, можно получить оценку погрешности
-го приближения, можно получить оценку погрешности  , где
, где  . По формуле (*), находим:
. По формуле (*), находим: . Методом мат. индукции получаем оценку
. Методом мат. индукции получаем оценку  .
.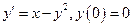 в квадрате
в квадрате  .
. непрерывна вместе со своей производной
непрерывна вместе со своей производной  в рассматриваемом квадрате
в рассматриваемом квадрате  удовлетворяет условию Липшица с постоянной
удовлетворяет условию Липшица с постоянной 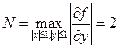 . Так как
. Так как  , то
, то  . Следовательно, пикаровские приближения сходятся по крайней мере в промежутке
. Следовательно, пикаровские приближения сходятся по крайней мере в промежутке  . Приближения вычисляем по формуле:
. Приближения вычисляем по формуле: 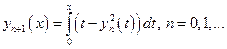 . Имеем:
. Имеем:  . Разность м/у точным решением и найденным вторым последовательным приближением:
. Разность м/у точным решением и найденным вторым последовательным приближением: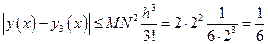 . Таким образом, теорема существования и единственности гарантирует сходимость последовательных приближений на интервале
. Таким образом, теорема существования и единственности гарантирует сходимость последовательных приближений на интервале 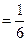 .
.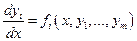 (1). Метод исключения заключается в следующем: из уравнений системы (1) и из уравнений, получающихся дифференцированием уравнений, входящих в систему, исключаем все неизвестные функции, кроме одной, для определения которой получаем одно ДУ порядка выше первого. Интегрируя это уравнение, находим одну из неизвестных функций, а остальные неизвестные функции по возможности без интегрирования получаем из исходных в результате дифференцирования найденной первой неизвестной функции.
(1). Метод исключения заключается в следующем: из уравнений системы (1) и из уравнений, получающихся дифференцированием уравнений, входящих в систему, исключаем все неизвестные функции, кроме одной, для определения которой получаем одно ДУ порядка выше первого. Интегрируя это уравнение, находим одну из неизвестных функций, а остальные неизвестные функции по возможности без интегрирования получаем из исходных в результате дифференцирования найденной первой неизвестной функции.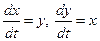 .
. . Подставляем второе уравнение системы:
. Подставляем второе уравнение системы:  . Откуда, получаем решение:
. Откуда, получаем решение:  . Из первого уравнения системы дифференцированием найденного значения получаем:
. Из первого уравнения системы дифференцированием найденного значения получаем:  .
. коэф.
коэф.
 фундаментальной системы решений
фундаментальной системы решений  однородной системы ДУ (1) с непр. на
однородной системы ДУ (1) с непр. на  (2). При любых постоянных
(2). При любых постоянных  она является решением системы (1). Произвольно зададим начальные условия
она является решением системы (1). Произвольно зададим начальные условия  . В силу равенства (2) имеем:
. В силу равенства (2) имеем: 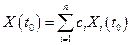 или в развернутом виде:
или в развернутом виде:  . Получили неоднородную систему линейных алгебраических уравнений относительно неизвестных
. Получили неоднородную систему линейных алгебраических уравнений относительно неизвестных  . Следовательно, эта система имеет единственное решение
. Следовательно, эта система имеет единственное решение  . Это означает, что решение
. Это означает, что решение  , опред. рав-ом (2), есть общее решение системы (1).
, опред. рав-ом (2), есть общее решение системы (1). называются линейно-зависимыми на
называются линейно-зависимыми на  , не все равные нулю, такие, что
, не все равные нулю, такие, что  (*) на
(*) на  , то вектор-функции наз-ся линейно независимыми.
, то вектор-функции наз-ся линейно независимыми. на
на  не обращался в нуль ни в одной точке отрезка
не обращался в нуль ни в одной точке отрезка  (**), зависящая от
(**), зависящая от  и
и  существования и единственности задачи Коши, если: 1) При любых допустимых значениях
существования и единственности задачи Коши, если: 1) При любых допустимых значениях  существуют постоянные
существуют постоянные  , такие, что
, такие, что  . Решение, полученное из общего при конкретных значениях постоянных
. Решение, полученное из общего при конкретных значениях постоянных 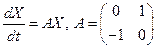 .
. . Подставив в исходную систему, получим:
. Подставив в исходную систему, получим:  . Характеристическое уравнение
. Характеристическое уравнение  имеет корни
имеет корни  . При
. При  , получаем:
, получаем: 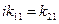 . Приняв
. Приняв 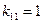 , имеем
, имеем 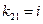 . То есть
. То есть  ,
,  . Таким образом, общее решение системы имеет вид:
. Таким образом, общее решение системы имеет вид: 
 , то решения
, то решения  и
и 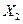 -линейно независимы.
-линейно независимы.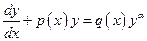 (1), где
(1), где  . Уравнение (1) при
. Уравнение (1) при  -однородное линейное уравнение, при
-однородное линейное уравнение, при  -неоднородное линейное уравнение. Поэтому будем предполагать в дальнейшем, что
-неоднородное линейное уравнение. Поэтому будем предполагать в дальнейшем, что  и
и  . Для
. Для  нецелого будем считать
нецелого будем считать  . Уравнение Бернулли имеет очевидное решение
. Уравнение Бернулли имеет очевидное решение  . Считая
. Считая  , разделим обе части уравнения (1) на
, разделим обе части уравнения (1) на 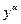 :
:  (2) и введем замену
(2) и введем замену  . Тогда
. Тогда  и уравнение (2) записывается в виде:
и уравнение (2) записывается в виде:  . Это линейное однородное уравнение первого порядка относительно
. Это линейное однородное уравнение первого порядка относительно  . Его общее решение имеет вид:
. Его общее решение имеет вид:  Возвращаясь к переменной
Возвращаясь к переменной  , получаем:
, получаем:  - общий интеграл уравнения Бернулли.
- общий интеграл уравнения Бернулли. .
. , получим:
, получим:  (*). Положим
(*). Положим  . Тогда
. Тогда  . Подставляя в (*), получим:
. Подставляя в (*), получим:  или
или 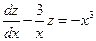 . Т.о. получили линейное уравнение первого порядка, решение которого имеет вид:
. Т.о. получили линейное уравнение первого порядка, решение которого имеет вид:  - общее решение.
- общее решение.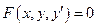 (*). Найти особые решения ур-ия Клеро
(*). Найти особые решения ур-ия Клеро  .
. (1). Эти условия являются необходимыми условиями существования особого решения ДУ. Обычно условия (1) записываются в виде:
(1). Эти условия являются необходимыми условиями существования особого решения ДУ. Обычно условия (1) записываются в виде: 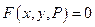 и
и  (2). Кривая
(2). Кривая  , полученная исключением параметра
, полученная исключением параметра  из (2), называется
из (2), называется 
 . Полагая
. Полагая  , получаем
, получаем  . Откуда дифференцируя по
. Откуда дифференцируя по  , находим:
, находим:  . Здесь
. Здесь  или
или  . В первом случае, исключая
. В первом случае, исключая  , получаем общее решение
, получаем общее решение  (3). Если
(3). Если  . В этом случае решения определяются из уравнений:
. В этом случае решения определяются из уравнений:  (4). Интегральная кривая, определенная уравнениями (4) яв-ся огибающей семейства интегральных прямых (3). Действительно, огибающая некоторого семейства
(4). Интегральная кривая, определенная уравнениями (4) яв-ся огибающей семейства интегральных прямых (3). Действительно, огибающая некоторого семейства  определяется уравнениями
определяется уравнениями 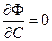 , которые для сем-ва (3) имеют вид
, которые для сем-ва (3) имеют вид  и только обозначением параметра отличаются от (4).
и только обозначением параметра отличаются от (4). Пример.
Пример.  на произвольную постоянную
на произвольную постоянную  , получаем общее решение
, получаем общее решение  (**). Кроме того, интегральной кривой яв-ся огибающая семейства (**). Она определяется из ур-ий:
(**). Кроме того, интегральной кривой яв-ся огибающая семейства (**). Она определяется из ур-ий:  . Исключая
. Исключая  , т.е. огибающую семейства прямых (**).
, т.е. огибающую семейства прямых (**).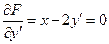 и
и  . Откуда
. Откуда  - яв-ся решением, а т.к. огибающая, то единственность нарушается, следовательно яв-ся особым решением.
- яв-ся решением, а т.к. огибающая, то единственность нарушается, следовательно яв-ся особым решением. (1) с непрерывными на
(1) с непрерывными на  и функциями
и функциями 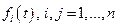 . Покажем, что если известно общее решение соответствующей однородной системы
. Покажем, что если известно общее решение соответствующей однородной системы  - общее решение системы (2), где
- общее решение системы (2), где  (3), где
(3), где  -неизвестные функции от
-неизвестные функции от  , получаем:
, получаем:  (4). Равенство (4) при каждом фиксированном
(4). Равенство (4) при каждом фиксированном 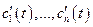 . Определитель этой системы есть
. Определитель этой системы есть 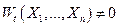 при любом
при любом  . Следовательно, система (4) имеет единственное решение:
. Следовательно, система (4) имеет единственное решение: 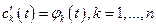 . Откуда
. Откуда  , где
, где  -произвольные постоянные. Подставляя найденные значения в (3), определим общее решение системы (1):
-произвольные постоянные. Подставляя найденные значения в (3), определим общее решение системы (1):  .
. (*).
(*).
 . Подставляя эти значения
. Подставляя эти значения  и
и  в систему (*), получаем:
в систему (*), получаем:
 , где
, где  -произв. постоянные.
-произв. постоянные.
 . Полагаем
. Полагаем  , так, чтобы
, так, чтобы  . Так как
. Так как  , то
, то  . Откуда
. Откуда  .
. и т.д.
и т.д. . В этом случае порядок уравнения может быть понижен до порядка
. В этом случае порядок уравнения может быть понижен до порядка  заменой
заменой 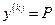 , т.е. введением новой неизвестной функции. После такой замены уравнение примет вид:
, т.е. введением новой неизвестной функции. После такой замены уравнение примет вид:  . Допустим, что мы сумели найти общий интеграл уравнения
. Допустим, что мы сумели найти общий интеграл уравнения  , или
, или 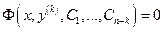 . Последнее уравнение принадлежит к виду
. Последнее уравнение принадлежит к виду  , которое интегрируется в квадратурах.
, которое интегрируется в квадратурах. . Порядок уравнения можно понизить на единицу, если за независимую переменную принять
. Порядок уравнения можно понизить на единицу, если за независимую переменную принять  , где
, где 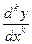 можно выразить через производные функции
можно выразить через производные функции 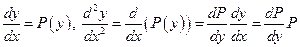 ,
, и т.д.
и т.д. есть однородная функция аргументов
есть однородная функция аргументов  измерения
измерения  , т.е.
, т.е.  . В этом случае порядок может быть понижен на 1 с помощью подстановки:
. В этом случае порядок может быть понижен на 1 с помощью подстановки:  , где
, где  -неизвестная ф-ия. Тогда
-неизвестная ф-ия. Тогда . Подставляя эти значения в исходное уравнение, получаем:
. Подставляя эти значения в исходное уравнение, получаем:  .
.
 . Тогда
. Тогда  и исходное уравнение примет вид:
и исходное уравнение примет вид:  . Разделяем переменные:
. Разделяем переменные:  или
или  . Интегрируя, получаем:
. Интегрируя, получаем:  или
или  , откуда
, откуда  . Тогда
. Тогда  .
. (*)
(*)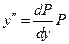 . Уравнение записывается в виде:
. Уравнение записывается в виде:  (**). Если
(**). Если  , то
, то  - общее решение уравнения (**). При
- общее решение уравнения (**). При  . Откуда находим общий интеграл уравнения (*):
. Откуда находим общий интеграл уравнения (*):  . При
. При  :
:  , входит в решение
, входит в решение