
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Устойчивость автономных систем (Продолжение)
Пример 1.
Пример 2. Решение. Матрица коэффициентов системы При При Таким образом, решение системы имеет вид:
6. Уравнения, неразрешенные относительно производной вида
Пример. Решение. Положим
Пример. Решение. Полагаем Теорема существования и единственности решения задачи Коши. Рассмотрим дифференциальное уравнение Теорема. Пусть выполнены следующие условия: 1) f(x, y) – непрерывная функция двух переменных в замкнутой области D = {x0 - a ≤ x ≤ x0 + a; y0 – b ≤ b ≤ y0 + b}, где a и b – положительные числа и
2) Функция f(x, y) удовлетворяет в области D относительно переменной условию Липшеца. Это означает, что существует такое положительное число N, для любого x из интервала |x – x0| ≤ a и любых значений y1, y2 из интервала |y – y0| ≤ b, выполняется неравенство |f(x, y1) – f(x, y2)| ≤ N|y1 – y2|. (4) Тогда существует единственное решение y = y(x) задачи Коши (1), (2), определенное на интервале x0 - h ≤ x ≤ x0 + h, где
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 117; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.165.66 (0.005 с.) |
 .
. Решение. Матрица коэффициентов системы
Решение. Матрица коэффициентов системы  . Харак-ое уравнение
. Харак-ое уравнение  имеет корни
имеет корни  .Следовательно, точка покоя (0,0) – неустойчивый узел. Исследуем поведение траекторий системы в окрестности точки (0,0). Перейдем к однородному уравнению:
.Следовательно, точка покоя (0,0) – неустойчивый узел. Исследуем поведение траекторий системы в окрестности точки (0,0). Перейдем к однородному уравнению:  .
.  - интегральные кривые этого уравнения. Откуда следует, что траекториями исходной системы являются лучи на координатных осях, движение по которым идет от начала координат, и семейство ветвей парабол, касающихся начала координат.
- интегральные кривые этого уравнения. Откуда следует, что траекториями исходной системы являются лучи на координатных осях, движение по которым идет от начала координат, и семейство ветвей парабол, касающихся начала координат.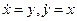
 . Решение системы будем искать в виде:
. Решение системы будем искать в виде:  и
и  . Для определения
. Для определения  получаем систему:
получаем систему:  (*). Определитель системы
(*). Определитель системы 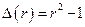 . Следовательно, характеристическое уравнение
. Следовательно, характеристическое уравнение  имеет корни
имеет корни  . Поэтому, точка покоя (0,0) – седло.
. Поэтому, точка покоя (0,0) – седло. , из (*) получаем:
, из (*) получаем:  . Следовательно,
. Следовательно, 
 , из (*) получаем:
, из (*) получаем:  . Следовательно,
. Следовательно, 
 (**). Найдем решение в виде первого интеграла. Имеем:
(**). Найдем решение в виде первого интеграла. Имеем:  .
. Положим в (**)
Положим в (**)  . Тогда
. Тогда  . То есть траекториями системы являются два луча, выходящие из начала координат с угловым коэф.
. То есть траекториями системы являются два луча, выходящие из начала координат с угловым коэф.  . При
. При  имеем
имеем  . Т.е. два луча, входящие в начало координат с угловым коэф.
. Т.е. два луча, входящие в начало координат с угловым коэф.  являются траекториями системы.
являются траекториями системы. . Указать метод решения. Решить уравнения а)
. Указать метод решения. Решить уравнения а)  , б)
, б)  .
. (1). Если заданное уравнение трудно разрешить относительно
(1). Если заданное уравнение трудно разрешить относительно  , то бывает целесообразным ввести параметр
, то бывает целесообразным ввести параметр  и заменить заданное уравнение двумя уравнениями
и заменить заданное уравнение двумя уравнениями  и
и  ,
,  , где функции
, где функции  выбираются так, чтобы
выбираются так, чтобы  при
при  , то
, то  . Откуда получаем:
. Откуда получаем:  . Если ур-ие (1) легко разрешить относительно
. Если ур-ие (1) легко разрешить относительно  , т.е.
, т.е.  , то почти всегда удобно в качестве параметра взять
, то почти всегда удобно в качестве параметра взять  . Тогда:
. Тогда: 
 . Тогда
. Тогда  . Из уравнений
. Из уравнений 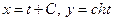 легко исключить параметр
легко исключить параметр 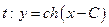 .
. (2). Если уравнение (2) трудно разрешить относительно
(2). Если уравнение (2) трудно разрешить относительно  , где
, где  ,
,  . Если (2) легко разрешить относ-но
. Если (2) легко разрешить относ-но  , то берем
, то берем  и
и  .
. . Тогда
. Тогда  .
.  Интегрируя, получаем:
Интегрируя, получаем:  .
. (1) с начальными условиями y(x0) = y0 (2)
(1) с начальными условиями y(x0) = y0 (2)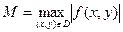 . (3)
. (3)



