Устойчивость автономных систем.
Рассмотрим систему дифференциальных уравнений:  (1), где функции
(1), где функции  определены для всех
определены для всех  и
и  из некоторой области
из некоторой области  и удовлетворяют условиям теоремы существования и единственности решения задачи Коши в некоторой замкнутой окрестности
и удовлетворяют условиям теоремы существования и единственности решения задачи Коши в некоторой замкнутой окрестности  точки
точки  .
.
Опред. Решение 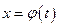 системы диф. ур-ий называется устойчивым по Ляпунову, при
системы диф. ур-ий называется устойчивым по Ляпунову, при  , если
, если 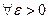
 такое, что для всякого решения
такое, что для всякого решения  системы из неравенств
системы из неравенств  (2) следуют неравенства
(2) следуют неравенства  (3),
(3),  при
при 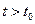 . Если хотя бы для одного решения системы (1) из (2) не следует (3) при всех
. Если хотя бы для одного решения системы (1) из (2) не следует (3) при всех  , то
, то  - неустойчивое решение системы. Решение
- неустойчивое решение системы. Решение 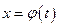 системы (1) называется асимптотически устойчивым, если оно устойчиво и
системы (1) называется асимптотически устойчивым, если оно устойчиво и  ,
, 
Рассмотрим автономную системы 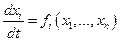 ,
,  (4), для которой
(4), для которой  . Это значит, что точка
. Это значит, что точка  есть точка покоя системы (4), а следовательно, точка
есть точка покоя системы (4), а следовательно, точка  .
.
Обозначим ч/з  шар
шар  . Будем предполагать, что правые части системы (4) в
. Будем предполагать, что правые части системы (4) в  удовлетворяют условиям теоремы существования и единственности решения задачи Коши.
удовлетворяют условиям теоремы существования и единственности решения задачи Коши.
Опред. Точка покоя системы дифференциальных уравнений (4) называется устойчивой, если 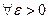
 , что любая траектория системы (4), начинающаяся в момент времени
, что любая траектория системы (4), начинающаяся в момент времени  в точке
в точке 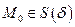 , все время затем остается в шаре
, все время затем остается в шаре  .
.
Опред. Точка покоя системы (4) наз-ся асимптотически устойчивой, если: 1) она устойчива и 2) 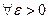
 , что каждая траектория системы (4), начинающаяся в момент времени
, что каждая траектория системы (4), начинающаяся в момент времени  в точке
в точке 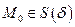 , стремится к точке покоя, когда время
, стремится к точке покоя, когда время  бесконечно возрастает.
бесконечно возрастает.
Рас-им систему ДУ:  (5). Будем считать, что
(5). Будем считать, что  . Это означ., что система имеет единственную точку покоя
. Это означ., что система имеет единственную точку покоя  . Исследуем поведение траекторий в окрестности этой точки. Решение системы будем искать в виде:
. Исследуем поведение траекторий в окрестности этой точки. Решение системы будем искать в виде:  . Для определения
. Для определения  получаем систему:
получаем систему:  . Система имеет ненулевое решение, когда
. Система имеет ненулевое решение, когда  . Харак-ое уравнение м\б составлено по матрице системы
. Харак-ое уравнение м\б составлено по матрице системы  :
:  . Тогда решение системы имеет вид:
. Тогда решение системы имеет вид:  (6). Рассмотрим случаи:
(6). Рассмотрим случаи:
1) Корни  характер. ур-ия действительные и различные
характер. ур-ия действительные и различные
1. Пусть  . Устойчивый узел (асимптотическая устойчивость). Предположим, что
. Устойчивый узел (асимптотическая устойчивость). Предположим, что  . Тогда
. Тогда  . Это означает, что траек-ми. сист. (5) яв-ся два луча, входящие в нач. коор. с угловым коэф.
. Это означает, что траек-ми. сист. (5) яв-ся два луча, входящие в нач. коор. с угловым коэф.  . При
. При  получаем еще два луча, вход. в нач. коор. под углом
получаем еще два луча, вход. в нач. коор. под углом  . В общем случае
. В общем случае  , что означает, что все траек-ии (за искл. лучей с угл. коэф.
, что означает, что все траек-ии (за искл. лучей с угл. коэф.  ) имеют направ. лучей
) имеют направ. лучей  .
.
2. Пусть  . Неустойчивый узел
. Неустойчивый узел
3. Пусть  . Седло (точка покоя неустойчива). При
. Седло (точка покоя неустойчива). При  получаем два луча
получаем два луча  , выходящие из начала координат (т.к.
, выходящие из начала координат (т.к.  ). При
). При  - два луча
- два луча  , входящие в начало координат. В общем случае:
, входящие в начало координат. В общем случае:  . Т.е. траектории удаляются от начала координат при
. Т.е. траектории удаляются от начала координат при  по направлению лучей
по направлению лучей  .
.
2) Корни  - комплексные, т.е.
- комплексные, т.е.  . а)
. а)  - устойчивый фокус, б)
- устойчивый фокус, б)  - неустойчивый фокус, в)
- неустойчивый фокус, в)  - центр
- центр
3) Корни  - кратные. Вырожденный узел.
- кратные. Вырожденный узел.
3) Корни  - кратные. Вырожденный узел.
- кратные. Вырожденный узел.
Устойчивость автономных систем.
Рассмотрим систему дифференциальных уравнений:  (1), где функции
(1), где функции  определены для всех
определены для всех  и
и  из некоторой области
из некоторой области  и удовлетворяют условиям теоремы существования и единственности решения задачи Коши в некоторой замкнутой окрестности
и удовлетворяют условиям теоремы существования и единственности решения задачи Коши в некоторой замкнутой окрестности  точки
точки  .
.
Опред. Решение 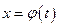 системы диф. ур-ий называется устойчивым по Ляпунову, при
системы диф. ур-ий называется устойчивым по Ляпунову, при  , если
, если 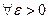
 такое, что для всякого решения
такое, что для всякого решения  системы из неравенств
системы из неравенств  (2) следуют неравенства
(2) следуют неравенства  (3),
(3),  при
при 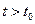 . Если хотя бы для одного решения системы (1) из (2) не следует (3) при всех
. Если хотя бы для одного решения системы (1) из (2) не следует (3) при всех  , то
, то  - неустойчивое решение системы. Решение
- неустойчивое решение системы. Решение 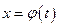 системы (1) называется асимптотически устойчивым, если оно устойчиво и
системы (1) называется асимптотически устойчивым, если оно устойчиво и  ,
, 
Рассмотрим автономную системы 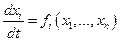 ,
,  (4), для которой
(4), для которой  . Это значит, что точка
. Это значит, что точка  есть точка покоя системы (4), а следовательно, точка
есть точка покоя системы (4), а следовательно, точка  .
.
Обозначим ч/з  шар
шар  . Будем предполагать, что правые части системы (4) в
. Будем предполагать, что правые части системы (4) в  удовлетворяют условиям теоремы существования и единственности решения задачи Коши.
удовлетворяют условиям теоремы существования и единственности решения задачи Коши.
Опред. Точка покоя системы дифференциальных уравнений (4) называется устойчивой, если 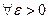
 , что любая траектория системы (4), начинающаяся в момент времени
, что любая траектория системы (4), начинающаяся в момент времени  в точке
в точке 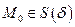 , все время затем остается в шаре
, все время затем остается в шаре  .
.
Опред. Точка покоя системы (4) наз-ся асимптотически устойчивой, если: 1) она устойчива и 2) 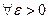
 , что каждая траектория системы (4), начинающаяся в момент времени
, что каждая траектория системы (4), начинающаяся в момент времени  в точке
в точке 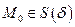 , стремится к точке покоя, когда время
, стремится к точке покоя, когда время  бесконечно возрастает.
бесконечно возрастает.
Рас-им систему ДУ:  (5). Будем считать, что
(5). Будем считать, что  . Это означ., что система имеет единственную точку покоя
. Это означ., что система имеет единственную точку покоя  . Исследуем поведение траекторий в окрестности этой точки. Решение системы будем искать в виде:
. Исследуем поведение траекторий в окрестности этой точки. Решение системы будем искать в виде:  . Для определения
. Для определения  получаем систему:
получаем систему:  . Система имеет ненулевое решение, когда
. Система имеет ненулевое решение, когда  . Харак-ое уравнение м\б составлено по матрице системы
. Харак-ое уравнение м\б составлено по матрице системы  :
:  . Тогда решение системы имеет вид:
. Тогда решение системы имеет вид:  (6). Рассмотрим случаи:
(6). Рассмотрим случаи:
1) Корни  характер. ур-ия действительные и различные
характер. ур-ия действительные и различные
1. Пусть  . Устойчивый узел (асимптотическая устойчивость). Предположим, что
. Устойчивый узел (асимптотическая устойчивость). Предположим, что  . Тогда
. Тогда  . Это означает, что траек-ми. сист. (5) яв-ся два луча, входящие в нач. коор. с угловым коэф.
. Это означает, что траек-ми. сист. (5) яв-ся два луча, входящие в нач. коор. с угловым коэф.  . При
. При  получаем еще два луча, вход. в нач. коор. под углом
получаем еще два луча, вход. в нач. коор. под углом  . В общем случае
. В общем случае  , что означает, что все траек-ии (за искл. лучей с угл. коэф.
, что означает, что все траек-ии (за искл. лучей с угл. коэф.  ) имеют направ. лучей
) имеют направ. лучей  .
.
2. Пусть  . Неустойчивый узел
. Неустойчивый узел
3. Пусть  . Седло (точка покоя неустойчива). При
. Седло (точка покоя неустойчива). При  получаем два луча
получаем два луча  , выходящие из начала координат (т.к.
, выходящие из начала координат (т.к.  ). При
). При  - два луча
- два луча  , входящие в начало координат. В общем случае:
, входящие в начало координат. В общем случае:  . Т.е. траектории удаляются от начала координат при
. Т.е. траектории удаляются от начала координат при  по направлению лучей
по направлению лучей  .
.
2) Корни  - комплексные, т.е.
- комплексные, т.е.  . а)
. а)  - устойчивый фокус, б)
- устойчивый фокус, б)  - неустойчивый фокус, в)
- неустойчивый фокус, в)  - центр
- центр
3) Корни  - кратные. Вырожденный узел.
- кратные. Вырожденный узел.
3) Корни  - кратные. Вырожденный узел.
- кратные. Вырожденный узел.


 (1), где функции
(1), где функции  определены для всех
определены для всех  и
и  из некоторой области
из некоторой области  и удовлетворяют условиям теоремы существования и единственности решения задачи Коши в некоторой замкнутой окрестности
и удовлетворяют условиям теоремы существования и единственности решения задачи Коши в некоторой замкнутой окрестности  точки
точки  .
.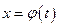 системы диф. ур-ий называется устойчивым по Ляпунову, при
системы диф. ур-ий называется устойчивым по Ляпунову, при  , если
, если 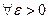
 такое, что для всякого решения
такое, что для всякого решения  системы из неравенств
системы из неравенств  (2) следуют неравенства
(2) следуют неравенства  (3),
(3),  при
при 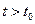 . Если хотя бы для одного решения системы (1) из (2) не следует (3) при всех
. Если хотя бы для одного решения системы (1) из (2) не следует (3) при всех  - неустойчивое решение системы. Решение
- неустойчивое решение системы. Решение  ,
, 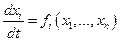 ,
,  . Это значит, что точка
. Это значит, что точка  есть точка покоя системы (4), а следовательно, точка
есть точка покоя системы (4), а следовательно, точка  .
. шар
шар  . Будем предполагать, что правые части системы (4) в
. Будем предполагать, что правые части системы (4) в  в точке
в точке 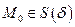 , все время затем остается в шаре
, все время затем остается в шаре  .
. бесконечно возрастает.
бесконечно возрастает. (5). Будем считать, что
(5). Будем считать, что  . Это означ., что система имеет единственную точку покоя
. Это означ., что система имеет единственную точку покоя  . Исследуем поведение траекторий в окрестности этой точки. Решение системы будем искать в виде:
. Исследуем поведение траекторий в окрестности этой точки. Решение системы будем искать в виде:  . Для определения
. Для определения  получаем систему:
получаем систему:  . Система имеет ненулевое решение, когда
. Система имеет ненулевое решение, когда  . Харак-ое уравнение м\б составлено по матрице системы
. Харак-ое уравнение м\б составлено по матрице системы  :
:  . Тогда решение системы имеет вид:
. Тогда решение системы имеет вид:  (6). Рассмотрим случаи:
(6). Рассмотрим случаи: характер. ур-ия действительные и различные
характер. ур-ия действительные и различные . Устойчивый узел (асимптотическая устойчивость). Предположим, что
. Устойчивый узел (асимптотическая устойчивость). Предположим, что  . Тогда
. Тогда  . Это означает, что траек-ми. сист. (5) яв-ся два луча, входящие в нач. коор. с угловым коэф.
. Это означает, что траек-ми. сист. (5) яв-ся два луча, входящие в нач. коор. с угловым коэф.  . При
. При  получаем еще два луча, вход. в нач. коор. под углом
получаем еще два луча, вход. в нач. коор. под углом  . В общем случае
. В общем случае  , что означает, что все траек-ии (за искл. лучей с угл. коэф.
, что означает, что все траек-ии (за искл. лучей с угл. коэф.  .
. . Неустойчивый узел
. Неустойчивый узел . Седло (точка покоя неустойчива). При
. Седло (точка покоя неустойчива). При  , выходящие из начала координат (т.к.
, выходящие из начала координат (т.к.  ). При
). При  . Т.е. траектории удаляются от начала координат при
. Т.е. траектории удаляются от начала координат при  . а)
. а)  - устойчивый фокус, б)
- устойчивый фокус, б)  - неустойчивый фокус, в)
- неустойчивый фокус, в)  - центр
- центр


