
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Доказательство существования решения.
Докажем сначала что решение задачи (1), (2) равносильно решению интегрального уравнения В самом деле пусть y = y(x) – решение задачи Коши (1), (2) в некоторой окрестности точки x0. Тогда в этой окрестности имеет место тождество При доказательстве существования решения уравнения (5) будем пользоваться методом последовательных приближений (методом Пикара). За нулевое последовательное приближение к решению возьмем произвольно заданное число y0, n-ое последовательное приближение определим по формуле Сначала докажем, применяя метод математической индукции. Что ни одно из последовтельных приближений не выходит из области D. Если x0 - h ≤ x ≤ x0 + h, где Рассмотрим первое приближение Так как функция под знаком интеграла известна, то y1(x) вычисляется квадратурой. Если ограничить изменение х в формуле (9) интервалом | x - x0 | ≤ h, то значения аргументов x и y0 функции, а будут принадлежать области D, в которой выполнено условие (3). Из формулы (9) получаем |y1(x) – y0| ≤ M|x –x0| ≤ Mh ≤ M Тогда из равенства Покажем что существует предел полученных последовательных приближений {yn(x)} и что этот предел удовлетворяет интегральному уравнению (5), а следовательно и задаче (1), (2). Для этого достаточно показать сходимость ряда y0 + (y1(x) – y0) + (y2(x) – y1(x)) + … (10) так как частная сумма этого ряда Sn(x) = yn(x). Имеем Таким образом, доказано, что ряд (10) на сегменте В сходимости ряда (11) легко убедится применяя признаки Даламбера. Это означает по теореме Вейерштрасса, что ряд (10) сходится на сегменте Следовательно
При
Докажем что Используя условия Липшица и сходимость последовательности {yn(x)} к пределу y(x), имеем Переходя в (12) к пределу при Доказательство единственности Допустим что кроме решения y(x) задачи (1), (2) существуют по крайней мере ещё одно решение z(x) этой задачи. В этом случае имеем Без ограничения общности будем предполагать, что значения x, для которых y(x) ≠ z(x) находятся вправо от точки х0 на некотором достаточно малом интервале (x0, x0 + ε), где ε > 0. В противном случае за точку x0 можно взять другую точку, в любой близости которой y(x) ≠ z(x) или заменить х на –х. Функция | y(x) - z(x) | непрерывна на отрезке [x0, x0 + ε], следовательно, на этом отрезке она достигает своего наибольшего значения в некоторой точке ξ ≠ x0. Обозначим
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 165; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.70.203 (0.005 с.) |
 (5)
(5) (6). Интегрируя это тождество в пределах от х0 до х и учитывая условие (2) получаем
(6). Интегрируя это тождество в пределах от х0 до х и учитывая условие (2) получаем  (7) т.е. решение задачи (1), (2) удовлетворяет интегральному уравнению (5)
(7) т.е. решение задачи (1), (2) удовлетворяет интегральному уравнению (5) (8)
(8)
 (9)
(9) = b, т.е. y1(x) не выходит из области D. Предположим теперь что yn-1(x)не выходит из области D при
= b, т.е. y1(x) не выходит из области D. Предположим теперь что yn-1(x)не выходит из области D при 
 находим |yn(x) – y0| ≤ Mh ≤ b при
находим |yn(x) – y0| ≤ Mh ≤ b при  Используя неравенство Липшица и полученную оценку разности | y1(x) – y0 |, находим
Используя неравенство Липшица и полученную оценку разности | y1(x) – y0 |, находим  Применяя метод математической индукции, получаем, что для всех n = 1, 2, … справедливая оценка
Применяя метод математической индукции, получаем, что для всех n = 1, 2, … справедливая оценка 
 мажорируется сходящимся числовым рядом
мажорируется сходящимся числовым рядом  (11)
(11)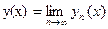 - непрерывная функция на сегменте
- непрерывная функция на сегменте 
 , если
, если  (12)
(12) при
при 
 . Существование решения задачи Коши (1), (2) доказано.
. Существование решения задачи Коши (1), (2) доказано.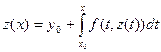
 , где θ – не равна нулю. В силу условия Липшица имеем
, где θ – не равна нулю. В силу условия Липшица имеем  или 1 ≤ Nε. Так как ε можно выбрать как угодно малым, например, взять
или 1 ≤ Nε. Так как ε можно выбрать как угодно малым, например, взять  , то приходим к противоречию 1 < 1. Следовательно, решение задачи Коши (1), (2) единственное.
, то приходим к противоречию 1 < 1. Следовательно, решение задачи Коши (1), (2) единственное.


