
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аналитические методы плазовых работСодержание книги
Поиск на нашем сайте
2.5.1. На рис. 2.24 приведена плоская деталь – кильсон, плоскость которого перпендикулярна ОП и наклонена к ДП и ПМШ. При аналитическом определении его размеров, все пересекающие кильсон шпангоуты аппроксимируются соответствующими уравнениями так же, как и теоретическая линия притыкания кильсона – линия пересечения его плоскости с внутренней поверхностью наружной обшивки. Совместное решение этих уравнений позволяет определить координаты у и z точек, а, с, d, e, b. Вычтя координаты z этих точек из zД, можно найти величину отрезков hi=zД-z. Растянутая шпация 2.5.2. Если деталь наклонена ко всем трём основным плоскостям корпуса судна (рис. 2.25), координаты точек а, с, d, e, b находят как и в предыдущем случае. Линии пересечения кильсона плоскостями шпангоутов параллельны друг другу. Необходимо вычислить sin α по формуле:
тогда
По этим данным можно однозначно задать контур и размеры кильсона. 2.5.3. Детали двоякой кривизны аналитически разворачивают методом наименьших площадей. Поверхность детали апроксимируют многогранной поверхностью (рис. 2.26). Рёбрами поверхности являются отрезки, соединяющие точки разбиения шпангоутов, а гранями – треугольники (способ триангуляции). Все шпангоуты апроксимируют кубическими полиномами с коэффициентами Ai, Bi, Ci, Di, определяемыми при решении системы:
где y1, z1, …, yi, zi, …, yn, zn – координаты точек в координатах Ozyx; z'1, z"n – величины вторых производных в пазовых точках, получаемые при решении задачи трассировки пазов. Длину i-го шпангоута между ВП и НП вычисляют по формуле:
где z'шп – первая производная уравнения, которым апроксимирован шпангоут.
Этой же формулой пользуются для вычисления длины средних линий шпангоутных полос, равных сумме длин образующих их дуг шпангоутов. Из всех полос выбирают полосу с максимальной длиной средней линии и разделяют её на N частей, состоящих из двух треугольников каждая. Обычно принимают N=10 (на рис. 2.21) для упрощения принято N=5. Для определения координат у точек разбиения шпангоутов указанной полосы, равных верхнему пределу интеграла (2.12), при длинах дуг si=li/10; …; 9li/10 также используют формулу (2.12). III. лабораторный практикум
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 638; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.230.165 (0.007 с.) |


 , где
, где  ; уа и уb – полушироты точек а и b. Зная hi и РШ, можно построить контур кильсона.
; уа и уb – полушироты точек а и b. Зная hi и РШ, можно построить контур кильсона. ,
,
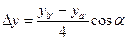 ;
;  ;
;  .
.


 ,
,




