Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системный подход в моделировании системСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Классический (или индуктивный) подход к моделированию рассматривает систему, переходя от частного к общему, и синтезирует ее путем слияния компонент, разрабатываемых отдельно. Системный подход предполагает последовательный переход от общего к частному, когда в основе рассмотрения лежит цель, при этом объект выделяется из окружающего мира. При создании нового объекта с полезными свойствами (например, системы управления) задаются критерии, определяющие степень полезности полученных свойств. Так как любой объект моделирования представляет собой систему взаимосвязанных элементов, введем понятие системы. Система S есть целенаправленное множество взаимосвязанных элементов любой природы. Внешняя среда. Е представляет собой множество существующих вне системы элементов любой природы, оказывающих влияние на систему или находящихся под ее воздействием. При системном подходе к моделированию прежде всего четко определяется цель моделирования. Создание модели полного аналога оригинала дело трудоемкое и дорогое, поэтому модель создается под определенную цель. Важным для системного подхода является определение структуры системы — совокупности связей между элементами системы, отражающих их взаимодействие. Существует ряд походов к исследованию систем и ее свойств, к которым следует отнести структурный и функциональный. При структурном подходе выявляется состав выделенных элементов системы S и связи между ними. Совокупность элементов и связей позволяет судить о свойствах выделенной части системы. При функциональном подходе рассматриваются функции (алгоритмы) поведения системы, причем, каждая функция описывает поведение одного свойства при внешнем воздействии Е. Такой подход не требует знания структуры системы, а ее описание состоит из набора функций ее реакции на внешние воздействия. Классический метод построения модели использует функциональный подход, при котором в качестве элемента модели принимается компонента, описывающая поведение одного свойства и не отображающая реальный состав элементов. Кроме этого компоненты системы являются изолированными друг от друга, что плохо отражает моделируемую систему. Такой метод построения модели применим лишь для простых систем, так как требует включения в состав функций, описывающих свойства системы, отношения между свойствами, которые могут быть плохо определены или неизвестны. С усложнением моделируемых систем, когда невозможно учесть все взаимовлияния свойств, применяется системный метод, основанный на структурном подходе. При этом система S разбивается на ряд подсистем Sl со своими свойствами, которые, естественно, проще описать функциональными зависимостями, и определяются связи между подсистемами. В этом случае система функционирует в соответствии со свойствами отдельных подсистем и связей между ними. Это избавляет от необходимости описывать функционально взаимосвязи между свойствами системы S, делает модель более гибкой, так как изменение свойств одной из подсистем автоматически изменяет свойства системы.
Классификация видов моделирования В зависимости от характера изучаемых процессов в системе S и цели моделирования существует множество типов моделей и способов их классификации, например, по цели использования, наличию случайных воздействий, отношению ко времени, возможности реализации, области применения и др. (таблица 14).
Таблица 14. Типы моделей
По цели использования модели классифицируются на научный эксперимент, в котором осуществляется исследование модели с применением различных средств получения данных об объекте, возможности влияния на ход процесса, с целью получения новых данных об объекте или явлении; комплексные испытания и производственный эксперимент, использующие натурное испытание физического объекта для получения высокой достоверности о его характеристиках; оптимизационные, связанные с нахождением оптимальных показателей системы (например, нахождение минимальных затрат или определение максимальной прибыли). По наличию воздействий на систему модели делятся на детерминированные (в системах отсутствуют случайные воздействия) и стохастические (в системах присутствуют вероятностные воздействия). Эти же модели некоторые авторы классифицируют по способу оценки параметров системы: в детерминированных системах параметры модели оцениваются одним показателем для конкретных значений их исходных данных; в стохастических системах наличие вероятностных характеристик исходных данных позволяет оценивать параметры системы несколькими показателями. По отношению ко времени модели разделяют на статические, описывающие систему в определенный момент времени, и динамические, рассматривающие поведение системы во времени. В свою очередь, динамические модели подразделяют на дискретные, в которых все события происходят по интервалам времени, и непрерывные, где все события происходят непрерывно во времени. По возможности реализации модели классифицируются как мысленные, описывающие систему, которую трудно или невозможно моделировать реально, реальные, в которых модель системы представлена либо реальным объектом, либо его частью, и информационные, реализующие информационные процессы (возникновение, передачу, обработку и использование информации) на компьютере. В свою очередь, мысленные модели разделяют на наглядные (при которых моделируемые процессы и явления протекают наглядно); символические (модель системы представляет логический объект, в котором основные свойства и отношения реального объекта выражены системой знаков или символов) и математические (представляют системы математических объектов, позволяющие получать исследуемые характеристики реального объекта). Реальные модели делят на натурные (проведение исследования на реальном объекте и последующая обработка результатов эксперимента с применением теории подобия) и физические (проведение исследования на установках, которые сохраняют природу явления и обладают физическим подобием). По области применения модели подразделяют на универсальные, предназначенные для использования многими системами, и специализированные, созданные для исследования конкретной системы.
Математические модели Наиболее важным этапом при построении модели является переход от содержательного описания к формальному, что объясняется участием на этом этапе специалистов в предметной области, где существует моделируемая система, и специалистов в области моделирования систем. Наиболее удобным языком для их общения, целью которого является построение адекватной модели системы, обычно, является язык математических описаний. Математическое описание системы компактно и удобно для дальнейших реализаций на компьютере, с целью проведения статистических испытаний,
Примеры построения динамических моделей При моделировании непрерывных динамических объектов в качестве моделей обычно выступают дифференциальные уравнения, связывающее поведение объекта со временем. Положительным свойством дифференциальных уравнений является то, что одно и то же уравнение моделирует системы различной физической природы. В качестве независимой переменной в динамических системах обычно выступает время, от которого зависят неизвестные значения искомой функции, определяющие поведения объекта. Математическое описание модели в общем виде:
где Например, процесс малых колебаний маятника описывается обыкновенным дифференциальным уравнением
Процесс в электрическом колебательном контуре Очевидно, что если положить
Общая математическая модель позволяет исследовать одну систему, моделируя работу другой. Модели динамических систем на основе дифференциальных уравнений нашли широкое применение в теории управления различными техническими объектами. Под влиянием неизвестных заранее возмущений фактическое поведение системы отклоняется от желаемого, задаваемого алгоритмом и для приближения ее поведения к необходимому значению, в состав системы вводится автоматическое управление системой. Оно может быть встроено в саму систему, но при моделировании блок управления отделяется от самой системы. В общем виде структура многомерной системы автоматического управления (САУ) представлена на рис. 3.
Рисунок 3. Структура многомерной системы автоматического управления.
Информационные модели Информационные модели во многих случаях опираются на математические модели, так как при решении задач математическая модель исследуемого объекта, процесса или явления неизбежно преобразуется в информационную для ее реализации на компьютере. Определим основные понятия информационной модели. Информационным объектом называется описание реального объекта, процесса или явления в виде совокупности его характеристик (информационных элементов), называемых реквизитами. Информационный объект определенной структуры (реквизитного состава) образует тип (класс), которому присваивают уникальное имя. Информационный объект с конкретными характеристиками называют экземпляром. Каждый экземпляр идентифицируется заданием ключевого реквизита (ключа). Одни и те же реквизиты в различных информационных объектах могут быть как ключевыми, так и описательными. Информационный объект может иметь несколько ключей. Пример. Информационный объект СТУДЕНТ имеет реквизитный состав: номер (номер зачетной книжки — ключевой реквизит), фамилия, имя, отчество, дата рождения, код места обучения. Информационный объект ЛИЧНОЕ ДЕЛО: номер студента, домашний адрес, номер аттестата о среднем образовании, семейное положение, дети. Информационный объект МЕСТО ОБУЧЕНИЯ включает реквизиты: код (ключевой реквизит), наименование вуза, факультет, группа. Информационный объект ПРЕПОДАВАТЕЛЬ: код (ключевой реквизит), кафедра, фамилия, имя, отчество, ученая степень, ученое звание, должность. Отношения, существующие между реальными объектами, определяются в информационных моделях как связи. Существует три вида связей: один к одному (1:1), один ко многим (1:∞) и многие ко многим ( ∞: ∞ ). Связь один к одному определяет соответствие одному экземпляру информационного объекта X не более одного экземпляра информационного объекта Y, и наоборот. Пример. Информационные объекты СТУДЕНТ и ЛИЧНОЕ ДЕЛО будут связаны отношением один к одному. Каждый студент имеет определенные уникальные данные в личном деле. При связи один ко многим одному экземпляру информационного объекта X может соответствовать любое количество экземпляров информационного объекта Y, но каждый экземпляр объекта Y связан не более чем с одним экземпляром объекта X. Пример. Между информационными объектами МЕСТО ОБУЧЕНИЯ и СТУДЕНТ необходимо установить связь один ко многим. Одно и то же место обучения может многократно повторяться для различных студентов. Связь многие ко многим предполагает соответствие одному экземпляру информационного объекта X любое количество экземпляров объекта Y, и наоборот. Пример. Информационные объекты СТУДЕНТ и ПРЕПОДАВАТЕЛЬ имеют связь многие ко многим. Каждый студент обучается у множества преподавателей, а каждый преподаватель учит множество студентов.
Примеры информационных моделей Определим информационную модель как связанную совокупность информационных объектов, описывающих информационные процессы в исследуемой предметной области. Существующие информационные модели разделим на универсальные и специализированные. Универсальные модели предназначены для использования в различных предметных областях, к ним относятся: базы данных и системы управления базами данных, автоматизированные системы управления, базы знаний, экспертные системы. Специализированные модели предназначены для описания конкретных систем, являются уникальными по своим возможностям, более дорогостоящими. Универсальные модели. Базы данных Базы данных представляют связанную совокупность структурированных данных, относящихся к определенному процессу или явлению, в конкретной предметной области. Система управления базами данных представляет собой программный комплекс для создания, организации необходимой обработки, хранения и передачи баз данных. Ядром любой БД является модель представления данных. Модель данных представляет множество структур данных и взаимосвязи между ними. Различают иерархическую, сетевую и реляционную модели данных. Иерархическая модель представляет связи между объектами (данными) в виде дерева. К основным понятиям иерархической модели относятся: • узел — набор атрибутов данных, описывающих объект; • связь — линия, связывающая узлы нижнего уровня с одним узлом вышележащего уровня. При этом узел вышележащего уровня называют предком для соответствующих ему узлов нижнего уровня, в свою очередь, узлы нижнего уровня называют потомками связанного с ними вышележащего узла (например, на рис. 4. узел В1 — предок для узлов CI, С2, а узлы С1, С2 — потомки узла В1); • уровень — номер слоя узлов, отсчитанный от корня.
Рисунок 4. Иерархическая модель данных
Количество деревьев в БД определяется числом корневых записей. К каждому узлу существует единственный путь от корня. Сетевая структура имеет те же составляющие, что и иерархическая, но каждый узел может быть связан с любым другим узлом (рис. 5). Сетевой подход к организации данных является расширением иерархического. В иерархических моделях запись-потомок должна иметь только одного предка; в сетевых — потомок может иметь любое число предков.
Рисунок 5. Сетевая модель данных
Обе эти модели не получили широкого распространения из-за сложности реализации графов в виде машинных структур данных, кроме того, в них сложно осуществить операции поиска информации. Набольшее распространение получила третья модель данных — реляционная, она может так же описывать иерархическую и сетевую модель. Реляционная модель ориентирована на организацию данных в виде двумерных таблиц.
Искусственный интеллект Идеи моделирования человеческого разума известны с древнейших времен. Впервые об этом упоминается в сочинении философа и теолога Раймунда Луллия (ок.1235 — ок.1315) «Великое искусство», который не только высказал идею логической машины для решения разнообразных задач, исходя из всеобщей классификации понятий (XIV в.), но и попытался ее реализовать. Рене Декарт (1596-1650) и Готфрид Вильгельм Лейбниц (1646—1716) независимо друг от друга развивали учение о прирожденной способности ума к познанию и всеобщих и необходимых истин логики и математики, работали над созданием универсального языка классификации всех знаний. Именно на этих идеях базируются теоретические основы создания искусственного интеллекта. Толчком к дальнейшему развитию модели человеческого мышления стало появление в 40-х гг. XX в. ЭВМ. В 1948 г. американский ученый Норберт Винер (1894-1964) сформулировал основные положения новой науки — кибернетики. В 1956 г. в Стенфордском университете (США) на семинаре под названием «Artificial intelligence* (искусственный интеллект), посвященном решению логических задач, признано новое научное направление, связанное с машинным моделированием человеческих интеллектуальных функций и названное искусственный интеллект. Вскоре эта отрасль разделилась на два основных направления: нейрокибернетику и кибернетику «черного ящика». Нейрокибернетика обратилась к структуре человеческого мозга как единственно мыслящему объекту и занялась его аппаратным моделированием. Физиологи давно выявили нейроны — связанные друг с другом нервные клетки как основу мозга. Нейрокибернетика занимается созданием элементов, аналогичных нейронам, и их объединением в функционирующие системы, эти системы называют нейросетями. В середине 80-х гг. XX в.в Японии был создан первый нейрокомпьютер, моделирующий структуру человеческого мозга. Его основная область применения — распознавание образов. Кибернетика «черного ящика» использует другие принципы, структура модели не главное, важна ее реакция на заданные входные данные, на выходе модель должна реагировать как человеческий мозг. Ученые этого направления занимаются разработкой алгоритмов решения интеллектуальных задач для имеющихся вычислительных систем. Наиболее значимые результаты: • Модель лабиринтного поиска (конец 50-х гг.), в которой рассматривается граф состояний объекта и в нем происходит поиск оптимального пути от входных данных к результирующим. На практике эта модель не нашла широкого применения. • Эвристическое программирование (начало 60-х гг.) разрабатывало стратегии действий на основе заранее известных заданных правил (эвристик). Эвристика — теоретически не обоснованное правило, позволяющее уменьшить количество переборов в поиске оптимального пути. • Методы математической логики. Метод резолюций, позволяющий на основе определенных аксиом автоматически доказывать теоремы. В 1973 г. создан язык логического программирования Пролог, позволяющий обрабатывать символьную информацию. С середины 70-х гг. реализуется идея моделирования конкретных знаний специалистов-экспертов. В США появляются первые экспертные системы. Возникает новая технология искусственного интеллекта, основанная на представлении и использовании знаний. С середины 80-х гг. искусственный интеллект коммерциализируется. Растут капиталовложения в эту отрасль, появляются промышленные экспертные системы, повышается интерес к самообучающимся системам. Базы знаний При изучении интеллектуальных систем необходимо выяснить, что представляют собой знания и в чем их отличие от данных. Понятие знания определяют по-разному, но какого-либо исчерпывающего определения нет. Приведем некоторые из определений: Знания — выявленные закономерности предметной области (принципы, связи, законы), позволяющие решать задачи в этой области. Знания — хорошо структурированные данные, или данные о данных, или метаданные. Знания — совокупность сведений, образующих целостное описание, соответствующее некоторому уровню осведомленности об описываемом вопросе, объекте и т.д. С точки зрения искусственного интеллекта знания определяют как формализованную информацию, на которую ссылаются в процессе логического вывода. Для хранения знаний используют базы знаний. База знаний — основа любой интеллектуальной системы. С точки зрения решения задач в некоторой предметной области знания удобно разделить на две категории — факты и эвристику. Первая категория описывает известные в данной области обстоятельства, знания этой категории иногда называют текстовыми, подчеркивая их достаточное описание в литературе. Вторая категория знаний опирается на практический опыт специалиста-эксперта данной предметной области. Кроме того, знания делят на процедурные и декларативные. Исторически первыми появились процедурные знания, «рассыпанные» в алгоритмах. Они управляли данными. Для их изменения требовалось вносить изменения в программы. С развитием искусственного интеллекта все большая часть знаний формировалась в структурах данных: таблицах, списках, абстрактных типах данных, знания все больше становились декларативными. Декларативные знания — это совокупность сведений о характеристиках свойств конкретных объектов, явлений или процессов, представленных в виде фактов и эвристик. Исторически такие знания накапливались в виде разнообразных справочников, с появлением ЭВМ приобрели форму баз данных. Декларативные знания часто называют просто данными, они хранятся в памяти информационной системы (ИС) так, что имеют непосредственный доступ для использования. Процедурные знания хранятся в памяти ИС в виде описаний процедур, с помощью которых их можно получить. В виде процедурных знаний обычно описывают способы решения задач предметной области, различные инструкции, методики и т.п. Процедурные знания - это методы, алгоритмы, программы решения различных задач в выбранной предметной области, они составляют ядро базы знаний. Процедурные знания образуются в результате осуществления процедур над фактами как исходными данными. Одной из наиболее важных проблем, характерных для систем искусственного интеллекта, является представление знаний. Форма представления знаний существенно влияет на характеристики и свойства системы. Для манипуляции различными знаниями реального мира на компьютере необходимо провести их моделирование. Существует множество моделей представления знаний для различных предметных областей, но большинство из них относятся к следующим классам: логические модели', продукционные модели; семантические сети; фреймовые модели. Традиционно в представлении знаний выделяют формальные логические модели, основанные на классическом исчислении предикатов первого порядка, когда предметная область описывается в виде набора аксиом. Вся информация, необходимая для решения задач, рассматривается как совокупность правил и утверждений, которые представляются как формулы в некоторой логике предикатов. Знания отражают совокупность таких формул, а получение новых знаний сводится к реализации процедур логического вывода. Эта логическая модель применима в основном в исследовательских «идеальных» системах, так как предъявляет высокие требования и ограничения предметной области. В промышленных экспертных системах используются ее различные модификации и расширения. Исследования процессов принятия решений человеком показали, что рассуждая и принимая решение, человек использует продукционные правила (от англ. production — правило вывода, порождающее правило). Продукционная модель, основанная на правилах, позволяет представить знания в виде предложений: ЕСЛИ (список условие), ТО (следует выполнить перечень действий). Условие — это предложение, по которому происходит поиск в базе знаний, а действие есть некоторая операция, выполняемая при успешно осуществленном поиске. Действия могут быть как промежуточными, выступающими далее как условия, так и целевыми, завершающими работу ИС. В продукционной модели база знаний состоит из совокупности правил. Программа, управляющая перебором правил, называется машиной вывода. Механизм выводов связывает знания и создает из их последовательности заключение. Вывод бывает прямой (метод сопоставления, от данных к поиску цели) или обратный (метод генерации гипотезы и ее проверки, от цели — к данным). Пример. Имеется фрагмент базы знаний, состоящий из двух правил: Пр. 1: ЕСЛИ «ведение бизнеса» и «знакомство с Интернет», ТО «электронная коммерция». Пр. 2: ЕСЛИ «владеет компьютером», ТО «знакомство с Интернет».
В систему поступили данные: «ведение бизнеса» и «владеет компьютером». ПРЯМОЙ ВЫВОД: На основе имеющихся данных получить заключение.
1-й проход: Шаг 1. Проверяем Пр. 1, не работает — не хватает данных «знакомство с Интернет». Шаг 2. Проверяем Пр. 2, работает, база дополняется фактом «знакомство с Интернет».
2-й проход Шаг 3. Проверяем Пр. 1, работает, система дает заключение «электронная коммерция».
ОБРАТНЫЙ ВЫВОД: Подтвердить выбранную цель с помощью имеющихся правил и данных.
1-й проход: Шаг 1. Цель — «электронная коммерция»: Проверяем Пр. 1, данных «знакомство с Интернет» нет, они становятся новой целью, и есть правило, где она в правой части. Шаг 2. Цель — «знакомство с Интернет»: Пр. 2 подтверждает цель и активизирует ее.
2-й проход: Шаг 3. Пр. 1 подтверждает искомую цель.
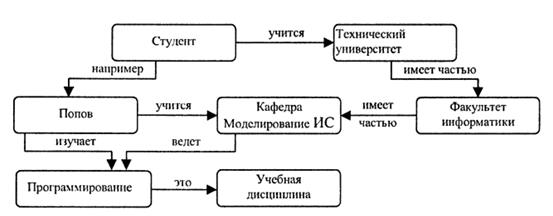
Продукционная модель привлекает разработчиков наглядностью, модульностью, легкостью внесения дополнений и изменений, простотой механизма логического вывода, чаще всего используется в промышленных экспертных системах. Семантика — это наука, исследующая свойства знаков и знаковых систем, их смысловую связь с реальными объектами. Семантическая сеть — это ориентированный граф, вершины которого есть понятия, а дуги — отношения между ними (рис. 6). Это наиболее общая модель знаний, так как в ней имеются средства всех характерных для знаний свойств: внутренней интерпретации, структурированности, семантической метрики и активности.
Рисунок 6. Семантическая сеть
Достоинствами сетевых моделей являются: большие выразительные возможности; наглядность системы знаний, представленной графически; близость структуры сети, представляющей систему знаний, семантической структуре фраз на естественном языке; соответствие современным представлениям об организации долговременной памяти человека. К недостаткам отнесем то, что сетевая модель не содержит ясного представления о структуре предметной области, которая ей соответствует, поэтому ее формирование и модификация затруднительны; сетевые модели представляют собой пассивные структуры, для их обработки используется специальный аппарат формального вывода. Проблема поиска решения в базе знаний типа семантической сети сводится к задаче поиска фрагмента сети, соответствующего некоторой подсети поставленной задачи, что, в свою очередь, говорит еще об одном недостатке модели — сложность поиска вывода на семантических сетях.
Сетевые модели являются наглядным и достаточно универсальным средством представления знаний. Однако их формализация в конкретных моделях представления, использования и модификации знаний представляет достаточно трудоемкий процесс, особенно при наличии множественных отношений между понятиями. Термин фрейм (от англ. frame — каркас, рамка) предложен для обозначения структуры единицы знаний, которую можно описать некоторой совокупностью понятий, для ее пространственного восприятия. Фрейм имеет определенную внутреннюю структуру, состоящую из совокупности элементов, называемых слотами. Каждый слот, в свою очередь, представляется определенной структурой данных, процедурой, или может быть связан с другим фреймом. Фреймовая модель представляет собой систематизированную в виде единой теории технологическую модель памяти человека и его сознания. В отличие от других моделей, во фреймах фиксируется жесткая структура. В общем случае фрейм определяется следующим образом: {ИМЯ ФРЕЙМА: (имя 1-го слота: значение 1-го слота); (имя 2-го слота: значение 2-го слота); (имя N-ro слота: значение N-ro слота)}.
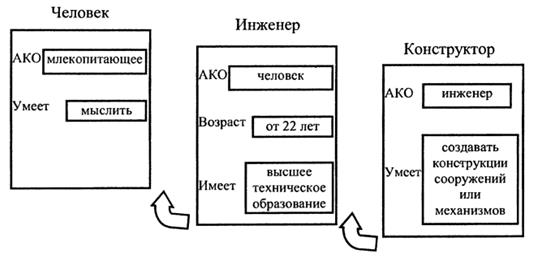
Важным свойством фреймов является наследование свойств, заимствованное из теории семантических сетей. Наследование происходит по АКО-связям (от A Kind Of, что означает «эт.е.»). Слот АКО указывает на фрейм более высокого уровня иерархии, откуда неявно наследуется, т.е. переносятся значения аналогичных слотов. Например, в сети фреймов на рис. 7 «конструктор» наследует свойства фреймов «инженер» и «человек», которые стоят на более высоком уровне иерархии.
Рисунок 7. Сеть фреймов
Модель фрейма достаточно универсальна, позволяет отобразить все многообразие знаний о мире через: • фреймы-структуры, для обозначения объектов и понятий (лекция, конспект, кафедра); • фреймы-роли (студент, преподаватель, декан); • фреймы-сценарии (сдача экзамена, празднование именин, получение стипендии); • фреймы-ситуации (тревога, рабочий режим учебного дня) и др. Основным преимуществом фреймов как модели представления знаний является их способность отражать концептуальную основу организации памяти человека, а также гибкость и наглядность. Обобщая анализ моделей представления знаний, можно сделать следующие выводы: • Нельзя дать универсальных рекомендаций по выбору модели. Этот выбор определяется возможностью и удобством представления исследуемой предметной области с учетом необходимости использования знаний. • Наиболее мощными являются смешанные модели представления знаний.
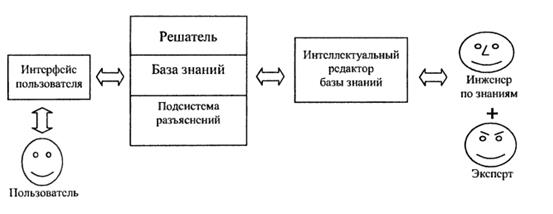
Экспертные системы Предназначены для анализа данных, содержащихся в базах знаний, и выдачи рекомендаций по запросу пользователя. Используются в тех случаях, когда исходные данные хорошо формализуются, но для принятия решения требуются специальные обширные знания. Экспертные системы — это сложные программные комплексы, аккумулирующие знания специалистов в конкретных предметных областях и тиражирующие этот эмпирический опыт для консультаций менее квалифицированных пользователей. Предметные области: медицина, фармакология, химия, геология, экономика, юриспруденция и др., в которых большая часть знаний является личным опытом специалистов высокого уровня (экспертов), нуждаются в экспертных системах. Те области, где большая часть знаний представлена в виде коллективного опыта (например, высшая математика), не нуждаются в них. Экспертная система определяется набором логически взаимосвязанных правил, формирующих знания и опыт специалиста данной предметной области, и механизмом решения, позволяющим распознавать ситуацию, давать рекомендации к действию, ставить диагноз. Современные экспертные системы способны: — по совокупности признаков заболевания установить диагноз, назначить лечение, дозировать медикаменты, выработать программу курса лечения; — выполнять задачи диагностических систем в исследовании явлений и процессов (например, для анализа крови; управления производством; изучения состояния недр земли, нефтяных полей, залежей угля и т.п.); — распознавать речь, на данном этапе в ограниченной области применения; — распознавать человеческие лица, отпечатки пальцев и др. На рис. 8 изображены основные компоненты модели экспертной системы: пользователь (специалист предметной области, для которого данная система предназначена), инженер по знаниям (специалист по искусственному интеллекту — промежуточное звено между экспертом и базой знаний), интерфейс пользователя (приложение, реализующее диалог пользователя и системы), база знаний — ядро экспертной системы, решатель (приложение, моделирующее рассуждения эксперта на основе имеющихся в базе знаний), подсистема разъяснения ( приложение, позволяющее разъяснять на основании чего экспертная система дает рекомендации, делает выводы, какие знания при этом используются ), интеллектуальный редактор базы знаний (приложение, дающее инженеру по знаниям возможность создания базы знаний в диалоговом режиме ).
Рисунок 8. Структура модели экспертной системы.
Характерной особенностью любой экспертной системы является способность к саморазвитию. Исходные данные хранятся в базе знаний в виде фактов, между которыми установлены определенные логические связи. Если при тестировании выявлены некорректные рекомендации или заключения по конкретным вопросам, либо заключение не может быть сформулировано, это означает, или отсутствие важных фактов в ее базе, или нарушения в логической системе связей. В любом случае система сама может сформировать достаточный набор вопросов к эксперту и автоматически повысить свое качество.
Система управления Представляет совокупность взаимосвязанных структурных моделей подсистем, осуществляющих следующие функции: • планирование (стратегическое, тактическое, оперативное); • учет — отображает состояние объекта управления в результате выполнения производственных процессов; • контроль — определяет отклонение учетных данных от плановых целей и нормативов; • оперативное управление — осуществляет регулирование всех процессов с целью исключения возникающих отклонений от плановых и учетных данных; • анализ — определяет тенденцию в работе системы и резервы, которые учитываются при планировании на следующий временной период. Использование моделей в составе информационных систем началось с применения статистических методов и методов финансового анализа, которые реализовывались командами обычных алгоритмических языков. Позже были созданы специальные языки, позволяющие моделировать различные ситуации. Такие языки дают возможность построения моделей определенного типа, обеспечивающих нахождение решения при гибком изменении переменных.
ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ. ОСНОВНЫЕ ПОНЯТИЯ ПРОГРАММИРОВАНИЯ
ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Рассмотренные технические средства ПЭВМ в совокупности являются универсальным инструментом для решения широкого круга задач. Однако эти задачи могут быть решены лишь в том случае, если ПЭВМ «знает» алгоритм их решения. Алгоритм (algorithm) – точное предписание, определяющее процесс преобразования исходных данных в конечный результат. Общими свойствами любого алгоритма являются: – дискретность – возможность разбиения алгоритма на отдельные элементарные действия; – определенность (детерминированность) алгоритма обеспечивает однозначность результата (повторяемость получаемого результата при многократных расчетах с одними и теми же исходными данными) и исключает возможность искажения или двусмысленного толкования предписания; – результативность – обязательное получение за конечное число шагов некоторого результата, а при невозможности получения результата – сигнала о том, что данный алгоритм неприменим для решения поставленной задачи; – массовость – возможность получения результата при различных исходных данных для некоторого класса сходных задач. Программа (program) – данные, их описание и алгоритм, записанный на языке программирования. Программа описывает операци
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 1581; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.28.160 (0.015 с.) |

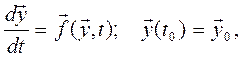
 — n-мерные векторы и
— n-мерные векторы и  — непрерывна.
— непрерывна. .
.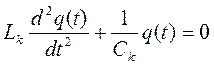 .
.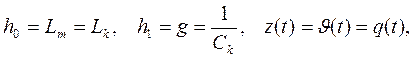 получим уравнение, описывающее состояние во времени обеих систем
получим уравнение, описывающее состояние во времени обеих систем