
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Практические занятия № 23-24Содержание книги Поиск на нашем сайте
Тема: «Нормальное распределение»
1.Случайная величина Х подчинена нормальному закону распределения с математическим ожиданием М(Х) = 2 и средним квадратичным отклонением σ(Х)=3. Запишите плотность вероятности Х. 2. Случайная величина Х подчинена нормальному закону распределения с математическим ожиданием М(Х) = 2 и дисперсией 3. Х- нормальная случайная величина, плотность вероятности которой определяется формулой Задача 4. Случайная величина Х подчинена нормальному закону распределения с математическим ожиданием М(Х) =10 и средним квадратичным отклонением σ(Х)=2. Найти вероятность попадания Х в интервал [12; 14]. Решение. Воспользуемся формулой:
Имеем:
5.Случайная величина Х подчинена нормальному закону распределения с математическим ожиданием М(Х) =20 и средним квадратичным отклонением σ(Х)=5. Найти вероятность попадания Х в интервал [15; 25]. Ответ. 0,6826. 6. Случайная величина Х подчинена нормальному закону распределения с математическим ожиданием М(Х) =2 и средним квадратичным отклонением σ(Х)=1. Найти вероятность следующих неравенств: а) 1 < Х < 3; б) 0 < Х < 2; в) 7. Автомат штампует детали. Контролируется длина детали Х, которая имеет нормальное распределение с математическим ожиданием М(Х)=50мм (проектная длина) и средним квадратичным отклонением 8. Случайные ошибки измерения Х подчинены нормальному распределению с а =0. Найти среднее квадратичное отклонение Х, если известно, что вероятность события 9. Случайная величина Х подчинена нормальному распределению с а =0. Найти среднее квадратичное отклонение Х, если известно, что вероятность события
Задача 10. Производится взвешивание некоторого вещества без систематических ошибок. Случайные ошибки измерения подчинены нормальному распределению с а =0 и σ =20г. Найти вероятность того, что взвешивание будет произведено с ошибкой, не превышающей 10г.
Решение. Воспользуемся формулой:
11. Случайная величина Х подчинена нормальному закону распределения с математическим ожиданием М(Х) =10 и средним квадратичным отклонением σ(Х)=5. Найти интервал, симметричный относительно математического ожидания, в котором Х будет заключена с вероятностью а) 0,9974; б) 0,5. Ответ. а) (-5; 25); б) (6,6; 13,4) 12. Случайные ошибки измерения подчинены нормальному распределению с а = 0 и σ = 20. Найти вероятность того, что из трех независимых измерений хотя бы в одном измерении ошибка по абсолютной величине не превзойдет 4. Ответ. 0,404. 13. Случайная величина Х подчинена нормальному закону распределения с математическим ожиданием М(Х) =10 и средним квадратичным отклонением σ(Х)=3. Пользуясь правилом «3σ» найти интервал, симметричный относительно математического ожидания, куда Х попадет с вероятностью 0,9973. Ответ. (1; 19). 14. Автомат изготавливает диски проектным диаметром 2,5см. Случайные ошибки (точность автомата) подчинены нормальному распределению с М(Х) =0 и D(Х)=0,0001. Пользуясь правилом «3σ» найти интервал, симметричный относительно математического ожидания, куда Х попадет с вероятностью 0,9973. Ответ. (2,47; 2,53). 15. Станок-автомат штампует плитки. Контролируется толщина плитки Х. Проектная толщина плитки равна 5мм. Фактически толщина плитки колеблется от 2,3 до7,7мм. Плитка признается стандартной, если ее толщина от 4 до 6мм. Сколько процентов стандартной плитки изготовляет автомат? Ответ. 73,3%.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 25 Тема 1.: «Гистограмма и полигон»
Задача 1. Для заданных выборок найти: а) распределение относительно частот; б) эмпирическую функцию распределения; в) построить полигон частот и полигон относительных частот 1)
2)
3)
4)
Задача 2. Для следующих выборок найти: а) распределение относительно частот; б) функцию распределения; в) построить гистограмму частот; г) построить полигон частот 1)
2)
3)
4)
Тема 2.: «Точечные оценки статического распределения»
По данным выборкам найти выборочное среднее, выборочную дисперсию, исправленную дисперсию. Задача 1. Приводятся результаты наблюдений за числом неправильных соединений на телефонной станции за каждую минуту в течение часа; хi – количество неправильных соединений, ni – число минутных интервалов
Задача 2. Приводятся ошибки 40 измерений некоторой физической величины ni – количество ошибок, лежащих в интервале (xi,xi+1)
Задача 3. Приводятся данные ежедневных измерений температуры в течение месяца ti, ti+1 – температурный интервал, ni – число наблюдений
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 438; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.107.101 (0.009 с.) |

 . Запишите плотность вероятности Х.
. Запишите плотность вероятности Х.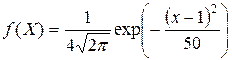 . Найти математическое ожидание и дисперсию Х.
. Найти математическое ожидание и дисперсию Х.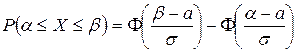 .
.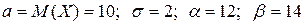 . Тогда
. Тогда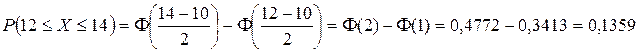 Ответ. 0,1359.
Ответ. 0,1359. ; г) X < 3; д) X > 0. Ответ. а) 0,6826; б) 0,4772; в) 0,84129; г) 0,8413; д) 0,9772.
; г) X < 3; д) X > 0. Ответ. а) 0,6826; б) 0,4772; в) 0,84129; г) 0,8413; д) 0,9772. . Деталь считается годной, если ее отклонение от проектной величины не превышает 10мм. Сколько процентов годных деталей изготовляет автомат? Ответ. 90,3%.
. Деталь считается годной, если ее отклонение от проектной величины не превышает 10мм. Сколько процентов годных деталей изготовляет автомат? Ответ. 90,3%.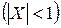 равна 0,6626. Ответ. ≈1,04.
равна 0,6626. Ответ. ≈1,04.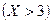 равна 0,0288. Ответ. ≈1,58.
равна 0,0288. Ответ. ≈1,58. . Имеем:
. Имеем: 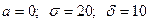 . Тогда
. Тогда 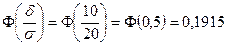 . Искомая вероятность равна 2∙0,1915=0,383. Ответ. 0,383.
. Искомая вероятность равна 2∙0,1915=0,383. Ответ. 0,383.


