
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Практические занятия №11 - 12Содержание книги Поиск на нашем сайте
Тема: «Ряды Фурье»
Задача 1. Разложить в ряд Фурье периодическую функцию Решение. Данная функция четная. Все коэффициенты
(Здесь дважды применена формула интегрирования по частям). Вычислим
Следовательно,
Задание. 1.Разложить в ряд Фурье периодическую функцию 2.Разложить в ряд Фурье периодическую функцию 3. Разложить в ряд Фурье периодическую функцию 4. Разложить в ряд Фурье функцию периода
Задача 2. Разложить в ряд Фурье функцию, заданную формулой
Решение. Продолжим функцию
Таким образом,
Замечание. Можно было продолжить исходную функцию нечетным образом. 5. Разложить в ряд Фурье по косинусам функцию Ответ. 6. Разложить в ряд Фурье по синусам функцию Ответ. 6. Разложить в ряд Фурье по косинусам функцию Ответ.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 13 Тема: «Элементы комбинаторики»
Задача 1. Вычислить а) Решение. а) Воспользуемся формулой
б) Воспользуемся формулой
в) Воспользуемся формулой
Задание. 1. Вычислить: 1) 3!; 2) 5!; 3) 6!; 4) 7!. Ответ. 1) 6; 2) 120; 3) 720; 4) 5040. 2. Вычислить: 1) 3. Вычислить: 1) Ответ. 1) 4; 2) 6; 3) 4; 4) 1; 5) 28; 6) 10. 4. Имеется 5 видов конвертов без марок и 4 вида марок одного достоинства. Сколькими способами можно выбрать конверт с маркой для отправки письма? Ответ. 20. 5. В магазине имеется 5 видов рубашек, 3 вида брюк и 6 видов галстуков. Сколькими способами можно подобрать набор брюки – рубашка – галстук? Ответ. 90. 6. Группа студентов из 30 человек решила обменяться фотокарточками. Сколько всего фотокарточек понадобилось для этого? Ответ. 870. 7. Сколько вариантов хоккейной команды можно составить из 9 нападающих, 5 защитников и 3 вратарей, если в состав команды входят 3 нападающих, 2 защитника и 1 вратарь? Ответ. 2520. 8. На плоскости имеется 8 точек, из которых 3 лежат на одной прямой. Сколько различных прямых линий можно провести, если брать различные пары из имеющихся точек? Ответ. 26. 9. Кодовый замок открывается набором из четырех цифр. Сколько может быть различных комбинаций набора? Ответ.
10. Сколько существует шестизначных чисел, все цифры которых различны? Ответ. 136080. 11. Сколько существует «зеркальных» шестизначных чисел, которые одинаково читаются слева направо и справа налево? Ответ. 648. 12. Группа из десяти мальчиков и десяти девочек размещается в ряд на скамейке. Сколько существует вариантов размещения при которых: а) никакие два мальчика не сидят рядом? б) все мальчики сидят одной группой? в) Коля сидит рядом с Олей? Ответ. а) 2∙10!∙10! б) 11 ∙10! ∙10! в) 2 ∙19 ∙18! 13. В гостиницу прибыло семь командированных мужчин. Имеются свободные номера: одноместный, двуместный и четырехместный. а) Сколько существует вариантов размещения прибывших?б) Сколько вариантов того, что Иванов и Петров попадут в один номер? Ответ. а) 105; б) 35. 14. На первую горизонталь шахматной доски (8 клеток) расставляются пять фигур. Сколько существует различных вариантов расстановки, если эти фигуры: а) король, ферзь, конь, слон, ладья? б) король, ферзь, конь и два слона? в) король, два коня и два слона? г) пять пешек? Ответ. а) 6720. б) 3360. в) 1680. г) 56. 15. Сколько существует шестизначных чисел, в записи которых есть хоть одна четная цифра? Ответ. 884375. 16. Сколько существует семизначных чисел, в записи которых есть хоть одна единица? Ответ. 17.Из колоды в 52 карты (4 масти по 13 карт) вынимаются четыре карты. а) Сколько существует вариантов выбора, при которых среди выбранных карт будет хоть одна карта «красной» масти? б) Сколько существует вариантов выбора, при которых среди выбранных карт будет хоть один туз? Ответ. а)
|
|||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 437; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.145.41 (0.006 с.) |

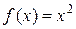 при
при  .
. , а коэффициенты
, а коэффициенты 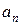 вычисляются при
вычисляются при 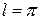 .
.

 .
. при
при  . Ответ.
. Ответ. 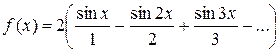 .
. при
при  .
. в интервале
в интервале 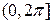 . Ответ.
. Ответ. 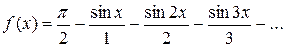 .
. , заданную формулой
, заданную формулой Ответ.
Ответ. 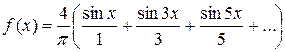 .
.
 на отрезок
на отрезок 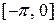 четным образом, затем периодически продолжим ее с периодом
четным образом, затем периодически продолжим ее с периодом 
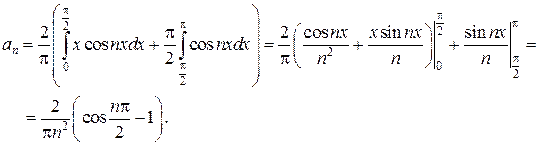
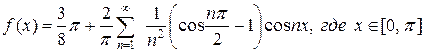 .
. ,
,  .
.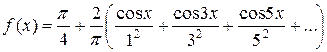 , где
, где 
 , где
, где  .
.
 .
.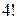 б)
б) 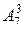 в)
в) 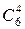
 . Тогда
. Тогда .
. . Тогда
. Тогда .
. . Тогда
. Тогда .
. ; 2)
; 2)  ; 3)
; 3)  . Ответ. 1) 60; 2) 10; 3) 30.
. Ответ. 1) 60; 2) 10; 3) 30. ; 2)
; 2)  ; 3)
; 3) 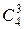 ; 4)
; 4)  ; 5)
; 5)  ; 6)
; 6)  .
. .
. .
. . б)
. б)  .
.


