
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Практические занятия № 5 - 6.
Тема: «Достаточные признаки сходимости положительных числовых рядов» Задача 1. Исследовать по признаку Даламбера сходимость ряда Решение.
Так как Задание. Исследовать по признаку Даламбера сходимость ряда. 1. 3. 5.
Задача 2. Исследовать по признаку Коши сходимость ряда Решение. Т. к.
Задание. Исследовать по признаку Коши сходимость ряда 1. 3. 5. 6. При каких значениях с сходится ряд
Задача 3. Исследовать по интегральному признаку сходимость ряда
Решение. Рассмотрим функцию
Этот несобственный интеграл расходится. Следовательно, согласно интегральному признаку и данный ряд также расходится.
Задание. Исследовать по интегральному признаку сходимость ряда. 1. 3. 5. Задача 4. Исследовать по признаку сравнения сходимость ряда Решение. Сравним данный ряд с гармоническим рядом Задание. Исследовать по признаку сравнения сходимость ряда 1. 3. 5.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 7 Тема: «Абсолютная и условная сходимость числовых рядов»
Задача 1. Исследовать сходимость ряда (определить, является ли он абсолютно сходящимся, условно сходящимся, расходящимся) Решение. Для этого знакочередующегося ряда выполнены условия признака Лейбница: 1) Следовательно, указанный ряд сходится. Однако ряд, составленный из модулей членов данного ряда, т.е. ряд
Задание. Исследовать сходимость ряда.
1. 2. 3. 4. 5. 6. 7. 8. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 8 Тема: «Степенные ряды» Задача 1. Найти область сходимости ряда Решение. Имеем
Следовательно ряд сходится при любом значении Задача 2. Найти область сходимости ряда Решение. Имеем
Исследуем поведение ряда на концах интервала сходимости При Следовательно, областью сходимости исходного ряда является полуотрезок Задача 3. Найти область сходимости cтепенного ряда Решение. Имеем
Следовательно, ряд сходится при При
который сходится по признаку Лейбница. При
который расходится (гармонический ряд). Следовательно, областью сходимости исходного ряда является полу-отрезок
Задание. Найти область сходимости ряда. 1. 3. 5. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 9 Тема: «Разложение функций в степенные ряды»
Задача 1. Разложить в ряд Маклорена функцию Решение. Найдем значения функции и ее производных при
………………………………..
Получим:
Задача 2. Выписать ряд Маклорена функции Решение. В разложении
заменим
Задача 3. Разложить в ряд Маклорена функцию Решение. Воспользуемся формулой
Так как
то заменив
где
Задание. Разложить в ряд Маклорена. 1. 2. 3. Разложить Ответ. 4.Разложить Ответ. 5. Выписать ряд Маклорена для функции Ответ. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 10 Тема: «Некоторые приложения степенных рядов»
Задача 1. Вычислить Решение. Преобразуем корень
Полагаем в разложении функции
Здесь частичная сумма
Задание. 1. Вычислить 2. Вычислить
3. Вычислить Задача 2. Вычислить интеграл Решение.
4. Вычислить интеграл Ответ. 5. Вычислить интеграл Ответ.
|
||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 682; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.147.4 (0.031 с.) |
 .
. ; находим
; находим
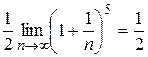 .
.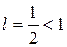 , то данный ряд по признаку Даламбера сходится.
, то данный ряд по признаку Даламбера сходится. . Ответ. Расходится. 2.
. Ответ. Расходится. 2.  . Ответ. Расходится.
. Ответ. Расходится. . Ответ. Сходится. 4.
. Ответ. Сходится. 4.  . Ответ. Расходится.
. Ответ. Расходится. . Ответ. Сходится. 6.
. Ответ. Сходится. 6.  . Ответ. Расходится.
. Ответ. Расходится. .
. находим
находим  .
.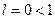 , то данный ряд по признаку Коши сходится.
, то данный ряд по признаку Коши сходится. . Ответ. Сходится. 2.
. Ответ. Сходится. 2.  . Ответ. Расходится.
. Ответ. Расходится. . Ответ. Сходится. 4.
. Ответ. Сходится. 4. 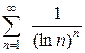 . Ответ. Сходится.
. Ответ. Сходится. . Ответ. Расходится.
. Ответ. Расходится.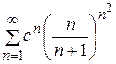 ? Ответ. При
? Ответ. При  .
. .
. . Найдем несобственный интеграл
. Найдем несобственный интеграл
 .
. . Ответ. Сходится. 2.
. Ответ. Сходится. 2.  . Ответ. Расходится.
. Ответ. Расходится. . Ответ. Сходится. 4.
. Ответ. Сходится. 4.  . Ответ. Сходится.
. Ответ. Сходится. . Ответ. Сходится.
. Ответ. Сходится. .
. . Каждый член
. Каждый член  данного ряда, начиная со второго, больше соответствующего члена
данного ряда, начиная со второго, больше соответствующего члена  гармонического ряда:
гармонического ряда:  , и т.к. гармонический ряд расходится, то согласно признаку сравнения, данный ряд также расходится.
, и т.к. гармонический ряд расходится, то согласно признаку сравнения, данный ряд также расходится.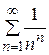 . Ответ. Сходится. 2.
. Ответ. Сходится. 2.  . Ответ. Сходится.
. Ответ. Сходится. . Ответ. Сходится. 4.
. Ответ. Сходится. 4.  . Ответ. Расходится.
. Ответ. Расходится. . Ответ. Расходится.
. Ответ. Расходится. .
. 2)
2)  .
. расходится (гармонический ряд). Значит исходный ряд условно сходящийся.
расходится (гармонический ряд). Значит исходный ряд условно сходящийся. . Ответ. Абсолютно сходится.
. Ответ. Абсолютно сходится.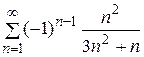 . Ответ. Расходится.
. Ответ. Расходится.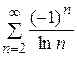 . Ответ. Условно сходится.
. Ответ. Условно сходится. . Ответ. Абсолютно сходится.
. Ответ. Абсолютно сходится.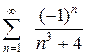 . Ответ. Абсолютно сходится.
. Ответ. Абсолютно сходится. . Ответ. Абсолютно сходится.
. Ответ. Абсолютно сходится.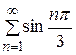 . Ответ. Расходится.
. Ответ. Расходится. . Ответ. Расходится.
. Ответ. Расходится. .
.
 .
. .
. .
. .
.  .
. .
. имеем ряд
имеем ряд  , который расходится (гармонический ряд). При
, который расходится (гармонический ряд). При 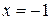 имеем ряд
имеем ряд 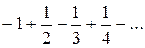 , который сходится по признаку Лейбница.
, который сходится по признаку Лейбница. .
. .
. .
.  .
. , т.е. при
, т.е. при 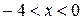 .
.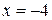 имеем ряд
имеем ряд ,
, имеем ряд
имеем ряд ,
, .
. . Ответ. (-7, 7). 2.
. Ответ. (-7, 7). 2.  . Ответ. [1, 3].
. Ответ. [1, 3]. . Ответ. [2, 8). 4.
. Ответ. [2, 8). 4. 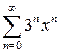 . Ответ.
. Ответ. 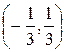 .
. . Ответ.
. Ответ.  .
. .
.




 .
. .
.
 ; получим:
; получим:
 .
.
 ,
, , получим:
, получим: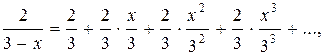
 , т.е.
, т.е.  .
. . Ответ.
. Ответ. 
 . Ответ.
. Ответ.  .
. в ряд по степеням
в ряд по степеням 
 в ряд по степеням
в ряд по степеням  .
. .
. .
. .
. с точностью 0,0001.
с точностью 0,0001. .
. и умножая его на 3 получим
и умножая его на 3 получим
 .
. обеспечивает заданную точность, т.к.
обеспечивает заданную точность, т.к.
 с точностью 0,0001. Ответ.
с точностью 0,0001. Ответ.  .
. с точностью до 0,001. Ответ.
с точностью до 0,001. Ответ.  .
. с точностью до 0,0001. Ответ.
с точностью до 0,0001. Ответ.  .
. с точностью до 0,001.
с точностью до 0,001.

 с точностью до 0,0001.
с точностью до 0,0001.
 с точностью до 0,001.
с точностью до 0,001.



