
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Практические занятия № 18-19Содержание книги Поиск на нашем сайте
Тема 1: «Повторение испытаний. Схема Бернулли»
Задача 1. Вероятность перерасхода воды на предприятии в течение одного дня равна 0,1. Каковы вероятности того, что в течение пятидневной рабочей недели перерасход воды произойдет от одного до пяти раз? Решение. Воспользуемся формулой Бернулли:
Задание 1. Два равносильных противника играют в шахматы без ничьих. Что вероятнее: а) выиграть две партии из четырех или три партии из шести? б) выиграть не менее двух партий из трех или не менее трех партий из пяти? Ответ. а) две партии из четырех; б) одинаковая вероятность. 2. Монету бросают пять раз. Найти вероятность того, что «герб» выпадет:а) менее двух раз; б) не менее двух раз. Ответ. а) 3. Какова вероятность выпадения хотя бы двух шестерок при трех бросках игральной кости? Ответ. 4. Вероятность попадания в цель при одном выстреле равна 0,25. Было произведено пять выстрелов. Какова вероятность а) не менее трех попаданий? б) хотя бы одного попадания? Ответ. а) Задача 2. Вероятность попадания в цель при одном выстреле равна 0,4. Сколько выстрелов должен сделать стрелок, чтобы с вероятностью не менее 0,9 он хотя бы один раз попал в цель? Решение. Вероятность того, что при n выстрелах не будет ни одного попадания равна 5. Сколько раз надо бросить игральную кость, чтобы вероятность выпадения хотя бы одной шестерки была больше 0,8? Ответ. не менее 9. 6. В лотерее выигрывает каждый пятый билет. Сколько билетов надо приобрести, чтобы вероятность того, что хотя бы один билет выиграет, была больше 0,7? Ответ. Не менее 6. 7. Партия изделий содержит 1% брака. Каков должен быть объем контрольной выборки, чтобы вероятность обнаружить в ней хотя бы одно бракованное изделие была не меньше 0,95? Ответ. Не менее 299 изделий.
Задача 3. Товаровед осматривает 24 образца товаров. Вероятность того, что каждый из образцов будет признан годным к продаже, равна 0,6. Найти наивероятнейшее число образцов, которые товаровед признает годными к продаже. Решение. Наивероятнейшее число
8. Вероятность попадания в цель при одном выстреле равна 0,8. произведено 15 выстрелов. Найти наивероятнейшее число попаданий. Ответ. 12.
Тема 2: «Локальная и интегральная теоремы Лапласа»
Задача 1. Вероятность брака при штамповке деталей равна 0,05. Найти вероятность того, что в партии из 10000 деталей бракованными окажутся а) ровно 500 деталей; б) ровно 530 деталей. Решение. а) Имеем Воспользуемся формулой локальной теоремы Лапласа
Тогда
Для случая а) х= 0. По таблице находим Тогда
1. Вероятность рождения мальчика равна 0,51. Найти вероятность того, что среди 100 новорожденных будет ровно а) 50 мальчиков б) 51 мальчик. Ответ. а) 0,0782, б) 0,07978. 2. Посеяно 10000 семян. Вероятность того, что семя не прорастет, равна 0,0003. Какова вероятность того, что все семена прорастут? Ответ. 0,0516. 3. Вероятность выхода из строя одного элемента в течение года равна 0,2. Какова вероятность того, что из 100 элементов в течение года выйдут из строя ровно 15? Ответ. 0,04565. 4. Вероятность прерывания телефонного соединения равна 0,03. Какова вероятность того, что среди 100 телефонных соединений будет ровно одно прерывание? Ответ. 0,118.
Задача 2. Телефонная станция обслуживает 600 абонентов. Вероятность любого абонента позвонить в течение часа равна 0,05. Какова вероятность того, что в течение часа позвонят от 5 до 45 человек? Решение. Искомую вероятность найдем с помощью интегральной теоремы Лапласа:
где а значение функции Φ находится по специальной таблице. Имеем: n = 600, p = 0,05, q = 1- p =0,95, Вычислим:
По таблице находим: Тогда
5. Газета содержит 20000 букв. Каждая буква может быть неправильно напечатана с вероятностью 0, 004. Какова вероятность того, что в газете будет не менее двух опечаток? Ответ. 0, 9830.
6. При штамповке деталей вероятность брака составляет 1%. Какова вероятность того, что среди 10000 случайно отобранных деталей не более 110 окажутся бракованными? Ответ. 0,8413. 7. Завод отправил в магазин 5000 лампочек. Вероятность того, что лампочка при транспортировке разобьется, равна 0,0002. Найдите вероятность того, что в магазин привезут не более трех разбитых лампочек. Ответ. 0,8185. 8. В страховой компании застраховано 10000 автомобилей. Страховой взнос в год составляет 30 у.е., а в случае аварии компания выплачивает пострадавшему 3000у.е. Вероятность аварии для одного автомобиля в течение года составляет0,006. Найти вероятность следующих событий: А – в течение года компания потерпит убыток; В – прибыль компании за год превысит 60000у.е.; С - прибыль компании за год превысит 120000у.е.; D - прибыль компании за год превысит 180000у.е. Ответ. Р(А)=0; Р(В)=0,9952; Р(С)=0,5; Р(D)=0,0048.
Тема 3: «Отклонение относительной частоты от теоретической вероятности»
При решении задач по этой теме используется формула: 1. Вероятность появления события в каждом из 900 испытаний равна 0,5. Найти вероятность того, что относительная частота отклонится от вероятности по абсолютной величине не более чем на 0,02. Ответ. 0,7698. 2. Вероятность появления события в каждом из 10000 испытаний равна 0,75. найти вероятность того, что относительная частота появления события отклонится от вероятности по абсолютной величине не более чем на 0,04. Ответ. 0,979.
Задача 1. Вероятность появления события в опыте равна 0,2. Найти число испытаний n, при котором с вероятностью примерно 0,99 можно ожидать, что отклонение относительной частоты от теоретической вероятности по абсолютной величине не превзойдет 0,04. Решение. Имеем: Ответ. 666.
3. В урне содержатся белые и черные шары в соотношении 4:1 (белых к черным). Из урны наудачу вынимается шар, регистрируется его цвет, после чего шар возвращается обратно. Чему равно минимальное число опытов, при котором с вероятностью 0,95 можно ожидать, что относительная частота появления белого шара отклонится от вероятности по абсолютной величине не более чем на 0,01. Ответ. 6147. 4. Вероятность попадания в мишень при одном выстреле равна 0,7. Сколько выстрелов надо сделать, чтобы отклонение относительной частоты попаданий от вероятности не превышало бы 0,01 с вероятностью а) 0,96? б) 0,9? Ответ. а) 8826; б) 5718. 5. Вероятность появления события в каждом из 400 независимых испытаний равна 0,8. Найти такое положительное число ε, чтобы с вероятностью 0,99 отклонение относительной частоты от вероятности не превысило бы ε. Ответ. 0,05. 6.Вероятность появления события в каждом из 10000 независимых испытаний равна 0,75. Найти такое положительное число ε, чтобы с вероятностью 0,98 отклонение относительной частоты от вероятности не превысило бы ε. Ответ. 0,01.
Задача 2. Небольшой городок ежедневно посещает 100 туристов, которые независимо друг от друга идут обедать в один из двух ресторанов. Владелец одного из ресторанов хочет, чтобы с вероятностью, близкой к 0,99 все клиенты, пришедшие к нему, могли бы пообедать без очереди. Сколько мест должен он держать в ресторане? Решение. Определим границы числа посетителей ресторана с точностью 0,99. Имеем:
7. ОТК проверяет на брак 475 деталей. Вероятность того, что деталь бракованная, равна 0,05. Найти с вероятностью 0,95 границы, в которых будет заключено число бракованных деталей. Ответ. От 14 до 34. 8. Игральную кость бросают 80 раз. Найти с вероятностью границы, в которых будет заключено число выпадений шести очков а) с вероятностью 0,99; б0 с вероятностью0,8. Ответ. а) от 4 до 22; б) от 9 до 12. 9. При штамповке деталей вероятность брака составляет1%. Найти с вероятностью 0,9 границы, в которых будет заключено число бракованных деталей в партии из 1000 деталей. Ответ. От 9 до 15.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 20 Тема: «Дискретные СВ и их характеристики» Задача 1. Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента равна 0,1. Случайная величина Х – число отказавших элементов. Составить закон распределения СВ Х и найти математическое ожидание и дисперсию Х. Решение. Очевидно, что СВ Х может принимать значения от 0 до 3. Для нахождения вероятности того, что Х примет значение k, воспользуемся формулой Бернулли:
Составим таблицу:
Проверим выполнение условия Вычислим математическое ожидание Х, воспользовавшись формулой
Для вычисления дисперсии воспользуемся формулой:
Тогда
1. В ящике 4 годных и 2 бракованных детали. Наудачу из ящика вынимают две детали. СВ Х – число годных деталей среди вынутых. Найти закон распределения СВ Х. 2. В ящике 4 годных и 2 бракованных детали. Детали достаются по одной, пока не будут отобраны две годных детали. СВ Х – число вынутых деталей. Найти закон распределения СВ Х. 3. Стрелку выдано три патрона. Стрелок стреляет в цель до первого попадания или пока не кончатся патроны. Вероятность попадания в цель при одном выстреле равна 0,8. СВ Х – число выстрелов. Найти закон распределения СВ Х. 4. В партии деталей 10% нестандартных. Наудачу отобраны 4 детали. СВ Х – число нестандартных деталей среди отобранных. Найти закон распределения СВ Х и его математическое ожидание.
5. Дискретная СВ задана законом распределения
Известно, что математическое ожидание этой СВ равно 8. Найти х3 и р3 Ответ. х3=21, р3=0,2. 6. Дискретная СВ задана таблицей распределения
Написать закон распределения СВ 7. Найти математическое ожидание и дисперсию СВ Х, где Х – число выпавших на игральной кости очков при одном броске. Ответ. 8. Найти математическое ожидание и дисперсию СВ Х, заданной таблицей распределения
Ответ. 9. По заданной таблице распределения найти дисперсию СВ Х
Ответ.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 21 Тема: «Непрерывные СВ и их характеристики»
Задача 1. Случайная величина Х задана плотностью распределения
Найти 1) коэффициент a; 2) функцию распределения Решение. 1) Для нахождения коэффициента а используем формулу
Приравняв вычисленное значение к 1, получим 2) Для вычисления функции распределения воспользуемся формулой
Тогда при
при
Окончательно, 3) Математическое ожидание М(X) найдем по формуле
Тогда Дисперсию
Тогда
Откуда 4) Для нахождения вероятности попадания СВ Х в интервал [0, 2] воспользуемся формулой Тогда Ответ. 1) 3) Задание. 1. Дано: 2.Дано: Ответ. 3.По заданной функции распределения Найти плотность распределения 4.По заданной функции распределения Найти плотность распределения 5.Найти коэффициент c, если 6. Дано 7. Дано: 8. Дано: 9. По заданной плотности вероятности Найти математическое ожидание М(X). Ответ. 10. Дано: 11. По заданной функции распределения 12. По заданной функции распределения Найти дисперсию 13. По заданной плотности вероятности 14. СВ х задана плотностью вероятности Найти дисперсию СВ
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 22 Тема: «Основные распределения СВ»
1. Две игральные кости бросаются до первого выпадения шести очков хотя бы на одной кости. Найти вероятность того, что первый раз шесть очков выпадет при k –ом броске 2. Проводятся испытания по схеме Бернулли с вероятностью успеха в одном испытании p. Вычислить вероятность того, что все k успехов в n испытаниях появятся подряд. Ответ. 3. Вероятность отказа каждого прибора в испытаниях не зависит от отказов остальных приборов и равна 0,2. Испытываются серии по девять приборов. Найти наиболее вероятное число отказавших приборов в серии. Ответ. 2. 4. Устройство состоит из 1000 элементов, работающих независимо друг от друга. Вероятность отказа одного элемента в течение времени Т равна 0,002. Найти вероятность того, что за время Т откажут ровно три элемента.
Ответ. 5. Среднее число вызовов, поступающих на АТС за минуту равно 120. Найти вероятности следующих событий: А – за две секунды не поступило не одного вызова; В - за две секунды поступило менее двух вызовов; С – за одну секунду поступило ровно три вызова; D – за три секунды поступило более трех вызовов. Ответ. 6.Найти среднее число λ бракованных изделий в партии, если вероятность того, что в партии есть хоть одно бракованное изделие, равна 0,95. Ответ. 3. 7. Ошибка округления в экспериментах по измерению подчинена равномерному распределению. Цена деления шкалы измерительного прибора равна 0,2. Найти: а) среднюю ошибку округления; б) вероятность того, что ошибка округления при одном измерении будет меньше 0,04. Ответ. а) 0,1; б) 0,4. 8.Ребро куба Х измерено приблизительно: Ответ. 9.Диаметр диска d измерен приближенно: 10.Время ожидания у бензоколонки АЗС подчинено показательному распределению со средним временем ожидания 6 минут. Найти вероятности событий: А – время ожидания не менее трех и не более шести минут; В – время ожидания более двенадцати минут. Ответ. 11.Время безотказной работы прибора распределено по показательному закону с параметром λ. Вычислить вероятность того, что прибор не выйдет из строя в течение времени
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 1992; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.92.6 (0.009 с.) |

 . Тогда вероятность того, что перерасход воды произойдет только один раз равна
. Тогда вероятность того, что перерасход воды произойдет только один раз равна  , вероятность того, что перерасход произойдет дважды, равна
, вероятность того, что перерасход произойдет дважды, равна  . Вероятность того, что перерасход воды произойдет три раза, равна
. Вероятность того, что перерасход воды произойдет три раза, равна  ; четыре раза -
; четыре раза - 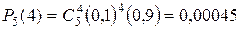 . Вероятность того, что перерасход произойдет пять раз равна
. Вероятность того, что перерасход произойдет пять раз равна 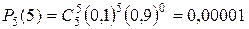 . Наконец вероятность того, что перерасхода воды не произойдет, равна
. Наконец вероятность того, что перерасхода воды не произойдет, равна  .
.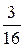 б)
б) 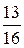 .
. .
. б)
б) 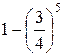 .
. . Вероятность того, что будет хоть одно попадание равна
. Вероятность того, что будет хоть одно попадание равна 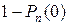 . Таким образом решение задачи сводится к решению неравенства
. Таким образом решение задачи сводится к решению неравенства  ;
;  . Имеем:
. Имеем:  ;
;  . Следовательно, нужно сделать не менее пяти выстрелов.
. Следовательно, нужно сделать не менее пяти выстрелов. наступления события в независимых испытаниях определяется двойным неравенством
наступления события в независимых испытаниях определяется двойным неравенством  . По условию
. По условию  . Тогда
. Тогда 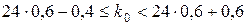 или
или  . Так как
. Так как 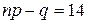 - целое число, то наивероятнейших чисел два: 14 и 15.
- целое число, то наивероятнейших чисел два: 14 и 15. . Для случая а) k =500; для случая б) k =530.
. Для случая а) k =500; для случая б) k =530. где
где 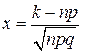 .
.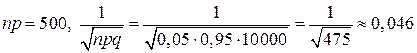 .
. .
. . Ответ. а) 0,018; б) 0,007.
. Ответ. а) 0,018; б) 0,007. ,
, ,
,  ,
, .
. ,
,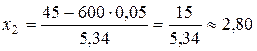 ,
,  .
. ,
, 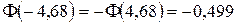 .
. Ответ. 0,996.
Ответ. 0,996.
 . Так как по формуле
. Так как по формуле  , то
, то  , откуда
, откуда  . По таблице находим:
. По таблице находим:  , откуда
, откуда  ,
,  .
. . Воспользуемся формулой отклонения относительной частоты от вероятности:
. Воспользуемся формулой отклонения относительной частоты от вероятности:  . Тогда
. Тогда  ;
;  ;
;  , откуда
, откуда  . Обратимся к левой части формулы:
. Обратимся к левой части формулы:  , где m – число происшедших событий, в данном случае число посетителей ресторана. Отсюда
, где m – число происшедших событий, в данном случае число посетителей ресторана. Отсюда  ;
;  ;
;  ;
; 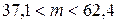 . Следовательно, с вероятностью 0,99 число посетителей ресторана лежит между 37 и 63. Чтобы все посетители могли пообедать без очереди, в ресторане должно быть 63 места. Ответ. 63.
. Следовательно, с вероятностью 0,99 число посетителей ресторана лежит между 37 и 63. Чтобы все посетители могли пообедать без очереди, в ресторане должно быть 63 места. Ответ. 63. . Имеем:
. Имеем: 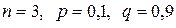 . Тогда
. Тогда ;
;
 ;
; .
. . Действительно 0,729 + 0,243 + 0,027 + 0,001 = 1. Следовательно получен закон распределения СВ Х.
. Действительно 0,729 + 0,243 + 0,027 + 0,001 = 1. Следовательно получен закон распределения СВ Х. . Тогда
. Тогда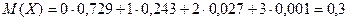 .
. .
.
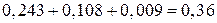 .
. . Ответ.
. Ответ.  .
.

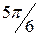
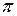



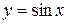 .
.
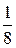


 .
.

 .
.
 ; 3) математическое ожидание и дисперсию Х; 4) вероятность попадания Х в интервал [0, 2].
; 3) математическое ожидание и дисперсию Х; 4) вероятность попадания Х в интервал [0, 2]. . Тогда
. Тогда 
 .
. , откуда
, откуда  .
. .
. имеем
имеем  ; при
; при  имеем
имеем .
. имеем
имеем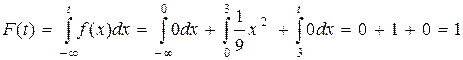 .
.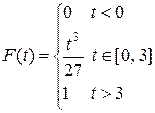 .
. .
. .
. найдем, воспользовавшись формулой
найдем, воспользовавшись формулой .
.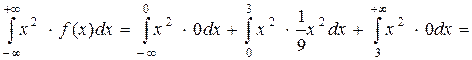
 .
.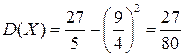 .
.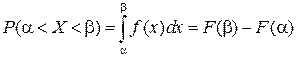 .
. .
. ,
, , 4)
, 4)  .
. . Найти
. Найти  . Найти
. Найти  .
. .
. .
. . Построить графики функций
. Построить графики функций  и
и  .
. . Ответ.
. Ответ.  .
. . Ответ. 1.
. Ответ. 1.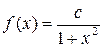 . Найти коэффициент c. Ответ.
. Найти коэффициент c. Ответ.  .
. . Найти вероятность
. Найти вероятность  . Ответ.
. Ответ.  .
. .Найти вероятность
.Найти вероятность  . Ответ.
. Ответ. 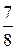 .
. .
. .
. . Найти коэффициент с и М(X). Ответ.
. Найти коэффициент с и М(X). Ответ.  .
. .Найти математическое ожидание М(X). Ответ.
.Найти математическое ожидание М(X). Ответ.  .
. .
. .
.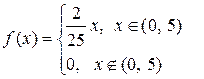 . Найти дисперсию
. Найти дисперсию  .
. .
. . Ответ.
. Ответ.  .
. . Ответ.
. Ответ. 
 .
.

 . Найти математическое ожидание и дисперсию объема куба.
. Найти математическое ожидание и дисперсию объема куба.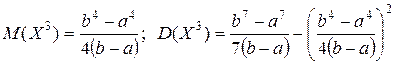 .
. . Найдите математическое ожидание площади диска. Ответ.
. Найдите математическое ожидание площади диска. Ответ.  .
.
 . Ответ.
. Ответ. 



