
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Практические занятия № 14 – 15Содержание книги Поиск на нашем сайте
Тема 1: «Алгебра событий»
Задача 1. Произведено два выстрела по мишени. Описать пространство элементарных событий. Описать через элементарные события следующие события: А – допущен хотя бы один промах и В – было два попадания. Являются ли события А и В совместными? Противоположными? Решение. Пространство элементарных событий: { Задание. Игральную кость бросают один раз. а) Описать пространство элементарных событий; б) Указать, из каких элементарных событий состоят события: А– (выпало нечетное число очков), В – (выпало число очков, кратное трем), С – (Выпало не более четырех очков), D – (выпало не менее трех и не более пяти очков); в) Описать события: А+С, В∙D,
Тема 2: «Непосредственный подсчет вероятностей»
Задача 2. Прибор состоит из трех блоков. События Задание. Стрелок стреляет по мишени два раза. Какие из перечисленных ниже событий являются совместными: Задача 3. Из 60 вопросов к экзамену студент выучил 50. В билете 3 вопроса. Какова вероятность события А: студент выучил все вопросы билета? События В: студент выучил хотя бы один вопрос билета? Решение. Воспользуемся формулой: Чтобы найти вероятность события В воспользуемся формулой
Задание. 1. Бросают две игральные кости, Найти вероятность того, что сумма выпавших очков будет не более 3. Ответ. 2. Бросают 4 игральные кости. Найти вероятность того, что на них выпадет по одинаковому числу очков. Ответ. 3. В партии из 20 деталей 16 стандартных. Наудачу выбираются три детали. Найти вероятности событий А- все три детали стандартны; В – все детали нестандартны. С – две детали стандартны; D – одна деталь стандартна. Ответ.
4. Кубик с окрашенными гранями разрезан на 1000 одинаковых маленьких кубиков, которые затем перемешиваются. Наудачу вынимается один кубик. Найти вероятности событий А – у кубика окрашена одна грань; В – у кубика окрашены две грани; С – у кубика окрашены три грани; D – кубик не окрашен. Ответ. 5. В ящике находятся 6 красных, 5 синих и 4 желтых шара. Наудачу вынимаются два шара. Найти вероятности событий: А – вынуты два шара одного цвета; В – вынуты два шара разного цвета; С – среди вынутых шаров нет синих. Ответ. 6. На складе находятся 10 телевизоров, из них 4 фирмы «Витязь». Найти вероятность того, что из 5 наудачу отобранных телевизоров ровно 2 будут фирмы «Витязь». Ответ. 7. Найти вероятность того, что дни рождения 12 случайно выбранных людей придутся на разные месяцы года. Ответ. 8. Для уменьшения общего числа игр 16 хоккейных команд разбиты на две подгруппы по 8 команд в каждой. Найти вероятность того, что две наиболее сильные команды а) окажутся в разных подгруппах; б) окажутся в одной подгруппе. Ответ. а) 9. В урне 10 шаров занумерованных числами 1, 2,…,10. Из урны наудачу вынимается шар и записывается его номер. Затем шар откладывается в сторону и из урны вынимается второй шар. Найти вероятность того, что номер второго шара больше, чем номер первого шара. Ответ. 0,5 10. Монета бросается три раза. Найти вероятность того, что герб выпадет хотя бы один раз. Ответ. 11. В коробке 5 одинаковых изделий, причем 3 из них окрашено. Найти вероятность того, что из 2 наугад отобранных изделий а) ровно одно окрашено; б) хотя бы одно окрашено. Ответ. а) 0,6 б) 0.9. 12. Из 12 лотерейных билетов 4 выигрышных. Наудачу берут 6 билетов. Какова вероятность того, что среди них будет хоть один выигрышный? Ответ. 0,96.
Тема 3: «Геометрическая вероятность»
Задача 4. На отрезок L длиной 20см наудачу помещен отрезок l длиной 5см. Найти вероятность того, что точка, наудачу поставленная на L попадет также и на отрезок l. Решение. Задание. 13. На отрезке ОА длины L наугад ставится точка В. Найти вероятность того, что меньший из отрезков ОВ и ВА имеет длину не меньше чем L/3. Ответ. 1/3.
14. В круг радиуса R наудачу помещен круг меньшего радиуса r. Найти вероятность того, что точка, наудачу поставленная в круг R, попадет также и в круг r. Ответ. 15. Плоскость разграфлена параллельными прямыми, расстояние между которыми равно 2а. На плоскость наудачу брошена монета радиуса 16. На плоскость с нанесенной сеткой квадратов со стороной а наудачу брошена монета радиуса 17. Внутри квадрата с вершинами в точках (0; 0), (0; 1), (1; 0), (1; 1) наудачу выбрана точка М с координатами (х; у). Найти вероятность событий А: Ответ. 18. На отрезок АВ длиной 10см наугад бросают точку М. Какова вероятность того, что площадь квадрата со стороной АМ будет больше 25см² и меньше 64см²? Ответ. 0,09. 19. На отрезке ОА длины L числовой оси ОХ наудачу ставятся точки В(х) и С(у), причем
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 16 Тема:« Теоремы сложения и умножения вероятностей»
При решении задач этой темы используются формулы:
Задача 1. Два стрелка стреляют по одной и той же цели. Вероятности поражения ими цели равны соответственно 0,7 и 0,8. Какова вероятность поражения цели? Решение. Пусть событие А – поражение цели первым стрелком, событие В – поражение цели вторым стрелком. Тогда Р(А) =0,7, Р(В) =0,8,
Ответ. 0,94 Задание. 1. Два стрелка стреляют по одной мишени. Вероятность попадания в мишень равна 0,6 для первого стрелка и 0,7 для второго стрелка. Найти вероятность того, что в мишень попадет только один стрелок. Ответ. 0,46. 2. Вероятность одного попадания в цель при одном залпе двух стрелков равна 0,38. Известно, что вероятность попадания в цель при одном выстреле для первого стрелка равна 0,8. Найти вероятность попадания в цель при одном выстреле для второго стрелка. Ответ. 0,7. 3. Для предупреждения пожара установлено два сигнализатора, работающих независимо друг от друга. Вероятность того, что при пожаре сработает первый сигнализатор, равна 0,9, для второго сигнализатора эта вероятность равна 0,95. Найти вероятность того, что при пожаре сработает только один сигнализатор. Ответ. 0,14 4. Вероятность того, что при одном измерении некоторой физической величины будет допущена ошибка, превышающая заданную точность, равна 0,4. Произведено три независимых измерения. Найти вероятность того, что только в одном из них будет допущена ошибка, превышающая заданную точность. Ответ. 0,432. 5. При стрельбе из пистолета вероятность попадания в «десятку» равна 0,25; в «девятку» - 0,30; в «восьмерку» - 0,15; в «семерку» - 0,12. Найти вероятность того, что стрелок, сделав один выстрел, выбьет: а) не менее 8 очков; б) не более 8 очков? Ответ. а) 0,70; б) 0,45. 6. Студент разыскивает нужную ему формулу в трех справочниках. Вероятность того, что формула находится в первом справочнике, равна 0,6; во втором – 0,7; в третьем – 0,8. Найти вероятность того, что нужная формула находится: а) только в одном справочнике; б) только в двух справочниках; в) во всех трех справочниках; г) нет ни в одном справочнике. Ответ. а) 0,188; б) 0,452 в) 0,336; г) 0,024.
Задача 2. Сколько надо бросить игральных костей, чтобы с вероятность того, что ни на одной из костей не выпадет 6 очков, стала бы меньше, чем 0,3? Решение. Пусть событие
7. Вероятность выигрыша лотерейного билета равна 8. Вероятность попадания в мишень при одном выстреле равна 0,8. Сколько надо сделать выстрелов, чтобы вероятность того, что не будет ни одного промаха, стала бы меньше, чем 0,4? Ответ. Не менее 5. Задача 3. Найти вероятность работы схемы, если вероятность работы каждого отдельного элемента равна 0,8.
Решение. Схема представляет собой параллельное соединение подсхем А и В
Подсхема А представляет собой последовательное соединение двух элементов, а подсхема В представляет собой последовательное соединение трех элементов.
Тогда: вероятность работы подсхемы А: Р(А)=0,8 ∙0,8=0,64 вероятность отказа подсхемы А: вероятность работы подсхемы В: вероятность отказа подсхемы В: вероятность отказа всей схемы: вероятность работы всей схемы: Ответ. 0,82432.
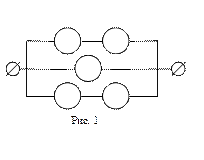
Задание. Найти вероятность работы схем (рис. 1 – 6), если вероятность работы каждого отдельного элемента равна 0,8. Ответ округлить до 0,0001.
Ответ. 1) 0,974; 2) 0,952; 3) 0,737; 4) 0,788; 5) 0,733; 6) 0,594.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 17 Тема: «Формула полной вероятности. Формула Бейеса»
Задача 1. В коробке находятся 3 новых и 3 уже использованных теннисных мяча. Для первой игры наудачу берут из коробки 2 мяча, затем их возвращают в коробку. Какова вероятность для второй игры вынуть наудачу из этой коробки два новых мяча? Решение. Пусть событие А= {вынуть два новых мяча для второй игры}. Ситуация перед второй игрой описывается следующими гипотезами:
Найдем условные вероятности события А в случае осуществления каждой гипотезы:
Теперь, используя формулу полной вероятности, найдем
Ответ. Задание. 1.В первом ящике было 3 белых и 8 черных шаров, во втором ящике – 6 белых и 5 черных. Из первого ящика во второй переложили наудачу взятый шар. Какова теперь вероятность вынуть черный шар: а) из первого ящика? б) из второго ящика? Ответ. а) 2. В первом ящике 10 шаров, из них 8 белых; во втором ящике 20 шаров, из них 4 белых. Из каждого ящика наудачу извлекли по шару, после чего из этих двух шаров выбрали один. Какова вероятность того, что был выбран белый шар? Ответ. 0,5 3. В ящике было 9 шаров. В ящик положили белый шар, шары перемешали, после чего из ящика наудачу вынули один шар. Какова вероятность того, что вынутый шар белый, если все предположения о цвете шаров в ящике равновероятны? Ответ. 0,45. 4. В ящике содержатся 12 деталей, изготовленных на заводе №1, 20 деталей производства завода №2 и 18 деталей завода №3. Вероятность того, что деталь отличного качества равна для 1-го, 2-го т 3-го заводов 0,9, 0,6 и 0,9 соответственно. Найти вероятность того, что наудачу извлеченная из ящика деталь будет отличного качества. Ответ. 0,78. 5. Из 12 лотерейных билетов было 4 выигрышных. Какова вероятность вытянуть выигрышный билет, если перед этим было вытянуто два билета? Ответ. 0, 26. 6. Группа состоит из двух отличных, 4 хороших и 4 посредственных стрелков. Вероятность попадания в цель при одном выстреле равна 0,9, 0,75 и 0,6 для отличного, хорошего и посредственного стрелка соответственно. Наугад выбранный стрелок выстрелил в цель. Какова вероятность поражения мишени? Ответ. 0,72.
Задача 2. В коробке находятся 3 новых и 3 уже использованных теннисных мяча. Для первой игры наудачу берут из коробки 2 мяча, затем их возвращают в коробку. Для второй игры вынули два новых мяча. Какова вероятность того, что при этом для первой игры вынули два уже использованных мяча? Решение. Пусть событие А = {вынуть два новых мяча для второй игры}. Ситуация перед второй игрой описывается следующими гипотезами:
В ходе решения задачи 1 были найдены:
Таким образом 7. В ящике было 3 белых и 7 черных шаров. Один шар вынули наудачу и отложили в сторону. Следующий вынутый шар оказался белым. Какова вероятность того, что и первый шар был белым? Ответ. 8. Из 12 лотерейных билетов 5 выигрышных. Билеты вынимаются наудачу по одному. Во второй раз был вытянут выигрышный билет. Какова вероятность того, что и в первый раз был вытянут выигрышный билет? Ответ. 9. Число грузовых машин, проезжающих мимо АЗС относится к числу легковых машин как 3:2. Вероятность того, что грузовая машина заедет на заправку, равна 0,1; для легковой машины эта вероятность равна 0,2. К АЗС подъезжает на заправку машина. Какова вероятность того, что это грузовик? Ответ.
10. Группа состоит из двух отличных, 4 хороших и 4 посредственных стрелков. Вероятность попадания в цель при одном выстреле равна 0,9, 0,75 и 0,6 для отличного, хорошего и посредственного стрелка соответственно. Наугад выбранный стрелок выстрелил в цель и попал в мишень. Какова вероятность того, что стрелял отличный стрелок? Ответ. 11. Три стрелка произвели залп, причем в цель попало две пули. Вероятности попадания стрелков равны 0,6, 0,5 и 0,4. Найти вероятность того, что третий стрелок попал в цель. Ответ.
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 1102; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.122.145 (0.009 с.) |

 - попадание при первом выстреле;
- попадание при первом выстреле;  - попадание при втором выстреле}. Тогда событие А =
- попадание при втором выстреле}. Тогда событие А =  ; событие В =
; событие В =  . События А и В несовместны и не являются противоположными.
. События А и В несовместны и не являются противоположными.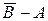 ,
, 
 - работает первый, второй и третий блок соответственно. Событие А – прибор работает. Описать событие А через события
- работает первый, второй и третий блок соответственно. Событие А – прибор работает. Описать событие А через события  -хотя бы одно попадание;
-хотя бы одно попадание;  - хотя бы один промах;
- хотя бы один промах;  - ровно два попадания;
- ровно два попадания;  - ни одного попадания.
- ни одного попадания. . Тогда
. Тогда  - число вариантов выбора трех вопросов из 60.
- число вариантов выбора трех вопросов из 60.  - число благоприятных вариантов выбора трех вопросов из 50 выученных. Получается
- число благоприятных вариантов выбора трех вопросов из 50 выученных. Получается 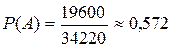 .
.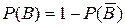 , где событие
, где событие 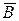 - студент не выучил ни одного вопроса билета, т.е. событие, противоположное событию В.
- студент не выучил ни одного вопроса билета, т.е. событие, противоположное событию В.  ;
;  . Тогда
. Тогда  . Ответ. 0,572; 0,997.
. Ответ. 0,572; 0,997. .
. .
.
 .
. .
. .
. .
. б)
б)  .
. .
. .
. .
. . Найти вероятность того, что монета не пересечет ни одну из параллельных прямых. Ответ.
. Найти вероятность того, что монета не пересечет ни одну из параллельных прямых. Ответ.  .
. . Найти вероятность того, что монета не пересечет ни одну из сторон квадрата. Ответ.
. Найти вероятность того, что монета не пересечет ни одну из сторон квадрата. Ответ.  .
. , В:
, В:  , С:
, С:  .
. .
. . Найти вероятность того, что длина отрезка ВС меньше L/2. Ответ. 3/4.
. Найти вероятность того, что длина отрезка ВС меньше L/2. Ответ. 3/4.

 . Событие С – поражение мишени описывается через события А и В следующим образом:
. Событие С – поражение мишени описывается через события А и В следующим образом:  . Так как слагаемые представляют собой несовместные события, то
. Так как слагаемые представляют собой несовместные события, то .
. состоит в том, что на i- ой кости не выпало 6 очков. Тогда
состоит в том, что на i- ой кости не выпало 6 очков. Тогда  .Вероятность того, что при бросании n костей на них не выпадет ни одной «6», равна
.Вероятность того, что при бросании n костей на них не выпадет ни одной «6», равна  . Чтобы найти n, надо решить неравенство
. Чтобы найти n, надо решить неравенство  , откуда
, откуда  . Ответ.
. Ответ.  . Сколько надо купить лотерейных билетов, чтобы вероятность того, что хотя бы один билет выиграет, стала бы больше, чем 0,8? Ответ. Не менее 8.
. Сколько надо купить лотерейных билетов, чтобы вероятность того, что хотя бы один билет выиграет, стала бы больше, чем 0,8? Ответ. Не менее 8.


 .
. .
. .
. .
. .
.





 ={в коробке один новый мяч}, если для первой игры вынули два новых мяча;
={в коробке один новый мяч}, если для первой игры вынули два новых мяча;  ={в коробке два новых мяча}, если для первой игры вынули один новый и один уже использованный мяч;
={в коробке два новых мяча}, если для первой игры вынули один новый и один уже использованный мяч;  ={В коробке три новых мяча}, если в первой игре играли уже использованными мячами. Гипотезы
={В коробке три новых мяча}, если в первой игре играли уже использованными мячами. Гипотезы  ;
;  ;
;  .
. ;
;  ;
;  .
.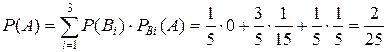 .
.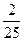 .
. ; б)
; б)  .
.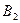 ={в коробке два новых мяча}, если для первой игры вынули один новый и один уже использованный мяч;
={в коробке два новых мяча}, если для первой игры вынули один новый и один уже использованный мяч; 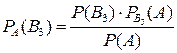
 ;
;  .
. . Ответ.
. Ответ. 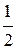 .
. .
. .
.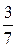
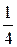 .
.



