
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математические методы в экономикеСодержание книги
Поиск на нашем сайте
15.1. Сетевое планирование. Прогресс производства сложной продукции разбивается на отдельные этапы, зашифрованные номерами 1, 2,..., 10. 1 – начальный этап производства продукции, 10 – завершающий. Переход от
15.1.3. Найдите критическое время завершения процесса работ Ткр и выделите стрелки, лежащие на критическом пути. 15.1.4. Для каждой некритической операции 15.1.5. Решите задачу табличным методом. Номера этапов, лежащие на критическом пути подчеркните. (В табличном методе кроме резервов свободного времени 15.1.6. Задача коммивояжёра. Требуется найти кратчайший из замкнутых маршрутов, проходящих точно по одному разу через каждый из шести городов
где с = m+n
15.2. В парикмахерский салон приходит в среднем 15.2.1. Найти относительную пропускную способность СМО 15.2.2. Найти доход 15.2.3. Найти аналогичные характеристики СМО
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 309; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.61.142 (0.006 с.) |

 -го этапа к
-го этапа к  -му этапу назовем операцией. Возможны выполнения операций
-му этапу назовем операцией. Возможны выполнения операций  и их продолжительности
и их продолжительности  задаются таблицей.
задаются таблицей. обозначить стрелками, проставляя над ними продолжительность
обозначить стрелками, проставляя над ними продолжительность 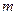

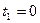 , определите время
, определите время  окончания каждого
окончания каждого 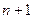

 и проставьте их над стрелками рядом с
и проставьте их над стрелками рядом с  для каждого этапа.)
для каждого этапа.) .Задана матрица расстояний между любыми парами городов, причём расстояние от города
.Задана матрица расстояний между любыми парами городов, причём расстояние от города  до города
до города  может не совпадать с расстоянием от
может не совпадать с расстоянием от  считается равным расстоянию от
считается равным расстоянию от  Системы массового обслуживания (СМО).
Системы массового обслуживания (СМО). клиента в час (т.е. интенсивность
клиента в час (т.е. интенсивность 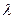 поступления заявок в систему равна
поступления заявок в систему равна 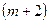 /час), а среднее время обслуживания одного клиента равно 1/
/час), а среднее время обслуживания одного клиента равно 1/ 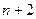 тысяч рублей в час.
тысяч рублей в час. (т.е. вероятность того, что поступившая заявка будет обслужена) и абсолютную пропускную способность СМО
(т.е. вероятность того, что поступившая заявка будет обслужена) и абсолютную пропускную способность СМО  (число заявок, обслуживаемых за 1 час), если салон обслуживает два мастера.
(число заявок, обслуживаемых за 1 час), если салон обслуживает два мастера. , полученный за 1 час работы двух мастеров.
, полученный за 1 час работы двух мастеров. ,
,  и
и 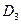 , когда салон обслуживают три мастера, и определить, выгодно ли принять на работу третьего мастера с точки зрения общего дохода, полученного за 1 час работы салона.
, когда салон обслуживают три мастера, и определить, выгодно ли принять на работу третьего мастера с точки зрения общего дохода, полученного за 1 час работы салона.


