
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частные производные и дифференциал функции.Содержание книги
Поиск на нашем сайте
5.1.1.Найти частные производные 5.1.2.Найти дифференциал 5.1.3.Показать, что функция Приложения частных производных. 5.2.1.Составить уравнения касательной плоскости и нормали к поверхности 5.2.2.Для функции
Двойные, тройные и криволинейные интегралы Двойные интегралы. 6.1.1.Изменить порядок интегрирования:
6.1.2.Сделать чертеж и найти объем тела, ограниченного поверхностями 6.1.3.Сделать чертеж и найти площадь фигуры, ограниченной линиями: а) Тройные интегралы. 6.2.1.Найти 6.2.2.Найти объем тела, ограниченного поверхностями Криволинейные интегралы. 6.3.1.Вычислить 6.3.2.Вычислить
Элементы теории поля Дифференциальные операции. 7.1.1.В точке
7.1.2.Найти в точке
7.1.3.Найти в точке
7.1.4.Найти в точке
Интегралы и интегральные теоремы. 7.2.1.Убедиться, что поле 7.2.2.Даны поле а) поток поля б) поток поля 7.2.3. Даны поле
Дифференциальные уравнения Уравнения первого порядка. 8.1.1.Найти общее решение уравнения: а) 8.1.2.Скорость роста банковского вклада пропорциональна с коэффициентом равным
Линейные уравнения высших порядков. 8.2.1.Решить задачу Коши: а) б) Системы линейных уравнений. 8.3.1.Решить систему линейных уравнений
Ряды Числовые ряды. 9.1.1.Исследовать на сходимость ряды с положительными членами: а) в) 9.1.2.Исследовать на условную сходимость и абсолютную сходимость знакочередующиеся ряды: а) Степенные ряды. 9.2.1.Найти область сходимости степенного ряда: а)
9.2.2.Разложить функцию а) 9.2.3.С помощью разложения в ряд вычислить приближенно с точностью 0,001 значения: а) Ряды Фурье. 9.3.1.Разложить функцию а) в интервале б) в)
|
|||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 304; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.126.36 (0.009 с.) |

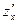 ,
,  и
и 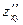 функций:
функций: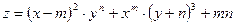 ; б)
; б) 
 функции
функции  .
.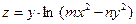 удовлетворяет уравнению
удовлетворяет уравнению  .
. в точке
в точке 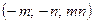 .
.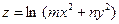 в точке
в точке 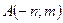 найти градиент и производную по направлению
найти градиент и производную по направлению  .
.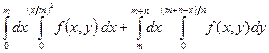 .
. и плоскостью, проходящей через точки
и плоскостью, проходящей через точки 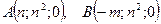 и
и  .
. .
. , если тело V ограниченно плоскостями
, если тело V ограниченно плоскостями  и
и  .
. .
. , где
, где 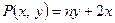 ,
, 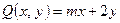 , а контур С образован линиями
, а контур С образован линиями  ,
, 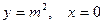 : а) непосредственно; б) по формуле Грина.
: а) непосредственно; б) по формуле Грина. , где контур С является одним витком винтовой линии:
, где контур С является одним витком винтовой линии: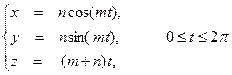 .
.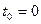 составить уравнение касательной прямой и нормальной плоскости к кривой
составить уравнение касательной прямой и нормальной плоскости к кривой .
.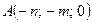 градиент скалярного поля
градиент скалярного поля .
.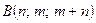 дивергенцию векторного поля
дивергенцию векторного поля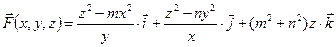 .
.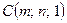 ротор векторного поля
ротор векторного поля .
. потенциально, и найти его потенциал.
потенциально, и найти его потенциал. и цилиндр D, ограниченный поверхностями z=0, z=m, x2+y2=(n+1)2. Найти:
и цилиндр D, ограниченный поверхностями z=0, z=m, x2+y2=(n+1)2. Найти: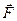 через боковую поверхность цилиндра в направлении внешней нормали;
через боковую поверхность цилиндра в направлении внешней нормали;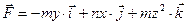 и замкнутый виток
и замкнутый виток  ,
,  (обход контура происходит в направлении, соответствующем возрастанию параметра φ). Найти циркуляцию поля
(обход контура происходит в направлении, соответствующем возрастанию параметра φ). Найти циркуляцию поля  ; б)
; б) 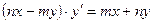 ; в)
; в)  .
.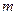 величине вклада. Найти закон изменения величины вклада со временем, если первоначальная сумма вклада составляла
величине вклада. Найти закон изменения величины вклада со временем, если первоначальная сумма вклада составляла  миллионов рублей.
миллионов рублей.
 .
.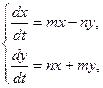 с начальными условиями
с начальными условиями  .
. ; б)
; б) 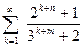 ;
; ; г)
; г) 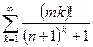 .
. ; б)
; б) 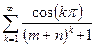 .
. ; б)
; б)  .
. в ряд Тейлора в окрестности точки х0:
в ряд Тейлора в окрестности точки х0: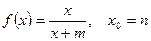 ; б)
; б) 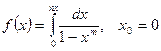 .
. ; б)
; б)  .
.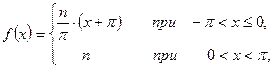
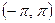 ;
;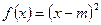 в интервале
в интервале 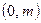 .
.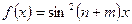 в интервале
в интервале 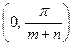 .
.


