
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача оптимального производства продукции.Содержание книги
Поиск на нашем сайте
Предприятие планирует выпуск двух видов продукции I и II, на производство которых расходуется три вида сырья А, В, и С. Потребность
14.1.1. Для производства двух видов продукции I и II с планом 14.1.2. В условиях задачи 14.1.1. составить оптимальный план 14.1.3. Построить по полученной системе ограничений многоугольник допустимых решений и найти оптимальный план производства геометрическим путем. Определить соответствующую прибыль Транспортная задача. На трех складах
14.2.1. Сравнивая суммарный запас 14.2.2. Составить первоначальный план перевозок. (Рекомендуется воспользоваться методом наименьшей стоимости.) 14.2.3. Проверить, является ли первоначальный план оптимальным в смысле суммарной стоимости перевозок, и если это так, то составить оптимальный план
обеспечивающий минимальную стоимость перевозок Матричные игры. 14.3.1. Игра
Найти вероятности применения стратегий 1-м и 2-м игроком для получения цены игры. (Задачу решить аналитическим методом.) 14.3.2. Игра задана матрицами
и
Применяя графический метод, найти смешанные оптимальные стратегии обоих игроков и определить цену игры.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 635; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.109.141 (0.005 с.) |

 на каждую единицу
на каждую единицу  -го вида продукции
-го вида продукции  -го вида сырья, запас
-го вида сырья, запас 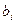 соответствующего вида сырья и прибыль
соответствующего вида сырья и прибыль 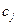 от реализации единицы
от реализации единицы 


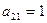
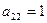


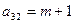


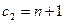
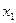

 единиц обоих видов продукции.
единиц обоих видов продукции.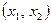 производства продукции, обеспечивающий максимальную прибыль
производства продукции, обеспечивающий максимальную прибыль  . Определить остатки каждого вида сырья. (Задачу решить симплекс – методом)
. Определить остатки каждого вида сырья. (Задачу решить симплекс – методом) ,
,  и
и  хранится
хранится  ,
,  и
и  единиц одного и того же груза. Этот груз требуется доставить трем потребителям
единиц одного и того же груза. Этот груз требуется доставить трем потребителям  ,
,  и
и  , заказы которых составляют
, заказы которых составляют  ,
, 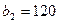 и
и  единиц груза соответственно. Стоимость перевозок
единиц груза соответственно. Стоимость перевозок  единицы груза с
единицы груза с  потребности
запасы
потребности
запасы
 4
4

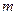

 5
5
 3
3
 1
1


 и суммарную потребность
и суммарную потребность  в грузе, установить, является ли модель транспортной задачи, заданная этой таблицей, открытой или закрытой. Если модель является открытой, то ее необходимо закрыть, добавив фиктивный склад
в грузе, установить, является ли модель транспортной задачи, заданная этой таблицей, открытой или закрытой. Если модель является открытой, то ее необходимо закрыть, добавив фиктивный склад  с запасом
с запасом 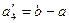 в случае
в случае  или фиктивного потребителя
или фиктивного потребителя  с потребностью
с потребностью  в случае
в случае  и положив соответствующие им тарифы перевозок нулевыми.
и положив соответствующие им тарифы перевозок нулевыми. ,
, . Найти эту стоимость. (Рекомендуется воспользоваться методом потенциалов.)
. Найти эту стоимость. (Рекомендуется воспользоваться методом потенциалов.)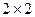 задана матрицей
задана матрицей
 для
для  для
для 


