
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Собственные числа и собственные векторы.Содержание книги
Поиск на нашем сайте
Найти собственные числа и соответствующие им собственные векторы для матрицы
Аналитическая геометрия Прямая на плоскости. Построить треугольник, вершины которого находятся в точках 1) координаты точки пересечения медиан; 2) длину и уравнение высоты, опущенной из вершины А; 3) площадь треугольника; 4) систему неравенств, задающих внутренность треугольника АВС. Кривые второго порядка на плоскости. Составить уравнение кривой, для каждой точки которой отношение расстояния до точки Прямая и плоскость в пространстве. Дана треугольная пирамида с вершинами в точках a) уравнение плоскости, проходящей через точки А, В и С; б) величину угла между ребром SC и гранью АВС; в) площадь грани АВС; г) уравнение высоты, опущенной из вершины S на грань АВС, и ее длину; д)объем пирамиды SАВС. Дифференциальное исчисление Пределы, непрерывность и разрывы функций. 3.1.1.Найти пределы функций: а) б) в) г) 3.1.2.В точках
Производные функций. 3.1.3.Найти производные а) в) ж)
Приложения производной. 3.2.1.С помощью методов дифференциального исчисления построить графики функций: 3.2.2.Найти наибольшее и наименьшее значение функции Приближенное решение алгебраических уравнений. 3.3.1.Для уравнения а) методом деления отрезка пополам; б) методом касательных. Примечание. Можно считать, что точность
Интегральное исчисление
Неопределенный интеграл. 4.1.1.Найти интегралы:
д)
Несобственные интегралы. 4.2.1.Вычислить интеграл или установить его расходимость:
Применения определенных интегралов. 4.3.1.Построить схематический чертеж и найти площадь фигуры, ограниченной линиями:
4.3.2.Найти объем тела, полученного при вращении вокруг оси ОХ фигуры, ограниченной линиями:
Приближенное вычисление определенных интегралов. 4.4.1.Для вычисления определенного интеграла
Функции нескольких переменных
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 271; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.43.92 (0.008 с.) |

 .
. ,
,  ,
,  и найти:
и найти: к расстоянию до прямой
к расстоянию до прямой  равно
равно  . Привести уравнение к каноническому виду и определить тип кривой.
. Привести уравнение к каноническому виду и определить тип кривой. ,
,  ,
,  ,
,  ,. Найти:
,. Найти: ;
;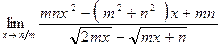 ;
; ;
;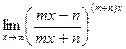 .
. и
и  для функции
для функции  установить непрерывность или определить характер точек разрыва. Нарисовать график функции
установить непрерывность или определить характер точек разрыва. Нарисовать график функции  ;
; функций:
функций: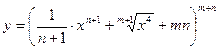 ; б)
; б)  ;
;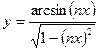 ; д)
; д)  ; е)
; е)  ;
;
 ; б)
; б) 
 на отрезке
на отрезке 
 отделить положительный корень и найти его приближенно с точностью
отделить положительный корень и найти его приближенно с точностью  :
: достигнута, если разность между соседними приближениями
достигнута, если разность между соседними приближениями  и
и 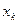 удовлетворяет неравенству
удовлетворяет неравенству  .
. б)
б) 
 г)
г)  ;
;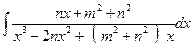 ; е)
; е)  .
.
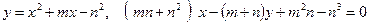 ;
; .
. , разбивая отрезок интегрирования сначала на 10 равных частей, а затем на 20 равных частей, найти приближенное значение
, разбивая отрезок интегрирования сначала на 10 равных частей, а затем на 20 равных частей, найти приближенное значение 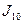 и
и  : а) по формуле трапеций; б) по формуле Симпсона. Оценить точность приближения с помощью разности
: а) по формуле трапеций; б) по формуле Симпсона. Оценить точность приближения с помощью разности  .
.


