
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоретический уровень научного знанияСодержание книги
Поиск на нашем сайте
Эмпирический уровень научного знания организован довольно просто -- в нем есть факты разных уровней, обобщенные факты - эмпирические закономерности и некоторые простейшие гипотезы. Но главным является именно понятие факта Теоретический уровень является значительно более сложным. В нем ``живут'' гипотезы разного уровня сложности, концепции, теории, исследовательские программы. Большую популярность в последние лет двадцать приобрело понятие ``парадигма''. Очень интересным структурным образованием теоретического уровня научного знания является научная картина мира. Некоторые, но не все, из этих понятий будут обсуждаться в нашем курсе. Но основным понятием является все же понятие теории. И именно оно будет в центре внимания нашего курса. Теория Основным вопросом данного раздела курса является вопрос -- что такое теория? Раньше уже говорилось, что термин ``теория'' очень многозначен. В самом широком смысле (и в этом плане почти лишенным смысла) термином ``теория'' обозначают любой продукт рационального мышления. Но в таком расширительном смысле его просто невозможно обсуждать, тем более, если речь идет о философии науки. Дело в том, что и обыденное знание основано на рациональном мышлении, и в этом случае сам термин ``наука'' лишается смысла. В несколько более узком смысле теорией называют все, что не является констатацией единичного факта. Именно так термин ``теория'' употребляется почти во всех произведениях (не могу назвать их работами -- это именно произведения, тексты, часто даже бессмысленные) далеких от философии науки. Но иногда этот смысл термина возникает и в философии науки. Но заметим, что в этом смысле эмпирическая закономерность -- тоже теория. Для людей, плохо знающих, что такое наука, это может быть и простительно. Но мы, люди, знающие науку изнутри, никогда не допустим такой ошибки. Мы прекрасно понимаем различие между эмпирической закономерностью и теорией. Поэтому в целях дальнейшего серьезного анализа нужно дать определение теории. Конечно, это определение не имеет строго логического характера. Это не формальное определение, а, скорее, разъяснение. И я думаю что такое разъяснение будет понятно и полезно тем, кто уже имеет хорошую практику обращения с теориями. Я предлагаю вашему вниманию следующее определение -разъяснение. Теория -- это целостная концептуальная символическая система (т.е. она основывается на некоторых концептуальных представлениях и выражена в символической форме, в виде символов). В этой системе определены (заданы) отношения так, что эта символическая система может быть отображением некоторого круга явлений природы, или, как иногда говорят, некоторого фрагмента или аспекта материального мира. Или иначе, теория есть идеальная модель некоторого фрагмента мира. Идеальная -- это значит, что она существует не в предметах, а в символах, в человеческом сознании. Теория есть идеализированная модель. Это значит, что любая теория отвлекается от тех сторон реальности, которые для данного круга явлений являются (или, по крайней мере, предполагаются) неизвестными. Теория является приближенной моделью. Это значит, что даже в данной области явлений теория не охватывает тех аспектов, о которых мы сейчас не знаем. Итак:
Все эти аспекты теории -- и то, что теория есть модель, и то, что она -- идеальная модель, и то, что теория -- приближенная модель, будут очень существенны для дальнейшего анализа. Пожалуй, лишь идеализированность теории не будет играть существенной роли в дальнейшем рассмотрении. Структура теории Я говорил, что теория -- это система, в которой заданы отношения. Это значит, что теория обладает структурой. Собственно говоря, наличие отношений и структурность -- это одно и то же. Так какова же структура научной теории? Я написал, и сейчас же хочу принести читателям свои извинения. Я написал ``научная теория'', но с моей точки зрения -- это плеоназм, избыточное выражение (типа: глупый дурак). Теории бывают только научными. Ненаучных теорий не бывает. Но в языке термин ``научная теория'' очень укоренился, поэтому я в дальнейшем буду использовать его наряду со словом ``теория'' просто, без прибавления эпитета ``научная''. Так какова же структура теории? Полное рассмотрение структуры научной теории не входит в нашу задачу. Да и вообще, такое рассмотрение нужно делать для каждой конкретной теории. Мы выделим только основные классы структурных компонентов теории, обладающих инвариантностью. Т.е. каждая научная теория включает в себя все эти классы. При этом я хочу сразу предупредить, что выделение каждого класса связано с весьма нетривиальными, а иногда и спорными проблемами философии науки. Некоторые из этих проблем мы будем обсуждать по ходу нашего изложения, а некоторые я намерен вынести в отдельное обсуждение. Первый класс структурных элементов теории -- это теоретические объекты, т.е. основные понятия, на которых строится теория, выраженные в символах. Так, в классической механике теоретическими объектами являются пространство, время, движение, скорость, ускорение, масса, импульс, сила, работа, энергия - кинетическая и потенциальная и пр. В общем, я думаю, что каждый из вас, зная какую-то теорию, легко выделит всю совокупность тех основных понятий, на которых основана данная теория. В этом смысле класс структурных элементов, образующих теории довольно прост и большого интереса не представляет. Очень интересная и принципиальная проблема возникает тогда, когда ставится вопрос о соответствии теоретических объектов реальности, т.е. об их теоретико-познавательном статусе. Эта проблема связана с весьма распространенными в неопозитивизме концепциями, если не скажи шире -- с общепозитивистской концепцией места теоретического уровня в познании в целом. Но мы не будем сейчас рассматривать эту проблему, а отложим ее обсуждение до конца данного раздела курса. Вторым структурным компонентом теории является ее аппарат, т.е. способ оперирования теоретическими объектами. И здесь я намерен выдвинуть и защищать позицию, состоящую в том, что аппарат теории -- это обязательно математический аппарат. Только математизированная система заслуживает названия теории. Нематематизированных теорий не бывает. Нематематизированные конструкции в науке присутствуют, более того -- они вполне принадлежат к теоретическому уровню научного знания, но теориями не являются. Нет теории эволюции Дарвина, как нет и марксовской теории общественно исторического процесса. Это образования другого типа, нежели теория. И для таких образований есть давнее и вполне традиционное название -- концепция. Да, есть эволюционная концепция Дарвина, основанная на широком обобщении фактического материала, и есть марксовская концепция общества, но это не теории. Постараюсь раскрыть свою позицию полнее. И для этого, я хочу обратиться к вопросу о том, что такое математика. Я не намерен ставить, а тем более решать его в общем смысле -- это очень важная и принципиальная проблема философии математики. Философия математики не является предметом нашего курса. Я даже не являюсь специалистом в этой области -- я физик (и философ естествознания) и буду рассуждать именно как физик, который использует математику в своих целях. Так вот: математика -- это язык, в котором хорошо (может быть, не идеально, но хорошо) определены правила следования. Из А, В, С на основе системы правил Р, Q, R получаются вполне определенные следствия D, E, F и именно эти, а не какие-то другие X, Y или Z. И именно это обстоятельство позволяет проверять теорию. Нематематизированная концепция выражается в естественном языке и применяет обычные правила ``здравого смысла". Можно сказать, что концепция -- это словесный проект возможной будущей теории. Возможной -- то есть может быть да, а может быть и нет. Но обычный естественный язык -- это система с плохо определенными правилами следования. В нем нельзя сказать ``отсюда следует то-то", а можно и даже нужно говорить ``Отсюда может быть следует то-то, но может быть и не следует". Это означает, что к концепции нельзя применять те требования, которые мы предъявляем к теории. Ее нельзя проверять так, как мы проверяем теорию, но ее нельзя и опровергать. Точнее, ее можно все-таки и проверять и опровергать, но не так, как мы проверяем или опровергаем теорию. По сути дела, концепция является гипотезой, иногда довольно простой, а иногда и весьма сложной, но именно гипотезой. И то, что обычно называют следствием из концепции, на самом деле является не следствием в точном смысле слова, а дополнительной гипотезой. Конечно, эта дополнительная гипотеза должна не противоречить всей структуре концепции, но все же она является именно дополнительной гипотезой, а не следствием. В соответствии со всем сказанным, нужно отметить, что концепция не может делать того, что делает теория -- а именно предсказывать. Можно ли на основе ``теории Дарвина" предсказать какие новые виды живых существ появятся на земле в результате, скажем, изменения каких-то условий? Очевидно нельзя! Что же касается предсказаний ``теории Маркса", то мы знаем, чем это окончилось. И это вполне нормально, концепция и не предназначена для того, чтобы предсказывать. Это, конечно, не значит, что концепции вообще лишены предсказательной возможности. Предикторские свойства концепции -- это не то же самое, что предикторские свойства гущи от кофе "мокко'' урожая 1929 года. Но они существенно ограничены. Можно сказать даже более определенно -- если концепция представляет собой широкое обобщение опытных данных (например, концепция Дарвина), то ее предсказательные возможности примерно такие же, как и эмпирической закономерности. Т.е. она неплохо интерполирует недостающие промежуточные данные, но крайне ненадежна для экстраполяции. Из отстаиваемого мной тезиса о том, что только математический аппарат может быть аппаратом теории, можно сделать (с определенной степенью надежности) вывод о том, что если нет соответствующего математического аппарата, то теория и не может возникнуть. Напомню, что волновая концепция (гипотеза) света была выдвинута Хр.Гюйгенсом еще в XVII веке до ньютоновской корпускулярной концепции. Но волновая теория появилась только тогда, когда Френель разработал соответствующий математический аппарат -- в начале XIX века. Я думаю, что каждый естествоиспытатель легко сможет охарактеризовать структуру математического аппарата знакомой ему теории и я не буду останавливаться на этом вопросе. Интерес представляет другой аспект: при создании новой теории, отображающей какую-то новую область явлений может оказаться необходимым новый математический аппарат. Очевидно, что средствами теории обыкновенных дифференциальных уравнений, вполне адекватных механическим явлениям, нельзя описать ни электромагнитных явлений, ни, тем более, явлений микромира. Для этого требуются более сложные математические средства. В связи с этим я вспоминаю патетическое (и с его точки зрения) "убийственное'' возражение против развиваемой концепции науки: "ну, разве можно описать работу мозга дифференциальными уравнениями?'' Согласен, скорее всего, нельзя. Но кто сказал, что математический аппарат состоит только в применении дифференциальных уравнений? А почему не интегродифференциальных? Операторных? Или, вообще, в использовании теории категорий и функторов? И здесь возникает вопрос: когда мы приступаем к разработке теории некоторого нового круга явлений, имеем мы уже подходящую математическую теорию или нет? В подавляющем большинстве наших случаев оказывалось, что математика уже заготовила подходящую к этому случаю конструкцию, если не во вполне завершенном виде, то, по крайней мере, в той степени, когда можно эффективно продолжать работу. Но если такого и нет, то физики, не стесняясь, начинают сами создавать новый аппарат. Так было, когда Дирак начал использовать знаменитую Вторым очень интересным вопросом, связанным с использованием математического аппарата является наличие в физике эквивалентных описаний. Мы знаем, что любая развитая математизированная теория может быть выражена при помощи нескольких разных математических формализмов. Например, классическая механика может быть выражена в следующих формах: 1. Классическая геометрически-векторная форма, идущая от Ньютона. 2. Механика в форме Лагранжа. 3. Каноническая форма Гамильтона. 3а. Каноническая форма со скобками Пуассона. 4. Механика в форме принципа наименьшего действия Гамильтона. 4а. Принцип наименьшего действия в форме Мопертюи. 4в. ...в форме Лагранжа. 4с. ...в форме Якоби. 5. Классическая механика в форме уравнения в частных производных Гамильтона-Якоби. 6. Классическая механика в форме уравнения Лиувилля. 7. Механика в форме принципа виртуальных перемещений Д`Аламбера. 8. Механика в форме принципа наименьшего принуждения Гаусса. 9. Механика в форме принципа наименьшей кривизны Генриха Герца. Как видите, спектр разных формализмов классической механики очень широк. Для квантовой механики мне известно шесть разных формализмов. 1. Волновая механика Шредингера. 2. Матричная механика Гайзенберга. 3. Квантовая механика в формализме матрицы плотности. 4. Квантовая механика в формализме функций Вигнера и преобразования операторов Велья. 5. Формализм Фейнмана интегралов по всем траекториям. 6. Квантовая механика с ``пятым временем'' (новая разработка середины -- конца 70-тых годов). И такое можно сказать про любую теорию. Так что это -- разные теории или нет? В литературе по философии науки делалась попытка рассматривать различные эквивалентные описания как разные онтологии, т.е. как имеющие различный физический смысл. Я думаю, что это неверно. Дело в том, что все такие описания есть эквивалентные формы одной теории. Они переводятся друг в друга неособым (что очень важно) преобразованием и имеют один и тот же физический смысл. Но тогда возникает вопрос -- а зачем нужно столько эквивалентных формализмов? Тривиальный ответ состоит в том, что разные формализмы оказываются удобными для решения разных задач. Но это именно тривиально. Нетривиальный ответ на этот вопрос предложил знаменитый физик Ф.Дайсон. Но к его ответу мы вернемся позже. Обсуждение эквивалентных формализмов естественно подводит нас к вопросу о том, как используется математический аппарат в структуре теории. Этот вопрос обращает нас к следующему структурному компоненту теории. Таким компонентом являются связи между теоретическими объектами, устанавливаемые при помощи математического аппарата. Связи между теоретическими объектами можно разделить на две большие группа. Первая группа -- это связи-определения
-- это определение скорости.
-- это определение импульса в классической (или релятивистской) механике. A = -- это определение работы в механике. На основании связей-определений создается описание состояния физической системы. Механическая система описывается набором координат и скоростей материальных точек, точкой в 6 N -мерном фазовом пространстве и прочее. Квантовомеханическая система описывается волновой функцией 3 N -мерном конфигурационном пространстве, вектором состояния в счетномерном (или несчетномерном) Гильбертовом пространстве L 2, набором операторов наблюдаемых величин и пр. И, наконец, самый важный тип связей -- связи между состояниями системы. Эти связи суть уравнения, описывающие изменения системы. Очень хотелось бы их назвать уравнениями движения. Чаще всего это именно уравнения движения. Но есть одно исключение -- это термодинамика. В ней нет уравнений изменения состояния во времени, а уравнения связи состояний -- есть. Уравнения связи состояний образуют структурообразующее ядро теории. Мы рассмотрим три основные структурные компоненты теории. Но этого недостаточно. Необходимым, совершенно обязательным является еще один компонент -- правила интерпретации -- правила, при помощи которых мы ставим в соответствие теоретическим объектам и следствиям из теории элементы реальности, эмпирические данные. Очень часто эти правила интерпретации мы называем также физическим смыслом. Если таких правил интерпретации нет, то мы имеем дело в лучшем случае с математической теорией (вроде фредгольмовой теории интегральных уравнений), а в худшем -- с какой-нибудь игрой -- ``игрой в бисер'' или игрой в шахматы. В шахматах тоже есть теоретические объекты -- пешки, короли, "королевы", слоны, кони, есть правила оперирования, но нет интерпретации. Короли ничем не управляют, а конями, по выражению Высоцкого, ``закусить нельзя". Правила интерпретации необходимы, чтобы теория имела эмпирическое содержание. Следует заметить, что в философии науки правилам интерпретации не уделялось должного внимания. Обычно о необходимости правил интерпретации писали не философы науки, а сами ученые -- Дирак, Макс Борн, Планк. Некоторым исключением является позитивизм (правильнее -- неопозитивизм). Однако, и в работах неопозитивистов этот вопрос рассматривался очень односторонне в силу специфической особенности позитивистской позиции -- ее резкого феноменализма. И, хотя в логическом аспекте неопозитивизм получил ценные результаты, но значительно более содержательными были работы самих ученых. И все же, я повторяю, вопрос исследован далеко недостаточно. Неясно, например, обладает ли каждая теория своими собственными правилами интерпретации, резко отличными от правил других теорий, или в правилах интерпретации разных теорий есть что-то общее. С моей точки зрения вторая позиция предпочтительнее. Но этот вопрос требует специального анализа, которого я не проводил. Очень важным является то обстоятельство, что отсутствие хорошо развитой системы правил интерпретации является серьезным препятствием на пути развития теории. Рассмотрим ситуацию начального периода квантовой механики. Когда Шредингер получил свое уравнение, то естественно немедленно встал вопрос об интерпретации Но уравнение Шредингера не имеет солитонных решений и волновой пакет, которым по мнению Шредингера являлась частица, очень быстро расплывался в силу дисперсии. Но это, пожалуй, не самое страшное. Может быть можно и подобрать такой закон дисперсии, чтобы как-то блокировать такое расплывание. Мне известны такие попытки. Более существенным является другое обстоятельство. Если волны (волновой пакет) падает на некоторую потенциальную границу (барьер), то появляются две волны -- прошедшая и отраженная. По интерпретации Шредингера это должно было бы означать, что частица поделилась на две части. Но частица никогда не делится ни на какие части. Таким образом, сложилась ситуация: мы имеем уравнение Шредингера, мы можем его решать (точно или приближенно). В статических случаях мы обычно имеем задачу на собственные значения. Эти собственные значения были интерпретированы как дискретные значения физических величин -- энергии, импульса, момента и давали правильные спектры. Но что можно было сделать с функцией являющейся решением -- И только когда Макс Борн предложил вероятностную интерпретацию стало ясно, что расходящаяся волна описывает угловое распределение рассеянных частиц, и стало возможно решать задачи теории рассеяния. Отсюда ясно видно, какую важную роль играют правила интерпретации в развитии теории. Вообще-то, исторически можно объяснить не очень хорошую разработанность методологической проблематики правил интерпретации. В первой разработанной теории -- классической механики правила интерпретации казались понятными практически-интуитивно. Все мы знаем из своего опыта, что такое скорость, сила, вес, немного похуже, но представляем себе ускорение -- что еще надо? Уже в электродинамике было сложнее. И я напомню, что эфирная -- более или менее наглядная интерпретация долго не сдавала своих позиций перед интерпретацией электромагнитного поля как самостоятельной сущности. В квантовой механике стало еще сложнее. Споры по проблеме интерпретации квантовой механики ведутся еще и сейчас, и весьма активно. Но это рассматривается как ``внутреннее дело'' самой квантовой механики, а общие аспекты проблемы правил интерпретации как-то остаются за пределами рассмотрения. Но я думаю, что после нашего анализа вам стало еще более понятно, что здесь не все тривиально и есть достаточно интересное поле для дальнейшей философско-методологической разработки. Итак, мы выделили четыре основных структурных компонента любой теории система теоретических объектов математический аппарат связи между теоретическими объектами система правил интерпретации. Кроме этих фундаментальных структурных компонентов, в теории присутствуют и некоторые дополнительные. Они не столь существенны и не являются структурообразующими, но об их присутствии не мешает помнить. Во-первых, это различные упрощения, имеющие место практически во всех теориях. Так, в механике таким упрощением является представление о материальных точках, не имеющих размера. Обычно, эти упрощения носят характер ``предположений малости". Но, в принципе, возможны и другие упрощения. Второй тип дополнительных компонентов -- это специальные гипотезы о механизме того или иного конкретного механизма явления, не вытекающие из общего содержания теории. При этом очень важно, чтобы они не противоречили этому общему содержанию. Будучи достаточно хорошо развитыми, эти дополнительные предположения входят в структуру частных подтеорий в рамках общей теории. Примером такой ситуации является теория диэлектриков в рамках общей теории электрических явлений и физики твердого тела. Оба эти типа дополнительных компонент весьма важны для методологического анализа конкретной частной теории, но в общем понимании они все же играют второстепенную роль. Мы рассмотрели вопрос о том, что есть научная теория. Теперь перейдем к вопросу о том, каковы функции теории в научном познании.
|
||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 303; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.70.69 (0.013 с.) |


 -функцию. Математики сначала не признавали ее, и только через несколько лет в работе Соболева и Лорана Шварца была построена теория обобщенных функций, простейшим случаем которых является
-функцию. Математики сначала не признавали ее, и только через несколько лет в работе Соболева и Лорана Шварца была построена теория обобщенных функций, простейшим случаем которых является  =
= 
 = m
= m 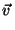 ,(или
,(или  )
)
 d
d 
 -функции, ее физическом смысле самой первой была интерпретация самого Шредингера. Он считал, что
-функции, ее физическом смысле самой первой была интерпретация самого Шредингера. Он считал, что 


