
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розрахунки страхових тарифівСодержание книги Поиск на нашем сайте Використані терміни: страховий платіж, страховий тариф, страхова сума, страхова оцінка, страхова статистика, ступінь ризику, нетто-ставка, брутто-ставка, надбавка, навантаження, актуарні розрахунки.
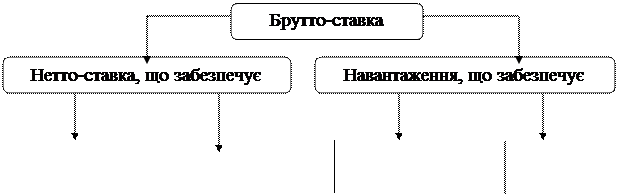
Страховик розраховує страхові тарифи, виходячи з того, що сума страхових премій, обчислених на основі тарифів, має бути такою, щоб по-перше, він міг виконувати свої зобов’язання перед страхувальниками з конкретних видів страхування (тобто зробити виплати), а по-друге – покрити витрати на утримання страхової компанії і дістати прибуток. Тому повний страховий тариф (брутто-тариф) включає в себе дві невіддільні частини: нетто-тариф і навантаження. Структуру страхового тарифу унаочнює рис. 2.15.
Рис. 2.15 Структура страхового тарифу. В загальному розумінні тарифна ставка (рис. 2.16):
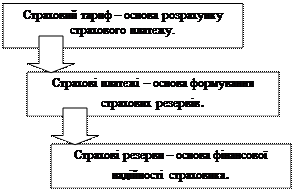
Рис. 2.16. Визначення страхового тарифу. Таким чином, з огляду на вищевказане схематично можна побудувати залежність (рис. 2.17):
Рис. 2.17. Схема наповнення страхових резервів страховика. Тарифна політика у галузі страхування повинна базуватися на таких принципах: · еквівалентності страхових відносин сторін; · доступності страхових тарифів для широкого кола страхувальників; · сталості розмірів тарифної ставки протягом тривалого часу; · забезпечення самоокупності та рентабельності страхових операцій. При розрахунку тарифів спочатку обчислюється нетто-тариф. Саме він забезпечує формування страхових резервів для виконання страховиком своїх функцій. Тому рівень нетто-тарифу має бути визначений якомога точніше. У розрахунках страхових тарифів застосовуються такі методи: · на основі теорії ймовірності та методів математичної статистики з використанням часових рядів; · на базі експертних оцінок; · за аналогією до інших об’єктів або компаній; · з використанням математичної статистики і розрахунку доходності. Після визначення нетто-тарифу обчислюється навантаження. Структура страхового тарифу з погляду співвідношення між нетто-тарифом і навантаженням не однакова для різних видів страхування. Існують “дорожчі”і “дешевші” види страхування залежно від того, скільки коштів витрачає страховик на укладення договорів страхування і їх обслуговування. Якщо нетто-тариф обчислюється спеціалістами (актуаріями) з використанням математичних методів на базі теорії ймовірності (це характерно у особистому страхуванні), то навантаження визначається емпіричним шляхом, з урахуванням фактичних розмірів витрат на ведення справ, що склалися за попередній період. З добровільних видів страхування структуру тарифної ставки визначає сам страховик і характерним, особливо для українських страхових компаній, є завищення страхових тарифів. Причому це робиться з метою отримання більшого прибутку та неорганізованості витрат на ведення справи. Тарифи, як правило, формуються вищі за середні, що склалися у конкретному виді страхування. Це порушує принцип еквівалентності у взаємовідносинах страховика і страхувальника, де страхувальник переплачує за страхування, що призводить до того, що страховики втрачають клієнтів, оскільки потенційні страхувальники не хочуть платити занадто високу ціну за той вид страхування, який в іншій країні коштує дешевше (наприклад: страхування вантажу). Таке становище склалось і тому, що українському страховику, згідно з законом України “Про страхування”: заборонено використовувати дві його головні функції розпорядження грошовими засобами: на превентивні роботи (по зменшенню, локалізації чи виключення дії страхового ризику) та інвестиційні вкладення в довгострокові прибуткові проекти. А таке приводило б до покриття витрат на ведення справи та отримання прибутку за рахунок надходжень від такої діяльності – від інвестиційних вкладень та зменшень сум по відшкодуванню збитків від прояву страхових ризиків, як це робиться у страховиків на Заході. Отже, страхові тарифи, як і ціни на будь-які інші товари, послуги, регулюються попитом і пропозицією. Але слід відзначити, що використання демпінгових тарифів, особливо нижчих, ніж ставка нетто-тарифу, вкрай небезпечно з огляду позбавлення страховій компанії можливостей сформувати адекватні страхові резерви. Тобто нагромадити об’єктивно необхідні кошти для виконання своїх зобов’язань перед страхувальниками. Через те (в тому числі), органи нагляду за страховою діяльністю ретельно контролюють рівень страхових тарифів з метою недопущення краху фінансового стану страхової компанії, її платоспроможності. Під час проведення обов’язкових видів страхування державою встановлюються граничні нормативи нетто-ставок та ставок навантаження по видах страхування. Наприклад, норматив витрат на ведення страхової справи не повинен перевищувати: · з обов’язкового державного страхування – 6% розміру брутто-тарифу; · з обов’язкового особистого страхування – 15% розміру брутто-тарифу; · з обов’язкового страхування майна та відповідальності – 20% розміру брутто-тарифу. І, як вже говорилось вище, такими ж нормативами визначаються допустимі розміри страхових сум, страхових тарифів (брутто-тарифів), страхових платежів, а також перелік об’єктів, які підлягають страхуванню, порядок сплачення страхової премії, строку дії договору страхування і т. ін. Ці обмеження покликані стримати підвищення цін на страхові послуги хоча б у сфері обов’язкового страхування. В актуарній практиці використовуються найрізноманітніші методи обчислення тарифних ставок. Але всі вони, як вже наголошувалось, повинні базуються на принципі еквівалентності фінансових зобов’язань страхувальника і страховика. Надамо деякі, найпоширеніші, підходи до трактування принципу еквівалентності та їх математичні вирази: · еквівалентність фінансових зобов’язань як еквівалентність очікуваних значень. При цьому підході зобов’язання страхувальників полягають у сплаті страхових премій, а зобов’язання страховика – в оплаті позовів страхувальника (виплати страхових сум чи сум страхових відшкодувань). Справедливою платою за ризик тут є очікуване значення випадкової величини М, тобто: р = М [ Y ], (4) де: р – величина зібраних страхових премій; Y – величина сумарних виплат страховика. · еквівалентність зобов’язань з погляду теорії розорення. При цьому підході, зобов’язання страхувальників мають безперечний характер (отримуючи поліс, страхувальник більшою мірою звільняє себе від ризику несподіваних витрат). Зобов’язання страховика, навпаки, стають непередбачувані. Тобто тепер його ризик (його виплати) будуть значно більшими за М [ Y ]. Тому страховик вимагає додаткову плату за можливість збитку – ризикову надбавку L. У зв’язку з цим залежність (4) буде такою: р = М [ Y ] + L. (5) Зразу ж постає питання: якими мають бути величини ризикової надбавки L та страхової премії? Звернемось до теорії розорення. Факт розорення будь-якої організації, в тому числі і страховика, описується співвідношенням: U + p < Y, (6) де: U – величина власних коштів страховика. Імовірність розорення із цього буде дорівнювати Р (U + р < Y). Досягнення ймовірності розорення настане, коли буде отримано величину страховими преміями Р, які задовольняли б співвідношення:
· еквівалентність зобов’язань з погляду теорії корисності. Основним критерієм цієї теорії є функція корисності U (x), що має такі властивості: n функція U зростаюча – U (x) > U (y) при х > y; n функція U задовольняє нерівність Єнсона М [ U (x)] n функція U задовольняє умову нульової корисності U (0) = 0 Взагалі сутність такої функції у мірі важливості для страховика певних грошових сум. І тому принцип еквівалентності за допомогою такої функції корисності можна записати таким чином: М [ U (U + p – Y)] = U (U). (8) Тобто, очікувана корисність капіталу страховика після прийняття ризиків не повинна зменшитися порівняно з корисністю початкового капіталу. На практиці часто застосовують експоненціальну та квадратичну функції корисно ті, вирази яких відповідно такі: U (x) = 1 – U (x) = ax – У цьому (в разі практичного застосування принципу еквівалентності в термінах теорії корисності) головна проблема – відшукання адекватної функції корисності. Але, як вже відзначалось, страхування виникає там, де існують явища і процеси випадкової природи (“чисті” ризики, які передбачають збиток). З математичного погляду випадкова величина – це змінна, яка може набувати певних значень із певною ймовірністю. У математиці таке описується функцією випадкової величини
де:
х – максимальне значення випадкової величини. Функція
Якщо х < y, то
тоді:
де: а і в – теж деякі значення випадкової величини, відмінні від величини Серед випадкових величин при цьому можна виокремити два основні типи – дискретні та абсолютно неперервні (монотонні). Дискретні – набувають скінченої (або зліченної) множини значень (наприклад, кількість позовів, страхових випадків, страхових договорів і тому подібне за визначений строк). Абсолютно неперервні – якщо функцію розподілу F
де: Абсолютно неперервними (монотонними) можна вважати, наприклад, величину майбутніх прибутків страховика або тривалість очікування між двома послідовними страховими випадками і подіями. У страховій практиці, як правило, цікавлять не самі випадкові величини, а деякі їх числові макрохарактеристики, найважливішими з них є математичне сподівання, дисперсія та їх незалежність. Математичне сподівання (середнє, очікуване) – це середньозважене за ймовірністю значення випадкової величини. Дисперсія характеризує відхилення випадкової величини від її середнього значення. Незалежність випадкових величин є добутком різних імовірностей розкриття цих подій. Наприклад, якщо при будь-яких значеннях а та b у випадках величин
Якщо випадкові величини не задовольняють наведену умову, то вони називаються залежними. Прикладом залежних випадкових величин є кількість позовів та сумарна величина виплат. Незалежними випадковими величинами можуть вважатись кількість позовів з різних видів страхування. Для дискретних випадкових величин математичне сподівання обчислюється за формулою:
де:
Для абсолютно неперервних випадкових величин математичне сподівання (очікування) має вигляд:
де: Коли випадкова величина невід’ємна, тобто:
Для будь-яких сталих а, b та випадкових величин М [ a ] = a; (20)
А дисперсія випадкової величини, як відхилення від її середнього значення обчислюється як математичне сподівання квадрата відхилення цієї величини від її математичного сподівання:
Дисперсія задовольняє такі співвідношення:
Д [ a ] = 0; (25) Д [ b Д [ де: а, b – довільні сталі;
Якщо випадкова величина невід’ємна, то дисперсію можна обчислити за формулою:
Поряд з дисперсією часто використовують похідні поняття – стандартне відхилення та коефіцієнт варіації. Стандартне (середньоквадратичне) відхилення це корінь із дисперсії:
Коефіцієнт варіації – відношення стандартного відхилення випадкової величини до модуля математичного сподівання:
Часто ми не маємо інформації про реальний розподіл випадкової величини Вибіркове середнє використовують для оцінювання математичного сподівання:
Незсунена вибіркова дисперсія є оцінкою дисперсії випадкової величини:
Відповідно величини вибіркової (емпіричної середньої та незсуненої вибіркової) емпіричної дисперсії розраховують такими залежностями:
Класичний підхід визначення тарифів можна розглянути на прикладах договорів загального страхування, які не є договорами страхування життя. Договори загального страхування характеризуються відносно коротким строком дії договору - від кількох днів до одного року (вантажоперевезення, транспортне страхування, страхування споруд, будівель тощо). Ця особливість визначає характери-особливості розрахунку страхових тарифів за такими договорами: · вираховується величина лише разової страхової премії; · не враховується можливий інвестиційний прибуток від розміщення тимчасово вільних коштів страхових резервів із цих видів страхування. Наприклад, тарифи будівельних ризиків, наведені в додатках №1 та №2, можуть бути розраховані за схемою договорів загального страхування. При розрахунку нетто-премії вважають, що величина N разової нетто-премії виражає еквівалентність зобов'язань страховика та страхувальників і пропорційна величині S страхової суми: N = Т S, (35) де: коефіцієнт Т називають нетто-тарифом чи нетто-ставкою. Брутто-премія В, або просто страхова премія, пропорційна нетто-премії N:
де:
Для визначення нетто-тарифу за договором загального страхування розглянемо гіпотетичний випадок, коли відома вся необхідна для розрахунків інформація. Припустимо, що під час проведення страхування визначеного ризику (наприклад, майнове страхування будівель від стихійного лиха) протягом фіксованого проміжку часу · проведення страхування за п (п = 1,2,...) договорами із страховими сумами · настання за цими договорами страхових випадків із страховими виплатами Визначимо розмір нетто-тарифу під час страхування ризику, який відповідав би взятим зобов'язанням страховика з названих видів страхування. У розглянутому випадку нетто-тариф можна визначити на підставі загального принципу еквівалентності зобов'язань страховика та страхувальників. Зобов'язання страховика дорівнюють сумі страхових відшкодувань:
а зобов'язання страхувальників - сумі внесених нетто-премій:
де:
або:
У цьому балансовому співвідношенні зручно виконати усереднення за договорами страхування, поділивши обидві частини на mn:
А далі, ввівши значення
перейти до співвідношення:
звідки знаходимо шукане значення нетто-тарифу:
Останню рівність записують, як правило, у вигляді:
тобто виражають нетто-тариф під час страхування визначеного ризику через два основні параметри: 1) коефіцієнт збитковості за цим страховим ризиком Кзб:
2) відносну частоту настання страхової події за цим страховим ризиком v:
Наведені співвідношення вирішують поставлене завдання і дозволяють розрахувати нетто-тариф під час страхування визначеного ризику лише у апостеріорному (післядослідному) випадку, коли відома вся необхідна інформація, а саме відомі значення параметрів При апріорному визначенні нетто-тарифу у загальному випадку розглянутої моделі страхових відшкодувань у співвідношенні Для розв'язання цієї суперечності широкого застосування набув метод, який ґрунтується на тому, що замість випадкової величини достатньо взяти її найбільше можливе із заданою довірчою ймовірністю значення. Такий підхід визначає структуру нетто-тарифу за договором загального страхування:
де:
де: За законом великих чисел при великих значеннях п випадкова величина
Величини страхових виплат
Останні співвідношення дозволяють спростити формулу обчислення величини
Практично на страхування беруть ризики, ймовірність настання яких не вища за 0.25, тобто при р
Отже, нетто-тариф під час страхування виділеного ризику розраховується із заданою довірчою ймовірністю
де: п - кількість договорів страхування за визначеним ризиком, що планується; р - ймовірність настання страхової події за визначеним ризиком; М [ Кзб ] - математичне сподівання величини Кзб для визначеного ризику практично не змінюється і має слідуючи значення: • 0.3 - при страхуванні від нещасних випадків та хвороби; • 0.4 - при страхуванні засобів наземного транспорту; • 0.5 - при страхуванні вантажів та майна (крім засобів транспорту); • 0.6 – при страхуванні засобів повітряного та водного транспорту; • 0.7 – при страхуванні відповідальності власників автотранспортних засобів та інших видів відповідальності, а також при страхуванні фінансових ризиків. Для обчислення нетто-премії N за договором страхування визначеного ризику слід нетто-тариф Т помножити на величину S страхової суми (залежність 35): N = S • T. (56) Зауважимо, що величина нетто-тарифу істотно залежить: • від запланованої кількості договорів страхування за визначеним ризиком і зменшується з їх зростанням до математичного сподівання величини збитків страхової суми; • від значення довірчої ймовірності шуканого тарифу і зростає з наближенням цього значення до одиниці; • від точності вибору значення коефіцієнта збитковості. Розрахунки страхових тарифів в індивідуальній моделі ризику. Наведені формули виражають класичний підхід розрахунку нетто-тарифу для страхового ризику за наявності мінімальної інформації про можливі майбутні страхові виплати. Якщо відомі додаткові статистичні дані про процес настання страхової події, можливе застосування більш точних методів обчислення страхових тарифів. Для розв'язання відповідних задач вводять різні статистичні моделі страхових ризиків і розглядають відповідні моделі розподілу сумарного розміру страхового відшкодування. Найпростішою з них є модель індивідуальних ризиків, яка щодо договору страхування передбачає таке: • для кожного договору страхування відомі статистичні властивості пов’язаного з ним можливого відшкодування Зауважимо, що далеко не за кожним договором виплачується страхове відшкодування, тому деякі випадкові величини
У загальному випадку при використанні моделі індивідуального ризику величина умови достатності із заданою довірчою ймовірністю отриманих страхових премій для виконання зобов'язань страховика за формулою:
де:
Основний внесок до величини На практиці використовують кілька способів розрахунку відносної страхової надбавки під час страхування визначеного ризику: 1) з фіксованим значенням для всіх договорів страхування:
де:
2) зі змінним значенням, пропорційним дисперсії або середньоквадратичному відхиленню величини страхового відшкодування
або:
Числові характеристики випадкових величин М [ У разі, коли відомі числові характеристики сумарного розподілу
або ймовірності розорення (недостатності наявних страхових резервів):
де: Розрахунок страхових тарифів у колективній моделі ризику. Складнішу модель розподілу сумарного розміру страхового відшкодування за визначеним ризиком виражає колективна модель ризику, яка розглядає не окремі договори страхування, а весь портфель договорів за даним страховим ризиком і передбачає таке: · кількість вимог про страхове відшкодування за даним ризиком на фіксованому проміжку часу є випадкова величина (як правило, з Пуассонівським розподілом); · значення послідовних страхових відшкодувань · випадкові величини Колективна модель враховує можливість неодноразового настання страхової події за одним договором страхування (що дуже важливо в договорах загального страхування), не обмежена умовою визначеності кількості майбутніх договорів страхування та розглядає завжди додатні значення відшкодувань
За заданими числовими характеристиками кількості
Найпростішу та найпоширенішу модель розподілу кількості страхових вимог
причому: У цьому випадку розподіл випадкової величини S називають складним розподілом Пуассона, а її числові характеристики визначають за формулами:
Параметри У страховій практиці важливим є той факт, що сума незалежних випадкових величин, кожна з яких має складний розподіл Пуассона з параметрами
за умови, що ряд
Наведене твердження на практиці використовують у таких випадках: · при об’єднанні m страхових портфелів, таких що сумарний розмір страхових відшкодувань
· при дослідженні сумарного за m років страхового відшкодування S за одним і тим самим страховим ризиком з незалежними річними сумарними страховими відшкодуваннями При використанні моделі колективного ризику величина В страхової премії для всіх договорів страхування однакова і визначається з умови достатності із заданою довірчою ймовірністю отриманих страхових премій для виконання зобов’язань страховика за формулою:
де: М [ Y ] - математичне сподівання виплати одного страхового відшкодування;
Основний внесок до величини В у загальному випадку Відносна страхова надбавка при страхуванні визначеного ризику має фіксоване для всіх договорів значення і розраховуєть
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 326; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.012 с.) |




 Страховий фонд
Страховий фонд

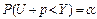 . (7)
. (7)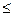 U (M [ x ]);
U (M [ x ]);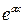 , (9)
, (9)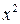 . (10)
. (10)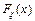 :
: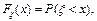 (11)
(11)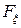 (х) – інтегральна функція випадкової величини;
(х) – інтегральна функція випадкової величини; – значення випадкової величини;
– значення випадкової величини; ; (12)
; (12)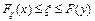 , де у – деяке значення, відмінне від значення х.
, де у – деяке значення, відмінне від значення х.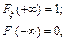 (13)
(13)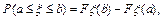 (14)
(14)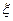 .
. (15)
(15) – деяка невід’ємна функція яка показує щільність розподілу випадкової величини
– деяка невід’ємна функція яка показує щільність розподілу випадкової величини  .
.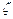 ймовірність подій Р (
ймовірність подій Р (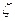 < b) буде добутком цих подій
< b) буде добутком цих подій  та
та 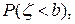 -- тобто:
-- тобто: (16)
(16)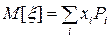 , (17)
, (17)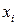 - значення, яких набуває випадкова величина;
- значення, яких набуває випадкова величина;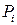 - імовірність реалізації випадкових величин.
- імовірність реалізації випадкових величин. (18)
(18)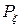 - щільність випадкової величини
- щільність випадкової величини  , математичне сподівання можна обчислити за формулою:
, математичне сподівання можна обчислити за формулою: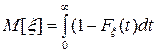 .
.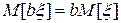 ; (21)
; (21)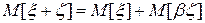 ; (22)
; (22)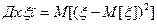 . (23)
. (23) ; (24)
; (24)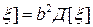 ; (26)
; (26)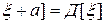 ; (27)
; (27)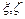 -- випадкові величини.
-- випадкові величини.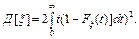 . (28)
. (28)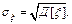 . (29)
. (29) . (30)
. (30)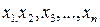 . Ця сукупність значень називається вибірковою (середньою чи незсуненою) дисперсією.
. Ця сукупність значень називається вибірковою (середньою чи незсуненою) дисперсією. . (31)
. (31)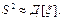 . (32)
. (32) (33)
(33)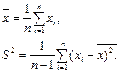 (34)
(34) (36)
(36)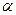 коефіцієнт пропорційності (
коефіцієнт пропорційності ( , (37)
, (37) (наприклад, одного року) страховиком заплановано:
(наприклад, одного року) страховиком заплановано: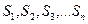 відповідно;
відповідно;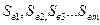 .
. (38)
(38)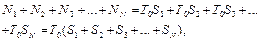 (39)
(39)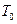 - нетто-тариф, який потрібно визначити. Значення
- нетто-тариф, який потрібно визначити. Значення  (40)
(40)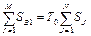 (41)
(41)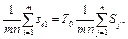 . (42)
. (42) - середньої страхової виплати та значення
- середньої страхової виплати та значення 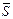 -- середньої страхової суми на один договір:
-- середньої страхової суми на один договір: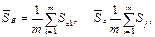
 (44)
(44)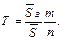 (45)
(45)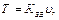 , (46)
, (46) (47)
(47) (48)
(48) або
або  На практиці при апріорному (до початку досліду) визначенні тарифів жодний із цих параметрів невідомий, і всі вони є випадковими додатніми величинами. Але наведений приклад та отримані співвідношення мають важливе значення для перевірки і коригування значень тарифів за результатами страхової діяльності, правильності апріорного визначення тарифів. Саме ці співвідношення вказують на необхідність у діяльності кожної страхової компанії постійного спостереження та аналізу значень параметрів
На практиці при апріорному (до початку досліду) визначенні тарифів жодний із цих параметрів невідомий, і всі вони є випадковими додатніми величинами. Але наведений приклад та отримані співвідношення мають важливе значення для перевірки і коригування значень тарифів за результатами страхової діяльності, правильності апріорного визначення тарифів. Саме ці співвідношення вказують на необхідність у діяльності кожної страхової компанії постійного спостереження та аналізу значень параметрів  за прийнятим на страхування ризиком і дозволяють періодично коригувати наперед визначені для такого ризику тарифні ставки.
за прийнятим на страхування ризиком і дозволяють періодично коригувати наперед визначені для такого ризику тарифні ставки. потрібно розв'язати суперечність, яка полягає в тому, що ліва частина (нетто-тариф) має бути наперед визначеною фіксованою величиною, а права частина є випадкова величина, значення якої можуть істотно змінюватися в різні періоди діяльності страховика.
потрібно розв'язати суперечність, яка полягає в тому, що ліва частина (нетто-тариф) має бути наперед визначеною фіксованою величиною, а права частина є випадкова величина, значення якої можуть істотно змінюватися в різні періоди діяльності страховика.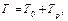 (49)
(49)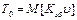 - основна частина нетто-тарифу (математичне сподівання збитків з одиниці страхової суми в разі великої кількості страхування за визначеним ризиком);
- основна частина нетто-тарифу (математичне сподівання збитків з одиниці страхової суми в разі великої кількості страхування за визначеним ризиком);
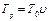 -- ризикова (страхова) надбавка до основної частини нетто-тарифу, яка із заданою довірчою ймовірністю враховує можливі небажані відхилення відносної величини виплат і обчислюється за формулою:
-- ризикова (страхова) надбавка до основної частини нетто-тарифу, яка із заданою довірчою ймовірністю враховує можливі небажані відхилення відносної величини виплат і обчислюється за формулою: (50)
(50)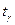 - квантиль рівня
- квантиль рівня 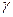 нормального розподілу.
нормального розподілу.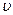 прямує з ймовірністю одиниці до значення р теоретичної ймовірності настання страхової події за визначеним ризиком та розподілена за нормальним законом з параметрами:
прямує з ймовірністю одиниці до значення р теоретичної ймовірності настання страхової події за визначеним ризиком та розподілена за нормальним законом з параметрами: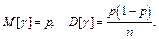 (51)
(51)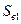 будемо вважати розподіленими за рівномірним законом. Таким чином, для коефіцієнта збитковості
будемо вважати розподіленими за рівномірним законом. Таким чином, для коефіцієнта збитковості  маємо:
маємо: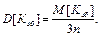 (52)
(52) :
: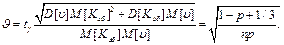 (53)
(53)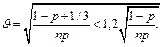 (54)
(54)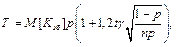 , (55)
, (55) , де: k - порядковий номер договору.
, де: k - порядковий номер договору. (страхові відшкодування за ітим договором) можуть дорівнювати нулю. Загальний розмір страхового відшкодування за страховою подією, тобто розмір зобов'язань страховика, визначає між собою сума випадкових величин:
(страхові відшкодування за ітим договором) можуть дорівнювати нулю. Загальний розмір страхового відшкодування за страховою подією, тобто розмір зобов'язань страховика, визначає між собою сума випадкових величин: (57)
(57)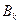 страхової премії за k-м договором страхування розраховується з
страхової премії за k-м договором страхування розраховується з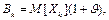 (58)
(58)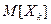 - математичне сподівання відшкодувань за k-м договором страхування;
- математичне сподівання відшкодувань за k-м договором страхування;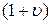 , (тобто ризикова, або страхова надбавка до основної частини) - враховує можливі небажані відхилення відносної частоти настання страхової події.
, (тобто ризикова, або страхова надбавка до основної частини) - враховує можливі небажані відхилення відносної частоти настання страхової події.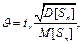 (59)
(59) - математичне сподівання сумарного розміру страхових відшкодувань;
- математичне сподівання сумарного розміру страхових відшкодувань; - дисперсія сумарного розміру страхових відшкодувань;
- дисперсія сумарного розміру страхових відшкодувань;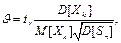 (60)
(60)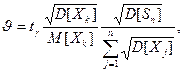 k =1,2,..., n. (61)
k =1,2,..., n. (61) страхових відшкодувань за страховим ризиком на підставі центральної граничної теореми можна обчислити ймовірність достатності наявних страхових резервів розміру
страхових відшкодувань за страховим ризиком на підставі центральної граничної теореми можна обчислити ймовірність достатності наявних страхових резервів розміру  (62)
(62)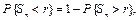 (63)
(63)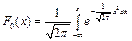 -- інтегральна функція нормованого нормального розподілу.
-- інтегральна функція нормованого нормального розподілу.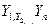 за портфелем страхового ризику за цей проміжок часу утворюють послідовність випадкових величин, які однаково розподілені;
за портфелем страхового ризику за цей проміжок часу утворюють послідовність випадкових величин, які однаково розподілені;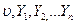 незалежні в сукупності.
незалежні в сукупності.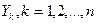 (на відміну від індивідуальної моделі, де значення відшкодувань
(на відміну від індивідуальної моделі, де значення відшкодувань  (64)
(64)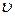 вимог про страхове відшкодування та величиною Y одного відшкодування залежно від загального випадку можемо знайти числові характеристики сумарного розміру S страхових відшкодувань за страховим ризиком у колективній моделі:
вимог про страхове відшкодування та величиною Y одного відшкодування залежно від загального випадку можемо знайти числові характеристики сумарного розміру S страхових відшкодувань за страховим ризиком у колективній моделі: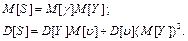 (66)
(66)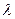 , коли:
, коли: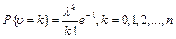 (67)
(67) . (68)
. (68)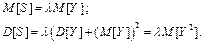 (70)
(70)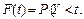 розподілу величини значень
розподілу величини значень  також має складний розподіл Пуассона з параметрами:
також має складний розподіл Пуассона з параметрами: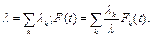 (71)
(71) - збіжний.
- збіжний.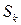 , k = 1,2,…, m по кожному з них має складний розподіл Пуассона з параметрами
, k = 1,2,…, m по кожному з них має складний розподіл Пуассона з параметрами  внаслідок отримують об’єднаний портфель, сумарний розмір страхових відшкодувань S якого буде визначати складний розподіл Пуассона з параметрами:
внаслідок отримують об’єднаний портфель, сумарний розмір страхових відшкодувань S якого буде визначати складний розподіл Пуассона з параметрами: ; (72)
; (72) , k = 1,2,…, m, кожне з яких має складний розподіл Пуассона, можемо вважати, що злежність (72) має також складний розподіл Пуассона.
, k = 1,2,…, m, кожне з яких має складний розподіл Пуассона, можемо вважати, що злежність (72) має також складний розподіл Пуассона.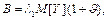 (73)
(73)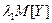 називають основною частиною нетто-премії, а
називають основною частиною нетто-премії, а  називають ризиковою (страховою) надбавкою до основної частини, яка із заданою довірчою ймовірністю враховує можливі небажані відхилення відносної частоти настання страхової події.
називають ризиковою (страховою) надбавкою до основної частини, яка із заданою довірчою ймовірністю враховує можливі небажані відхилення відносної частоти настання страхової події.


