
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сил (или диаграмм ускоряющих и замедляющих усилий).Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Диаграммы удельных равнодействующих сил (или диаграммы ускоряющих и замедляющих усилий) – зависимости равнодействующей силы от скорости движения поезда по площадке, т. е. сопротивление от кривой и от уклона не зависит от скорости, поэтому учитывается дополнительно. Заполняем столбец 12 табл. №1 значениями полной силы тяги, которая берется из ПТР ([1], рис.4.9, стр.104). Заполняем столбец 13 табл.№1 значениями удельной силы тяги, которая вычисляется по формуле:
где Fk и ¦k – соответственно полная и удельная силы тяги, P и Q – вес локомотива и состава грузового поезда.
Заполняем столбец 14 табл. №1 значениями удельной равнодействующей силы тяги и силы сопротивления, т.е. их разностью: ¦K - w0. Заполняем столбец 16 табл. №1 значениями коэффициента трения колодки о колесо, который вычисляется по формуле ([1], формула 59, стр.11):
где jкр – расчетный коэффициент трения колодки о колесо (для стандартных чугунных колодок и колодок с повышенным содержанием фосфора); V – скорость движения поезда. Расчетный коэффициент трения вводится для того, чтобы не вводить в расчет зависимость коэффициента трения от силы нажатия на колодку, т.е. зависимость jк=¦(k,V). Расчетным тормозным коэффициентом поезда Jр является отношение суммы тормозных расчетных сил нажатия всех тормозных колодок поезда к массе поезда
где αтi – коэффициент торможения вагонов (=1); i – количество осей вагона; qi – вес вагонов брутто; gi – процентное содержание вагонов в %, Кр=7×т×с
Расчетный тормозной коэффициент – это важный эксплуатационный показатель, характеризующий степень вооруженности поезда тормозными средствами. Расчетный тормозной коэффициент показывает, какое тормозное нажатие (в силах расчетного нажатия) приходится на единицу веса состава (или на 100 тс веса состава как принято в тяговых расчетах для поездной работы). Значение Jp подставляем в столбец 15 табл. №1 и для всех значений скорости V оно будет постоянное. При определении расчетного тормозного коэффициента, тормозные средства локомотива и его вес в расчет не вводятся. Тормозная сила bT определяется по формуле 2.40 ([2], (стр.57); bT = 1000·åKр×jkр (4.4) Если расчетный коэффициент трения не зависит от силы нажатия (так принимается при расчете тормозной силы по методу приведения), его можно вынести за знак суммирования ([1], формула 55, стр. 11):
bT = 1000×jkр×åKр (4.5)
Переходя к удельной тормозной силе, получим:
где Тормозные силы служат для уменьшения скорости движения поезда до его полной остановки или до заданной скорости. На затяжных спусках используется регулировочное торможение, при помощи которого поддерживается заданная скорость. Для всех значений скоростей заполняем столбец 17 значениями удельной тормозной силы при экстренном торможении (α=1). В режиме торможения удельная равнодействующая сила будет равна Заполняем столбец 18 значениями удельной равнодействующей силой При построении диаграммы удельных равнодействующих сил принято откладывать влево от начала координат положительные удельные равнодействующие силы, то есть такие, которые направлены по ходу движения поезда, а вправо – отрицательные, то есть направленные в противоположную движению поезда сторону. Диаграмма Диаграммы Диаграммы удельных равнодействующих сил позволяют определить величину и знак равнодействующей при любой скорости и любом режиме движения на площадке или при любом уклоне. При движении по уклону в режиме тяги удельная равнодействующая сила равна
Следовательно, при любой скорости и режиме движения удельная равнодействующая сила на уклоне отличается от удельной равнодействующей силы для случая движения по площадке на величину, численно равную крутизне уклона. Таким образом, диаграммами удельных равнодействующих сил (см.приложение 1) можно пользоваться для условий движения по любому уклону. Для этого необходимо перевести начало координат диаграммы влево (в случае подъёма) или вправо (в случае спуска) на число единиц удельной равнодействующей силы, равное числу тысячных подъёма или спуска.
Таблица №1
Спрямление профиля пути
Для учёта влияния кривых и уклонов пути на сопротивление движению поезда при расчёте массы состава, определении скорости движения и времени хода поезда необходимо спрямлять продольный профиль пути и план пути. При этом кривые в плане пути заменять фиктивными подъёмами в пределах спрямлённых элементов. Спрямлять разрешается только близкие по значению уклона элементы профиля одного знака. Элементы профиля на раздельных пунктах с прилегающими элементами профиля перегонов не спрямляются. Уклон спрямлённого участка определяется по формуле
где
Кривые заменяют фиктивными подъёмами, крутизна которых определяется по формуле
где
Проверка возможности спрямления производится для каждого элемента действительного профиля, входящего в спрямляемый участок по формуле
где
Приведённый уклон будет равен:
Спрямление профиля
Таблица №2
Решение тормозной задачи
При расчётах тормозных путей поездов полный тормозной путь
где
Действительный тормозной путь вычисляется в результате суммирования тормозных путей, определяемых по интервалам скорости, при условии постоянства величин тормозной силы, удельного сопротивления движению и уклона в принятом интервале скоростей
где
Так как число осей поезда m=29·4+3·8=140 < 200, то время подготовки автотормозов к действию определяется по формуле ([1], ф.68, стр.18):
Тормозной путь
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 651; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.25.139 (0.008 с.) |

 (4.1)
(4.1)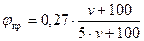 (4.2)
(4.2) (4.3)
(4.3)
 (4.7)
(4.7) – удельная тормозная сила.
– удельная тормозная сила.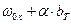 .
. при экстренном торможении (α=1) и столбец 19 – значениями удельной равнодействующей силой
при экстренном торможении (α=1) и столбец 19 – значениями удельной равнодействующей силой  при служебном торможении (α=0,5).
при служебном торможении (α=0,5). при i=0 обычно располагаются большей своей частью слева от оси скорости. С увеличением скорости значения равнодействующей уменьшаются, так как сила тяги становится меньше, а основное сопротивление возрастает. При некоторой скорости сила тяги становится равной сопротивлению движения поезда, а равнодействующая сила – нулю. При больших по сравнению с этой скоростях равнодействующая в режиме тяги становится отрицательной, то есть направленной против движения поезда.
при i=0 обычно располагаются большей своей частью слева от оси скорости. С увеличением скорости значения равнодействующей уменьшаются, так как сила тяги становится меньше, а основное сопротивление возрастает. При некоторой скорости сила тяги становится равной сопротивлению движения поезда, а равнодействующая сила – нулю. При больших по сравнению с этой скоростях равнодействующая в режиме тяги становится отрицательной, то есть направленной против движения поезда. и
и  всегда располагаются справа от оси скорости, так как эти равнодействующие силы отрицательны, то есть, направлены против движения поезда.
всегда располагаются справа от оси скорости, так как эти равнодействующие силы отрицательны, то есть, направлены против движения поезда. , где общее удельное сопротивление движению
, где общее удельное сопротивление движению  включает дополнительное удельное сопротивление от уклона
включает дополнительное удельное сопротивление от уклона  , численно равное крутизне уклона:
, численно равное крутизне уклона: (4.8)
(4.8) (5.1)
(5.1) – уклон каждого из элементов профиля, входящих в спрямляемый участок, ‰;
– уклон каждого из элементов профиля, входящих в спрямляемый участок, ‰; – длина каждого из элементов профиля, входящих в спрямляемый участок, м;
– длина каждого из элементов профиля, входящих в спрямляемый участок, м; – длина спрямляемого элемента, м.
– длина спрямляемого элемента, м. (5.2)
(5.2) – центральный угол данной кривой в пределах спрямляемого элемента, град.
– центральный угол данной кривой в пределах спрямляемого элемента, град.
 (5.3)
(5.3) – длина любого элемента действительного профиля пути, входящего в спрямлённый элемент, м;
– длина любого элемента действительного профиля пути, входящего в спрямлённый элемент, м; – абсолютная разность между уклоном спрямлённого элемента и действительным уклоном отдельного (проверяемого) элемента, ‰.
– абсолютная разность между уклоном спрямлённого элемента и действительным уклоном отдельного (проверяемого) элемента, ‰. (5.4)
(5.4) , проходимый от начала торможения до остановки, определяется как сумма подготовительного пути
, проходимый от начала торможения до остановки, определяется как сумма подготовительного пути  и действительного пути торможения
и действительного пути торможения  . Подготовительный путь подсчитывается по формуле:
. Подготовительный путь подсчитывается по формуле: (6.1)
(6.1) – скорость поезда в начальный момент торможения, км/ч;
– скорость поезда в начальный момент торможения, км/ч; – время подготовки тормозов к действию, сек.
– время подготовки тормозов к действию, сек.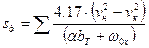 (6.2)
(6.2) ,
,  – начальная и конечные скорости поезда в принятом расчётном интервале скоростей, км/ч;
– начальная и конечные скорости поезда в принятом расчётном интервале скоростей, км/ч;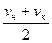 ;
; (6.3)
(6.3) ‰ равен
‰ равен  ‰ равен
‰ равен 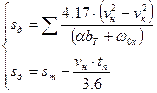 (6.4)
(6.4)


