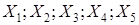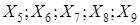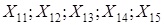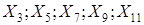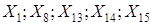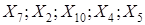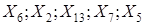Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дополнительные баллы, которые можно набрать в течение семестраСодержание книги
Поиск на нашем сайте
Критерии оценки на зачете с оценкой На зачете с оценкой магистранту предлагается билет, состоящий из одного теоретического вопроса и одного практического задания. Оценивается полнота раскрытия содержания теоретического вопроса и правильность выполнения практического задания, грамотное его оформление и наличие необходимых выводов. После ответа магистранту могут быть заданы дополнительные вопросы, как по материалам билета, так и по основным определениям курса в целом. Расчет баллов на зачете
Критерии граничных оценок за задания на зачете
V. ПЕРЕЧЕНЬ УЧЕБНО-МЕТОДИЧЕСКОГО ОБЕСПЕЧЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ ОБУЧАЮЩИХСЯ Самостоятельная работа магистрантов является ведущей формой учебной деятельности магистранта. Такое её значение определяется самим характером и особенностями образовательного процесса. Освоение человеком любого знания, формирование умений и навыков происходит всегда на индивидуальном уровне. На первом этапе организации самостоятельной работы рекомендуется проверить способности магистрантов правильно работать с литературой, пользоваться учебной и публичными библиотеками, электронно-библиотечной системой (ЭБС) вуза, электронными вариантами учебных пособий, материалами в сети Интернет. Необходимо проконсультировать магистрантов по организации компьютерного рабочего места, необходимого для прохождения курса; рекомендовать стандартные программы просмотра основных типов файлов, и программные продукты, необходимые для выполнения заданий по курсу. Далее желательно помочь магистранту в организации качественной системы коммуникационного взаимодействия с преподавателем и одногруппниками (выделить и сообщить время консультаций, создать базу электронных адресов, группу в социальных сетях и т.п.). Основная самостоятельная работа магистрантов по курсу «Эконометрика (продвинутый уровень)» заключается в выполнении контрольных и домашних работ и подготовке к лабораторным работам. При выполнении данных работ магистранты активно пользуются конспектами лекций и учебно-методическими материалами, предоставляемыми преподавателем явно или в виде ссылок на Интернет-ресурсы, учебниками из библиотеки и ЭБС, материалами сети Интернет. Магистрантам, имеющим тягу и способности к научной работе, желательно предоставлять в качестве дополнительных заданий проблемно-ориентированные задания с актуальной тематикой. Рекомендуется согласовывать такие задания с выпускающими кафедрами для возможности дальнейших исследований с подготовкой выступлений на конференциях, статей. Учебно-методическое обеспечение для самостоятельной работы обучающихся по данной дисциплине – перечень основной и дополнительной учебной литературы, необходимой для освоения дисциплины (приведен в рабочей программе ниже); – конспекты лекций (предоставляются магистрантам в электронном виде через старосту или иного ответственного магистранта и всегда могут быть выданы каждому магистранту на кафедре или по запросу по электронной почте); – методическое пособие для самостоятельной работы магистрантов по дисциплине Эконометрика (продвинутый уровень) (предоставляется в электронном виде через старосту или иного ответственного магистранта и всегда может быть выдано каждому магистранту на кафедре или по запросу по электронной почте); – задания контрольных работ магистрантам очной формы обучения (полностью приведены в ФОС); – вопросы для оценки качества освоения дисциплины (приведены ниже). Примеры задач для самостоятельной работы магистрантов Задание По данным практической работы найти зависимость между Y (в т) и величиной основных производственных фондов (ОПФ) X (в млн. руб.) для совокупности 50 однотипных предприятий, вычислить коэффициент корреляции и проверить его значимость. Оформить отчет. Задача По данным бюджетного обследования 8 случайно выбранных семей изучается зависимость накоплений
Требуется: 1. Найти коэффициенты парной корреляции. Проанализировать их. 2. Построить линейную модель множественной регрессии. 3. Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации. 4. С помощью 5. Проверить значимость найденных коэффициентов уравнения регрессии. 6. Составить уравнение линейной парной регрессии, оставив лишь один значащий фактор. Примеры задач на контрольную работу магистрантов Задача Имеются данные, отражающие динамику курса акций двух компаний А и В в одном и том же временном промежутке. Для наблюдений выбрали пять моментов времени. Компания А:
Компания В:
1) Построить уравнения регрессии курса акций Y по времени Х обеих компаний. 2) Проверить значимость коэффициентов регрессии при уровне значимости 3) Построить доверительные интервалы для значений переменной У. Если это возможно, то дать прогноз курса акций в момент времени Х=6 и Х=7 для обеих компаний. 4) Вычислив дисперсию курса акций обеих компаний, определить, что менее рискованно: купить акции компании А или компании В. 5) На основе проведённого анализа определить, какое из предложенных решений является наиболее приемлемым: а) купить акции компании А в момент времени Х=6; б) купить акции компании В в момент времени Х=6; в) не покупать акций этих двух компаний в момент времени Х=6. Ответ обосновать. Задача Используя данные лабораторной работы №4, осуществите первый шаг метода группового учёта аргументов для пяти показателей согласно Вашему варианту:
В качестве опорных функций примените зависимости вида:
Наилучшие выбранные модели протестируйте на наличие автокорреляции и гетероскедастичности. Вопросы для оценки качества освоения дисциплины 1. Сбор статистической информации 2. Описательная статистика 3. Построение экономико-математической модели 4. Временные ряды 5. Системы одновременных уравнений 6. Оценка параметров эконометрической модели 7. Метод наименьших квадратов 8. Линейная парная и множественные регрессии: смысл и оценка параметров 9. Доверительные интервалы 10. Проверка качества построенной модели 11. Коэффициент детерминации. Значимость коэффициентов уравнения регрессии 12. Применение модели в практической деятельности 13. Анализ экономических показателей 14. Прогнозирование по уравнению регрессии 15. Матричная форма модели регрессии 16. Предпосылки метода наименьших квадратов. 17. Автокорреляция остатков 18. Гомоскедастичность и гетероскедастичность 19. Ковариационная матрица возмущений 20. Частные случаи обобщённого метода наименьших квадратов 21. Гетероскедастичность остатков 22. Тест ранговой корреляции Спирмена 23. Тест Голдфельда-Квандта 24. Взвешенный метод наименьших квадратов 25. Масштабирование исходных данных 26. Методы обнаружения автокорреляции остатков 27. Критерий Дарбина-Уотсона 28. Метод рядов 29. Методы устранения проблем автокорреляции 30. Примеры использования частных случаев обобщённого метода наименьших квадратов 31. Задачи структурно-параметрической идентификации моделей 32. Параметрические и непараметрические алгоритмы метода группового учёта аргументов 33. Применение метода в макроэкономическом моделировании 34. Полиномиальные базисные функции 35. Общая связь между входными и выходными переменными 36. Ряд Вольтерра 37. Полином Колмогорова-Габора 38. Этапы реализации МГУА 39. Особенности алгоритмов МГУА и их отличие от других алгоритмов структурной идентификации 40. Спектр алгоритмов МГУА. Комбинаторный алгоритм
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 272; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.133.214 (0.009 с.) |

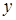 от дохода
от дохода  , расходов на питание
, расходов на питание 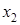 , и стоимости имущества
, и стоимости имущества 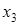 (все данные приведены в условных единицах):
(все данные приведены в условных единицах): -критерия Фишера оценить статистическую надежность уравнения регрессии и коэффициента детерминации
-критерия Фишера оценить статистическую надежность уравнения регрессии и коэффициента детерминации 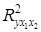 .
.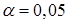 и построить доверительные интервалы с надёжностью 95%.
и построить доверительные интервалы с надёжностью 95%.