
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 5. Экономический рост, его моделирование, учет состояния экологии и социальной сферы в экономико-математических моделяхСодержание книги
Поиск на нашем сайте
Раздел 5. Экономический рост, его моделирование, учет состояния экологии и социальной сферы в экономико-математических моделях Модели экономического роста широко представлены в экономических исследованиях. На основе этих моделей решаются разнообразные задачи анализа и прогнозирования развития национальных экономик. Современные модели экономического роста учитывают возможность инвестирования не только в физический капитал, но и в ряд других производственных ресурсов. Это связано с признанием того, что росту эффективности использования производственных ресурсов способствует большое число технологических, организационных и других факторов, совокупность которых охватывается понятием научно-технологического прогресса (НТП). Кроме того, в последние годы появляется все больше работ, в которых исследуется, как рост производства отражается на экологической ситуации, как экология влияет на возможность роста, как уровень экономического развития связан с различными показателями, характеризующими состояние социальной сферы. Однако не уделяется должного внимания взаимному влиянию экономики, экологии и социальной сферы несмотря на стремление многих стран мира к устойчивому развитию, под которым понимают развитие, удовлетворяющее потребности как настоящего, так и будущего поколений в экономических и экологических благах. Это означает рост валового внутреннего продукта (ВВП) при одновременном снижении антропогенной нагрузки на окружающую среду. Понятие устойчивого развития также включает в себя проблемы сокращения разрыва в уровнях экономического развития различных стран и благосостояния их населения, безопасности и т.д. Решение данных проблем требует использования методов экономико-математического моделирования экономического роста с учетом экологического и социального факторов. Экзогенный – внешний; эндогенный – внутренний. Модель АК Эта модель была предложена Р.Лукасом, который делает попытку объяснить экономический рост без привлечения предпосылки от экзогенно задаваемый темпах роста НТП. В этой модели выпуск описывается производственной функцией Кобба-Дугласа вида:
где Инвестиции в момент t представляют собой сумму инвестиций в физический капитал Ik (t) и человеческий капитал Ih (t):
Равновесие на рынке товаров и услуг, как и в модели Солоу, описывается уравнением: Y (t) = C (t)+ I (t). Нормы амортизации физического и человеческого капитала совпадают, поэтому
Предполагается, что ресурсы полностью взаимозаменяемы, поэтому в стационарном состоянии их предельные производительности должны уравниваться. Из этого следует, что должно выполняться равенство:
Из последнего равенства следует, что
и производственная функция принимает вид:
где Модель (1) получила название «модель AK». Ее основное свойство – постоянная предельная производительность капитала в отличие от модели Солоу, в которой предполагается убывающая предельная производительность фактора. Все остальные предпосылки модели Солоу остаются в силе, и можно записать:
Учитывая, что Таким образом, темп роста капиталовооруженности постоянный и не зависит от k, т.е. капиталовооруженность всегда растет с постоянным темпом. Темпы роста выпуска и потребления на одного рабочего в любой момент времени также равны темпу роста капиталовооруженности:
т.е.
Раздел 5. Экономический рост, его моделирование, учет состояния экологии и социальной сферы в экономико-математических моделях Модели экономического роста широко представлены в экономических исследованиях. На основе этих моделей решаются разнообразные задачи анализа и прогнозирования развития национальных экономик. Современные модели экономического роста учитывают возможность инвестирования не только в физический капитал, но и в ряд других производственных ресурсов. Это связано с признанием того, что росту эффективности использования производственных ресурсов способствует большое число технологических, организационных и других факторов, совокупность которых охватывается понятием научно-технологического прогресса (НТП). Кроме того, в последние годы появляется все больше работ, в которых исследуется, как рост производства отражается на экологической ситуации, как экология влияет на возможность роста, как уровень экономического развития связан с различными показателями, характеризующими состояние социальной сферы. Однако не уделяется должного внимания взаимному влиянию экономики, экологии и социальной сферы несмотря на стремление многих стран мира к устойчивому развитию, под которым понимают развитие, удовлетворяющее потребности как настоящего, так и будущего поколений в экономических и экологических благах. Это означает рост валового внутреннего продукта (ВВП) при одновременном снижении антропогенной нагрузки на окружающую среду. Понятие устойчивого развития также включает в себя проблемы сокращения разрыва в уровнях экономического развития различных стран и благосостояния их населения, безопасности и т.д. Решение данных проблем требует использования методов экономико-математического моделирования экономического роста с учетом экологического и социального факторов. Экзогенный – внешний; эндогенный – внутренний.
|
||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 316; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.201.101 (0.006 с.) |

 ,
, ,
,  – технологический параметр,
– технологический параметр,  , H (t) – уровень человеческого капитала, которым обладает типичный представитель рабочей силы в момент времени t, L (t)=
, H (t) – уровень человеческого капитала, которым обладает типичный представитель рабочей силы в момент времени t, L (t)=  – численность населения, совпадающая с численностью рабочей силы, n
– численность населения, совпадающая с численностью рабочей силы, n  0.
0. I (t).
I (t). .
. .
. ,
, , (1)
, (1) – положительная константа.
– положительная константа. .
. , темп роста капиталовооруженности
, темп роста капиталовооруженности  можно найти из соотношения
можно найти из соотношения  .
.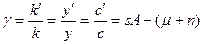 ,
, зависит от поведения параметров модели, например, более высокая норма накопления приведет к повышению долгосрочных темпов роста
зависит от поведения параметров модели, например, более высокая норма накопления приведет к повышению долгосрочных темпов роста  и темпа роста населения n также имеет постоянный эффект на темп роста
и темпа роста населения n также имеет постоянный эффект на темп роста 


