
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерий Коши существования предела функцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Предел суммы Предел суммы двух функций равен сумме пределов этих функций:
Предел произведения Предел произведения двух функций равен произведению пределов этих функций (при условии, что последние существуют):
Предел частного Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:
Определения предела функции по Коши и по Гейне. Их эквивалентность. Определение по Коши: f(x) сходится к числу А при хх0 если Е>0 >0: 0<|х-х0|< & хDf => |f(x)-А|<Е Теорема: Два определения эквивалентны: Д-во: Для эквивалентности определений достаточно доказать, что из сходимости по Коши следует сходимость по Гейне и из сходимости по Гейне следует сходимость по Коши. 1) (К)=>(Г) Е>0 >0: 0<|х-х0|< & хDf => |f(x)-А|<Е - определение Коши хNх0, хNх0, т.к. хNх0 => n0: n>n0 0<|xN-x0|<Е (Е=) => 0<|xN-x0|< => по определению Коши |f(xN)-А|<Е 2) (Г)=>(К) Воспользуемся законом логики: Если из отрицания B следует отрицание А, то из А следует В: Таким образом нам надо доказать что из отрицания (К) => отрицание (Г) Отрицание (К): Е>0: >0 x: 0<|x-x0|< => |f(x)-A|E Отрицание (Г): хNх0, хNх0: |f(xN)-A|E хNх0, хNх0 => n0: n>n0 0<|xN-x0|<Е (Е=) => по отрицанию определения Коши |f(xN)-А|Е Для ф-ции хf(х) определенной на интервале (а,+), определяется предел при хN следующим образом: limf(х) при хN = Limf(1/t) t+0 (если последний существует). Таким же образом определяются Lim f(х) при хN = Lim f(1/t) t0 и хN = lim f(1/t) t0 Критерий Коши существования предела функции Функции многих переменных Критерий Коши существования конечного предела. Для существования конечного предела "e>0$d>0"x¢,x¢¢ÎDÇ Доказательство проводится так же, как и для функции одного переменного. Необходимость. e>0,e/2®$ Достаточность. Пусть {xk} последовательность типа Гейне. Тогда {f(xk)} будет удовлетворять условию Коши для последовательностей, поэтому существует некоторый предел
Эта последовательность будет последовательностью типа Гейне и, как уже доказано, предел Предел сложной функции. Непрерывность сложной функции. Определение Функция Пусть функция у = φ (x) непрерывна в точке х 0, а функция f (y) непрерывна в точке у 0 = φ (x 0), тогда сложная функция f (φ(x)) непрерывна в точке х 0.
Указанное выше свойство можно сформулировать в виде правила замены переменной: пусть функция у = φ (x) непрерывна в точке х 0, а функция f (y) непрерывна в точке у 0 = φ(x 0), тогда
Определение монотонной функции. Теорема Вейерштрасса о существовании односторонних пределов у монотонной функции Монотонные функции Функция называется возрастающей на отрезке [ а, b ], принадлежащем области определения функции, если любому большему значению аргумента из этого отрезка соответствует большее значение функции x 2 > x 1→ f (x 2) > f (x 1) Функция называется убывающей на отрезке [ a, b ], если любому большему значению аргумента из этого интервала соответствуют меньшие значения функции x 2 > x 1→ f (x 2) < f (x 1) Функции, убывающие или возрастающие на некотором числовом промежутке, называются монотонными функциями. Участки возрастания функции на рисунке отмечены синим цветом (в чёрно белом варианте более толстым форматом).
Св-ва показательной функции Свойства: x,yÎR. 1) aX * aY = aX+Y xN®x, yN®y => aXn * aYn = aXn+Yn => Lim aXn * aYn = Lim aXn+Yn => Lim aXn * lim aYn = Lim aXn+Yn => aX * aY = aX+Y 2) aX / aY = aX-Y 3) (aX)Y=aX*Y xN®x, yK®y => (aXn)Yk = aXn*Yk => (n®¥) (aX)Yk=aX*Yk =>(k®¥) (aX)Y=aX*Y 4) x<y => aX<aY (a>1) - монотонность. x<x’ x,x’ÎR; xN®x x’N®x’ xN,x’NÎQ => xN<x’N => aXn < aX’n => (n®¥) aX£aX’- монотонна x-x`>q>0 => aX-X’ ³ aQ>1 => aX-X’¹1 => aX<aX’ - строго монотонна 5) при x n®0 aX ®1 Т.к. Lim a1/N=1 (n®¥), очевидно, что и Lim a-1/N=Lim1/a1/N=1 (n®¥). Поэтому "Е>0 $n0: "n>n0 1-E<a-1/N<a1/N<1+E, а>1. Если теперь |x|<1/n0, то a-1/N<aX<a1/N => 1-E<aX<1+E. => Lim aX=1 (при x®0) 6) aX - непрерывна Lim aX=1 (n®0) из (5) - это означает непрерывность aX в точке 0 => aX-aXo= aXo(aX-Xo - 1) при х®x0 x-x0 n®0 => aX-x0 n®1 => при х®x0 lim(aX - aXo)= Lim aXo*Lim(aX-Xo - 1) = x0 * 0 = 0 => aX - непрерывна 18.Последовательность (1+1/n)n и ее предел. xN= xN монотонно возрастает: докажем:
xN=(1+1/n)n=1+ n/1!*1/n + n*(n-1)/2!*1/n2 +... < 1 + 1/1! + 1/2!+...+1/n! = yN => yN<zN<3 Воспользуемся неравенством Бернулли (1+x)n³1+nx, x>-1) (доказывается по индукции): x=1/n => (1+1/n)n³1+n/n=2 Получили: 2 £ xN<3 => xN - ограничена, учитывая что xN - монотонно возрастает => xN - сходится и ее пределом является число е. Предел суммы Предел суммы двух функций равен сумме пределов этих функций:
Предел произведения Предел произведения двух функций равен произведению пределов этих функций (при условии, что последние существуют):
Предел частного Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:
Определения предела функции по Коши и по Гейне. Их эквивалентность. Определение по Коши: f(x) сходится к числу А при хх0 если Е>0 >0: 0<|х-х0|< & хDf => |f(x)-А|<Е Теорема: Два определения эквивалентны: Д-во: Для эквивалентности определений достаточно доказать, что из сходимости по Коши следует сходимость по Гейне и из сходимости по Гейне следует сходимость по Коши. 1) (К)=>(Г) Е>0 >0: 0<|х-х0|< & хDf => |f(x)-А|<Е - определение Коши хNх0, хNх0, т.к. хNх0 => n0: n>n0 0<|xN-x0|<Е (Е=) => 0<|xN-x0|< => по определению Коши |f(xN)-А|<Е 2) (Г)=>(К) Воспользуемся законом логики: Если из отрицания B следует отрицание А, то из А следует В: Таким образом нам надо доказать что из отрицания (К) => отрицание (Г) Отрицание (К): Е>0: >0 x: 0<|x-x0|< => |f(x)-A|E Отрицание (Г): хNх0, хNх0: |f(xN)-A|E хNх0, хNх0 => n0: n>n0 0<|xN-x0|<Е (Е=) => по отрицанию определения Коши |f(xN)-А|Е Для ф-ции хf(х) определенной на интервале (а,+), определяется предел при хN следующим образом: limf(х) при хN = Limf(1/t) t+0 (если последний существует). Таким же образом определяются Lim f(х) при хN = Lim f(1/t) t0 и хN = lim f(1/t) t0 Критерий Коши существования предела функции Функции многих переменных Критерий Коши существования конечного предела. Для существования конечного предела "e>0$d>0"x¢,x¢¢ÎDÇ Доказательство проводится так же, как и для функции одного переменного.
Необходимость. e>0,e/2®$ Достаточность. Пусть {xk} последовательность типа Гейне. Тогда {f(xk)} будет удовлетворять условию Коши для последовательностей, поэтому существует некоторый предел
Эта последовательность будет последовательностью типа Гейне и, как уже доказано, предел
|
|||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 456; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.213.201 (0.012 с.) |




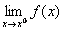 необходимо и достаточно, чтобы
необходимо и достаточно, чтобы :|f(x¢¢)-f(x¢)|<e.
:|f(x¢¢)-f(x¢)|<e.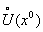 "xÎ
"xÎ  . Докажем, что для любой другой последовательности типа Гейне {yk} как в Гейне предел будет также равен B. Составим последовательность
. Докажем, что для любой другой последовательности типа Гейне {yk} как в Гейне предел будет также равен B. Составим последовательность
 должен существовать. Тогда все частичные пределы должны совпадать, в частности,
должен существовать. Тогда все частичные пределы должны совпадать, в частности,  =
=  .
. имеет предел
имеет предел  в точке
в точке  , предельной для области определения функции
, предельной для области определения функции  V(y 0), то значения функции f (y)
V(y 0), то значения функции f (y)  .
.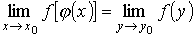
 х 1, x 2
х 1, x 2  ; yN=
; yN=  ; zN=yN +
; zN=yN + 




