
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Побудова «бажаної» лачх за номограмамиСодержание книги
Поиск на нашем сайте У цьому випадку для побудови «бажаної» ЛАЧХ використовуються чотири типи розімкненої астатичної ЛАЧХ (див. додаток В). Кожна типова ЛАЧХ повністю визначається чотирма параметрами: передаточним коефіцієнтом
Для усіх чотирьох типових ЛАЧХ складені номограми (приклади наведені в додатку В, рис. В.3), які за зазначеними вище параметрами дозволяють визначити основні динамічні характеристики замкнутої системи, що відповідає їм. Побудова «бажаної» ЛАЧХ за Санковским - Сигаловим Тут для синтезу можна використати дев'ять типів ЛАЧХ розімкненої системи, запропонованих авторами [17]. Форми типових асимптотичних ЛАЧХ і передаточні функції, що відповідають їм, наведені в додатку Г. Там же наводиться зв’язок частоти зрізу При виборі типу ЛАЧХ автори рекомендують дотримуватися таких міркувань: ü якщо сигнал завдання змінюється з великим прискоренням, а рівень перешкод малий, то вибираються ЛАЧХ типу 1 або 2; ü якщо сигнал завдання змінюється з невеликим прискоренням, а рівень перешкод великий, то вибираються ЛАЧХ типу 3, 4 або 5; ü якщо сигнал завдання змінюється з великим прискоренням і високий рівень перешкод, то вибираються ЛАЧХ типу 6 - 9. Для виконання синтезу системи за заданими показниками якості авторами запропоновано ряд емпіричних співвідношень, що зв’язують ці показники з параметрами ЛАЧХ.
Питання для самоконтролю і підготовки до тестового контролю 1. Форма і параметри яких характеристик прямо пов’язані з прямими показниками якості перехідних процесів? 2. Що ми передусім досягаємо введенням у прямий ланцюг системи управління корегуючих ланок? 3. У чому головна причина значного поширення методів синтезу на основі ЛАЧХ? 4. Що задають як вихідні дані для методів синтезу на основі ЛАЧХ? 5. Що таке «бажана» ЛАЧХ? 6. Що таке «незмінна» ЛАЧХ? 7. Як отримати ЛАЧХ коригуючої ланки, якщо відомі «бажана» і «незмінна» ЛАЧХ? 8. Для систем якого типу застосовується методи синтезу на основі ЛАЧХ? 9. На які ділянки умовно ділять «бажану» ЛАЧХ? 10. На які властивості системи переважно впливає характер поведінки «бажаної» ЛАЧХ в області низьких частот? 11. На які властивості системи переважно впливає характер поведінки «бажаної» ЛАЧХ в області середніх частот? 12. На які властивості системи переважно впливає характер поведінки «бажаної» ЛАЧХ в області високих частот? 13. Чим визначається нахил низькочастотної асимптоти «бажаної» ЛАЧХ? 14. Чим визначається ордината низькочастотної асимптоти «бажаної» ЛАЧХ на частоті 1 Гц? 15. Яка має бути ширина низькочастотної частини «бажаної» ЛАЧХ, щоб забезпечити якомога більшу смугу пропускання частот системою? 16. Яка частина ЛАЧХ системи найчастіше піддається корекції при синтезі? 17. З якою частиною ЛАЧХ системи пов’язано поняття «область значущих частот»? 18. Який нахил асимптоти «бажаної» ЛАЧХ найбільш характерний в області частоти зрізу? 19. Який нахил асимптоти «бажаної» ЛАЧХ треба мати в області високих частот? 20. Що необхідно додатково контролювати в області частоти зрізу при синтезі на основі ЛАЧХ? 21. Як отримують передаточну функцію коригуючої ланки при синтезі на основі ЛАЧХ? 22. Для чого використовують передаточну функцію коригуючої ланки при синтезі на основі ЛАЧХ? 23. Що є завершальним етапом синтезу на основі ЛАЧХ? 24. Який вид дійсної частотної характеристики береться як еталон при побудові «бажаної» ЛАЧХ методом Солодовникова? 25. Звідки отримують значення частоти зрізу при побудові «бажаної» ЛАЧХ методом Солодовникова? 26. Яку частоту: верхню або нижню обмежує максимально допустиме прискорення виконавчого органу при побудові «бажаної» ЛАЧХ методом Солодовникова? 27. Що використовується як еталон при побудові «бажаної» ЛАЧХ за номограмами? 28. Які додаткові вимоги враховують при виборі типової ЛАЧХ при побудові «бажаної» ЛАЧХ за методом Санковського-Сигалова? Лекція 20 9.4.2 Структурно-параметричний синтез ідеального регулятора (регулятор Ресвіка) Цей метод ще відомий як метод зворотного оператора. У найпростішому випадку, коли збурювальна дія на об’єкт відсутня (
Оскільки передаточна функція системи дорівнюватиме одиниці
те це означає, що сигнал завдання миттєво відтворюється вихідною величиною, тобто Якщо на об’єкт діє збурення
Таким чином, корисна складова
При точній еквівалентності об’єкта управління і його моделі Технічна реалізація безінерційного (ідеального) регулятора неможлива, проте така структура є ідеалом, до якого необхідно прагнути при синтезі високоякісних систем управління. Відповідно до ідеальної структури (рис. 9.17 б) можна сформулювати фундаментальний принцип структурно-параметричної оптимізації САУ із зворотним зв’язком: ідеальний регулятор повинен включати динамічну ланку з передаточною функцією, що дорівнює або є близькою зворотній передаточній функції об’єкта управління. На практиці часто доводиться розв’язувати задачу синтезу САУ інерційними об’єктами управління із запізнюванням, які можна описати такою узагальненою передаточною функцією
де Визначимо структуру і передаточну функцію ідеального регулятора для подібного роду об’єктів управління. Підставляючи значення передаточної функції
Проте тут є співмножник
Прирівнюючи праві частини виразів (9-47) і (9-48) та враховуючи в них значення передаточної функції
Розв’язуючи це рівняння стосовно
Цій передаточній функції відповідає структурна схема САУ (рис. 9.18), яка вже не містить упереджувача.
Це означає, що дія збурення Загальним недоліком даного підходу є необхідність знання точної математичної моделі об’єкта управління. Якщо модель відома неточно або параметри об’єкта змінюються в часі, ефект від використання регулятора Ресвіка істотно знижується. Якщо об’єкт управління апроксимувати моделлю першого порядку (аперіодичною ланкою), тоді, вважаючи запізнювання моделі об’єкта
За умови дії сигналів, що змінюються відносно повільно, можна прийняти
Можна помітити, що таку саму передаточну функцію має пропорційно-інтегральний регулятор (ПІ-регулятор) з параметрами настроювань Представивши об’єкт управління моделлю у вигляді ланки другого порядку і виконавши аналогічні перетворення, можна отримати передаточну функцію ідеального регулятора, яка вже відповідає ПІД-регулятору. На підставі отриманих співвідношень між параметрами об’єкта управління і регулятора можна сформулювати рекомендації щодо вибору типу регулятора і його параметрів настроювань: ü для об’єктів із запізнюванням, інерційна складова яких дійсно близька до ланки першого порядку (а не просто апроксимована такою ланкою!), доцільно застосовувати ПІ-регулятор; ü для об’єктів із запізнюванням, інерційна частина яких має порядок n ³ 2, найкращим регулятором є ПІД-регулятор. Узагальнення результатів експериментальних досліджень з визначення параметрів настроювань типових регуляторів для об’єктів із запізнюванням (при Таблиця 9.3 – Емпіричні формули для розрахунку настроювань типових регуляторів для об’єкта управління другого порядку із запізнюванням
Проведені дослідження дозволили також сформулювати такі загальні висновки щодо впливу параметрів настроювань на показники якості регулювання: · збільшення коефіцієнта k1 пропорційної частини регулятора призводить до збільшення перерегулювання · збільшення коефіцієнта k0 інтегральної частини регулятора призводить до зменшення часу перехідного процесу tр і збільшення перерегулювання · збільшення коефіцієнта k2 диференціальної частини регулятора призводить до зменшення часу tр перехідного процесу tр і збільшення перерегулювання
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 435; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.008 с.) |

 розімкненої системи (добротністю за швидкістю) і з’єднувальними частотами
розімкненої системи (добротністю за швидкістю) і з’єднувальними частотами (9-41)
(9-41) із передаточним коефіцієнтом
із передаточним коефіцієнтом 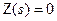 ), управління можна здійснювати за розімкненою схемою (рис. 9.16 а) при передаточній функції регулятора
), управління можна здійснювати за розімкненою схемою (рис. 9.16 а) при передаточній функції регулятора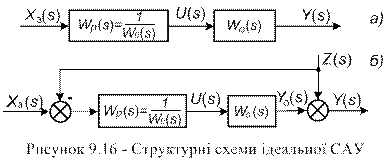
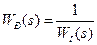 . (9-42)
. (9-42)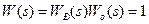 , (9-43)
, (9-43)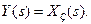 Такий перехідний процес і структуру, що реалізовує його, називають ідеальними.
Такий перехідний процес і структуру, що реалізовує його, називають ідеальними.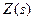 , яке можна виміряти, то теоретично можна синтезувати ідеальну розімкнену САУ (рис. 9.16 б) з повною компенсацією цього збурення, подавши його із зворотним знаком на вхід регулятора з передаточною функцією (9-42). Дійсно, у цьому випадку при
, яке можна виміряти, то теоретично можна синтезувати ідеальну розімкнену САУ (рис. 9.16 б) з повною компенсацією цього збурення, подавши його із зворотним знаком на вхід регулятора з передаточною функцією (9-42). Дійсно, у цьому випадку при 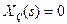 вихідна величина
вихідна величина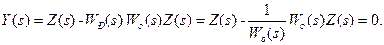 (9-44)
(9-44)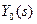 на виході об’єкта повністю урівноважуватиме (компенсуватиме) збурення
на виході об’єкта повністю урівноважуватиме (компенсуватиме) збурення 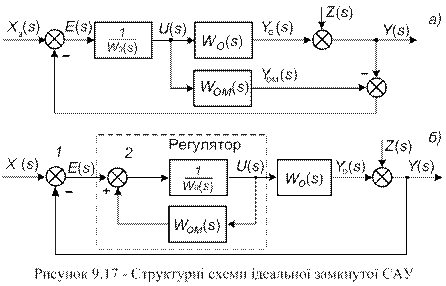
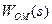 (рис. 9.17 а). Очевидно, що при
(рис. 9.17 а). Очевидно, що при 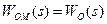 обчислюваний на виході моделі об’єкта сигнал
обчислюваний на виході моделі об’єкта сигнал 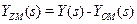 є опосередковано виміряним збуренням
є опосередковано виміряним збуренням 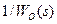 виявиться охопленим внутрішнім додатним зворотним зв’язком, а сигнал після суматора 1 відповідатиме сигналу помилки
виявиться охопленим внутрішнім додатним зворотним зв’язком, а сигнал після суматора 1 відповідатиме сигналу помилки 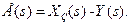 Це означає, що САУ стала замкнутою і працює за принципом від’ємного зворотного зв’язку з регулятором (див. рис. 9.17 б), що має передаточну функцію
Це означає, що САУ стала замкнутою і працює за принципом від’ємного зворотного зв’язку з регулятором (див. рис. 9.17 б), що має передаточну функцію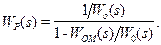 (9-45)
(9-45)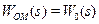 регулятор працюватиме як пропорційний (безінерційний) з коефіцієнтом посилення
регулятор працюватиме як пропорційний (безінерційний) з коефіцієнтом посилення 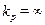 , що відповідає нульовим помилкам за каналами завдання і збурення.
, що відповідає нульовим помилкам за каналами завдання і збурення.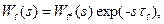 (9-46)
(9-46)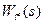 - дробово-раціональна функція, що характеризує інерційну частину об’єкта управління;
- дробово-раціональна функція, що характеризує інерційну частину об’єкта управління; 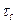 - чисте (транспортне) запізнювання об’єкта управління.
- чисте (транспортне) запізнювання об’єкта управління.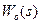 з виразу (9-46) у формулу (9-45), отримаємо передаточну функцію ідеального регулятора для інерційних об’єктів управління із запізнюванням:
з виразу (9-46) у формулу (9-45), отримаємо передаточну функцію ідеального регулятора для інерційних об’єктів управління із запізнюванням: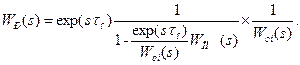 (9-47)
(9-47)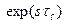 , який відповідає ідеальному упереджувачу (без мінуса), точна реалізація якого технічно неможлива. Для спрощення структури регулятора і полегшення його технічної реалізації робиться припущення, що для об’єктів управління з чистим запізнюванням
, який відповідає ідеальному упереджувачу (без мінуса), точна реалізація якого технічно неможлива. Для спрощення структури регулятора і полегшення його технічної реалізації робиться припущення, що для об’єктів управління з чистим запізнюванням 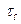 ідеальна САУ відтворює завдання не безінерційно, а із запізнюванням
ідеальна САУ відтворює завдання не безінерційно, а із запізнюванням 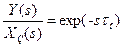 . З іншого боку, відповідно до правила (5-8) структурних перетворень для типової одноконтурної САУ (рис. 5.5) справедливо
. З іншого боку, відповідно до правила (5-8) структурних перетворень для типової одноконтурної САУ (рис. 5.5) справедливо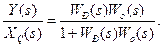 (9-48)
(9-48)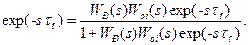 (9-49)
(9-49) , знаходимо передаточну функцію ідеального регулятора (регулятора Ресвіка):
, знаходимо передаточну функцію ідеального регулятора (регулятора Ресвіка):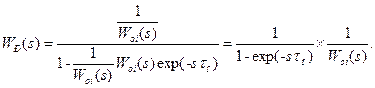 (9-50)
(9-50)
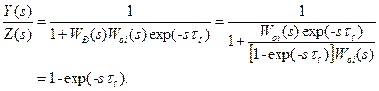 (9-51)
(9-51) , яким охоплюється ідеальний регулятор, іноді називають упереджувачем Сміта.
, яким охоплюється ідеальний регулятор, іноді називають упереджувачем Сміта. таким, що дорівнює чистому запізнюванню
таким, що дорівнює чистому запізнюванню  (9-52)
(9-52) , після чого, враховуючи цю рівність у виразі (9-52), отримаємо шукану передаточну функцію регулятора
, після чого, враховуючи цю рівність у виразі (9-52), отримаємо шукану передаточну функцію регулятора . (9-53)
. (9-53) і
і 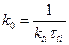 , вираженими через параметри об’єкта управління.
, вираженими через параметри об’єкта управління. ) для різних вимог до якості перехідних процесів дозволило отримати емпіричні формули, наведені в табл. 9.3.
) для різних вимог до якості перехідних процесів дозволило отримати емпіричні формули, наведені в табл. 9.3.




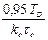

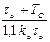






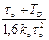



 і часу перехідного процесу tр та зменшення міри згасання
і часу перехідного процесу tр та зменшення міри згасання  ;
;


