
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розрахунок оптимальних налаштувань регулятора методом розширених частотних характеристик (щодо обмеження на міру загасання)Содержание книги
Поиск на нашем сайте
Метод розроблено професором Е. Г. Дудніковим (1956 р.). Ідея методу базується на зв'язку міри коливальності перехідного процесу із запасом стійкості при допущенні, що перехідний процес в основному визначається парою найближчих до уявної осі комплексно-зв'язаних коренів. Як типовий береться перехідний процес із мірою загасанняψ = 0,75 ÷ 0,9, і проводиться розрахунок настроювань регулятора, які забезпечують запас стійкості, що відповідає прийнятій мірі коливальності з використанням розширених частотних характеристик. Відомо, що чим далі корінь характеристичного рівняння системи віддалений від уявної осі (див. лекцію 12, п.7.2.2.2), тим менший вклад відповідної йому складової розв’язку диференціального рівняння в результуючий перехідний процес. Якщо знехтувати впливом усіх коренів характеристичного рівняння, окрім найближчих до уявної осі, то, по суті, система n -го порядку може бути представлена системою 2-го порядку (тобто коливальною ланкою). Позначимо найближчий до уявної осі корінь через
При m= 0маємо незгасаючий перехідний процес (межа стійкості), а при m=∞ - аперіодичний перехідний процес.
Ступінь загасання визначається (лекція 11, формула 7-11) як
де 2π m - логарифмічний декремент загасання коливань. У таблиці 9.1 наведені деякі значення ψ і значення m, що відповідають їм. Таблиця 9.1 - Відповідність між мірою коливальності m і мірою загасання ψ
Для забезпечення заданої міри коливальності m зад найближчий до уявної осі корінь повинен розміщуватися на прямій ОА, проведеній під кутом Рівняння прямої ОА на комплексній площині коренів(s=jω - рівняння уявної осі)
Уведемо поняття розширеної частотної характеристики. Відомо (див. лекцію 5), що звичайні частотні характеристики можуть бути отримані з передаточної функції формальною заміною Для експериментального отримання РЧХ необхідно створити періодичне вхідне збурення не з постійною, а із загасаючою амплітудою Приклади виразів для побудови РЧХ деяких елементарних ланок і типових регуляторів показані в додатку Б (таблиці Б.1 і Б.2). Звичайні частотні характеристики використовуються при дослідженні стійкості САУ за допомогою критеріїв Михайлова і Найквіста. Якщо ці критерії переформулювати для РЧХ, то з'являється можливість дослідження систем на задану міру коливальності перехідного процесу. Так, критерій Найквіста для РЧХ формулюється таким чином: якщо розімкнена система має міру коливальності не менше заданої ( За допомогою модифікованих критеріїв Найквіста або Михайлова для РЧХ можна побудувати лінії рівного загасання (ЛРЗ) системи, які є геометричним місцем точок у площині параметрів настроювань регулятора при заданому значенні показника коливальності mзад, серед яких і знаходяться оптимальні настроювання. Для отримання рівняння ЛРЗ необхідно записати умову знаходження системи на межі заданої міри коливальності. Ця умова для критерію Найквіста подається у вигляді умов виконання балансу амплітуд і фаз:
а для критерію Михайлова - у вигляді рівності нулю дійсної і уявної частин розширеної функції Михайлова (використовується рідше):
Підставляючи в (9-18) або (9-19) вирази для РЧХ об'єкта управління і регулятора і розв’язуючи зазначені системи рівнянь стосовно параметрів настроювань регулятора, можна отримати рівняння ЛРЗ в параметричному вигляді (залежно від частоти Розрахунок оптимальних настроювань регулятора, що забезпечують задану міру коливальності, виконується в два етапи: - - визначення з безлічі настроювань на ЛРЗ тих, які забезпечують необхідну якість регулювання, що оцінюється, наприклад, з умови мінімуму квадратичного інтегрального критерію (чи з інших міркувань). Для регуляторів з одним параметром настроювання (П- і І-регулятори) виконується тільки перший етап, оскільки для них ЛРЗ вироджується в точку. Для регуляторів з двома параметрами настроювання (параметри повинні бути незалежними!) після побудови ЛРЗ необхідно вибрати лише одну пару настроювань Для точного визначення оптимальних настроювань необхідно розрахувати інтегральний критерій для усіх пар значень
Питання для самоконтролю і підготовки до тестового контролю 1. Для яких видів об'єктів використовується формульний метод визначення настроювань регуляторів? 2. Метод Циглера-Ніколса є точним чи наближеним методом настроювання регуляторів? 3. Яке настроювання і до якого моменту змінюють у методі Циглера-Ніколса на першому етапі настроювань? 4. У чому суть другого етапу настроювання за методом Циглера-Ніколса? 5. Чому метод розрахунку настроювань регулятора за номограмами точніший за формульний? 6. У чому головна перевага експериментальних методів настроювання регуляторів? 7. На основі якого методу настроювань базується експериментальний метод незгасаючих коливань? 8. Чому застосування методу незгасаючих коливань на практиці обмежене? 9. Із чим пов'язаний показник ступеня загасання перехідного процесу: із запасом стійкості чи з розміщенням найближчого до уявної осі кореня? 10. Системою якого порядку приблизно замінюється система управління при використанні методу розширених частотних характеристик? 11. Чим визначається величина показника міри коливальності системи? 12. Як отримується розширена частотна характеристика з передаточної функції системи? 13. Який сигнал потрібно подати на вхід системи для отримання розширеної частотної характеристики експериментально? 14. Якщо розширена частотна характеристика розімкненої системи з мірою коливальності m не охоплює точку (-1, j0), то що це означає для замкнутої системи? 15. У яких координатах будується лінія рівного загасання при використанні методу розширених частотних характеристик? 16. Які умови використовуються для отримання рівняння лінії рівного загасання з критерію Найквіста при використанні методу розширених частотних характеристик? 17. Що виконується на першому етапі визначення настроювань регулятора за методом розширених частотних характеристик? 18. Що виконується на другому етапі визначення настроювань регулятора за методом розширених частотних характеристик? 19. У скільки етапів виконується розрахунок настроювань П-регулятора за методом розширених частотних характеристик? 20. Які дві умови задовольняють настроювання регулятора при використанні методу розширених частотних характеристик? 21. Які критерії стійкості використовуються при побудові лінії рівного загасання при використанні методу розширених частотних характеристик? Лекція 18 9.2.7 Метод визначення оптимальних настроювань регулятора за частотним показником коливальності (метод В. Я. Ротача) Ідея методу полягає у виборі таких настроювань регулятора, щоб у найбільшій мірі наблизити АЧХ реальної системи управління до АЧХ ідеальної системи, яка є ідеальним фільтром, що не пропускає збурювальні (високочастотні) впливи і пропускає управляючі (низькочастотні). Як критерій оцінки якості береться частотний показник коливальності, однозначно пов'язаний із запасом стійкості і мірою загасання перехідного процесу системи. Поняття частотного показника коливальності системи. Відомо (див. лекцію 15), що відповідно до критерію Найквіста динамічна система, стійка в розімкненому стані, стає нестійкою після замикання негативним зворотним зв'язком, якщо АФЧХ розімкненої системи Модуль АФЧХ замкнутої системи
Чисельник виразу (9-20) для деякої фіксованої частоти
Оскільки більшість промислових регуляторів використовують інтегральну складову від помилки неузгодження (І-складову), то при З наведених міркувань виходить, що величина резонансного піку модуля АЧХ замкнутої системи може бути зручною мірою запасу стійкості системи. Якщо знайти вираз для визначення геометричного місця точок, де
тобто є однаковий запас стійкості, то можна визначити обмеження, що накладаються на розташування АФЧХ розімкненої системи З рис. 9.11 а безпосередньо випливає
Після нескладних перетворень перепишемо вираз (9-23) у вигляді
У лекції 17 (п. 9.2.6) вже обговорювалося питання зв'язку міри загасання перехідного процесу, що визначається як величина відносного зменшення амплітуди за один період (див. 9-16), з показником коливальності m для систем другого порядку. Для такої ланки також існує однозначний зв'язок (без доведення) і між максимумом модуля частотної характеристики, віднесеним до її значення при нульовій частоті Таблиця 9.2 - Залежність між мірою загасання ψ і показником коливальності
Таким чином, показник коливальності системи Методика графоаналітичного методу визначення настроювань регулятора за показником коливальності. Вихідними даними для розрахунку є частотні характеристики об'єкта і необхідна (задана) міра загасання перехідного процесу ψ. Відповідно до прийнятого критерію розрахунок настроювань регулятора виконується в два етапи: 1. На першому етапі в просторі варійованих параметрів настроювань регулятора визначається межа області, в якій замкнута система управління матиме запас стійкості не нижче заданого показником коливальності 2. На другому етапі у знайденій області (чи на її межі) відшукується точка, що відповідає мінімуму помилки регулювання, тобто мінімуму відхилення частотних характеристик реальної системи від ідеальної. Ідеальною системою вважається така, яка має властивості ідеального фільтра, тобто в усьому діапазоні частот її АЧХ стосовно збурювальних дій дорівнює нулю ( Виконання першого етапу зручно робити графоаналітичним методом: будується АФЧХ розімкненої системи Порядок визначення граничного значення коефіцієнта
З урахуванням останньої обставини визначення граничного значення коефіцієнта передачі регулятора 1. Частотна передаточна функція регулятора записується у вигляді
2. З початку координат проводиться пряма ОЕ (рис. 9.13) під кутом, що визначається виразом (9-25). 3. Креслимо коло з центром на від'ємній дійсній півосі, яке торкалося б одночасно як АФЧХ 4. Відношення необхідного радіуса кола
Замість радіуса кола можна аналогічно використати координати його центра. 5. За наявності двох параметрів настроювань регулятора (наприклад,
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 600; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.101.250 (0.009 с.) |

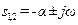 (рис. 9.8). Ступінь коливальності m - це тангенс кута γ між прямою ОА і уявною віссю (в п.7.2.2.2 лекції 12 ми користувалися для позначення кореневого показника коливальності величиною
(рис. 9.8). Ступінь коливальності m - це тангенс кута γ між прямою ОА і уявною віссю (в п.7.2.2.2 лекції 12 ми користувалися для позначення кореневого показника коливальності величиною 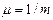 ):
):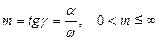 . (9-15)
. (9-15)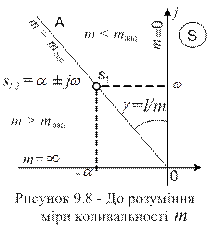 Для коливальної ланки 2 -го порядку між показником міри коливальності m і мірою згасання ψ (одна із прямих оцінок якості перехідного процесу, див. лекцію 11) існує однозначний зв'язок.
Для коливальної ланки 2 -го порядку між показником міри коливальності m і мірою згасання ψ (одна із прямих оцінок якості перехідного процесу, див. лекцію 11) існує однозначний зв'язок.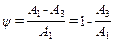 . Підставивши замість амплітуд їх значення для моментів часу
. Підставивши замість амплітуд їх значення для моментів часу 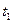 і
і 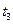 (див. рис. 9.9), а також з урахуванням (9-11) і очевидного співвідношення
(див. рис. 9.9), а також з урахуванням (9-11) і очевидного співвідношення 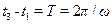 , отримаємо
, отримаємо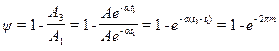 , (9-16)
, (9-16)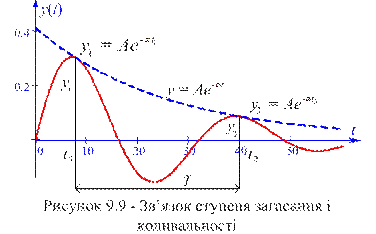
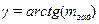 до уявної осі. Таким чином, пряма ОА може розглядатися як межа області заданої коливальності, а сама область буде розміщена ліворуч від прямої (рис. 9.8).
до уявної осі. Таким чином, пряма ОА може розглядатися як межа області заданої коливальності, а сама область буде розміщена ліворуч від прямої (рис. 9.8).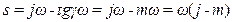 . (9-17)
. (9-17)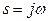 . У цьому випадку змінна
. У цьому випадку змінна 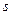 змінюється уздовж уявної осі. Розширеними частотними характеристиками називаються такі, в яких рух змінної
змінюється уздовж уявної осі. Розширеними частотними характеристиками називаються такі, в яких рух змінної 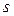 виконується уздовж межі заданої міри коливальності, тобто необхідно виконати заміну (9-17), а саме
виконується уздовж межі заданої міри коливальності, тобто необхідно виконати заміну (9-17), а саме 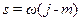 . Розширена частотна характеристика (РЧХ) позначається символом
. Розширена частотна характеристика (РЧХ) позначається символом 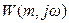 .
.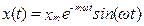 . Через складність постановки подібних експериментів в інженерній практиці РЧХ отримують аналітичним шляхом за передаточною функцією або методом перебудови звичайної АФЧХ.
. Через складність постановки подібних експериментів в інженерній практиці РЧХ отримують аналітичним шляхом за передаточною функцією або методом перебудови звичайної АФЧХ.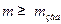 ), то міра коливальності замкнутої системи також буде не менше заданої, якщо розширена АФЧХ розімкненої системи при зміні частоти від 0 до ∞ не охопить точку з координатами [-1, j0]. Аналогічно модифікується і критерій Михайлова.
), то міра коливальності замкнутої системи також буде не менше заданої, якщо розширена АФЧХ розімкненої системи при зміні частоти від 0 до ∞ не охопить точку з координатами [-1, j0]. Аналогічно модифікується і критерій Михайлова.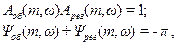 (9-18)
(9-18)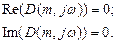 (9-19)
(9-19)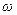 ), як це показано на рисунку 9.10.
), як це показано на рисунку 9.10.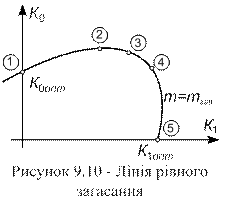 побудова в площині параметрів настроювань вибраного регулятора ЛРЗ, яка містить безліч настроювань, що забезпечують задану міру коливальності (чи заданий запас стійкості);
побудова в площині параметрів настроювань вибраного регулятора ЛРЗ, яка містить безліч настроювань, що забезпечують задану міру коливальності (чи заданий запас стійкості);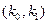 , яка відповідає мінімальному значенню інтегрального критерію. Досвід показує, що оптимальному значенню для ПІ-регулятора відповідає точка на ЛРЗ, що знаходиться дещо правіше за вершину (точка 3 на рисунку 9.10). Зміна настроювань у бік точки 2 посилює інтегральну складову, і в точці 1 регулятор працює як інтегральний. Аналогічно точці 5 відповідає оптимальне налаштування П-регулятора.
, яка відповідає мінімальному значенню інтегрального критерію. Досвід показує, що оптимальному значенню для ПІ-регулятора відповідає точка на ЛРЗ, що знаходиться дещо правіше за вершину (точка 3 на рисунку 9.10). Зміна настроювань у бік точки 2 посилює інтегральну складову, і в точці 1 регулятор працює як інтегральний. Аналогічно точці 5 відповідає оптимальне налаштування П-регулятора.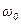 з виразу
з виразу 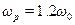 , чи за частотою
, чи за частотою 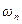 , що відповідає пропорційному закону регулювання за наближеною формулою
, що відповідає пропорційному закону регулювання за наближеною формулою 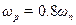 . Значення
. Значення 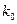 і
і 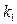 для знайденої частоти
для знайденої частоти 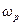 визначаються з параметричних рівнянь ЛРЗ.
визначаються з параметричних рівнянь ЛРЗ.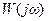 охоплює точку з координатами [-1;j0]. Чим далі від зазначеної «небезпечної» точки (управо, у бік початку координат) розміщується частотна характеристика, тим більший запас стійкості має система, а це безпосередньо пов'язано зі збільшенням міри загасання перехідних процесів і величиною (чи наявністю) резонансного піку модуля АФЧХ замкнутої системи (див. лекцію 12). Покажемо це.
охоплює точку з координатами [-1;j0]. Чим далі від зазначеної «небезпечної» точки (управо, у бік початку координат) розміщується частотна характеристика, тим більший запас стійкості має система, а це безпосередньо пов'язано зі збільшенням міри загасання перехідних процесів і величиною (чи наявністю) резонансного піку модуля АФЧХ замкнутої системи (див. лекцію 12). Покажемо це.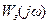 може бути виражений як
може бути виражений як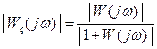 . (9-20)
. (9-20)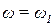 (рис. 9.11 а) дорівнює довжині вектора
(рис. 9.11 а) дорівнює довжині вектора 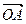 частотної характеристики
частотної характеристики 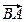 ,
,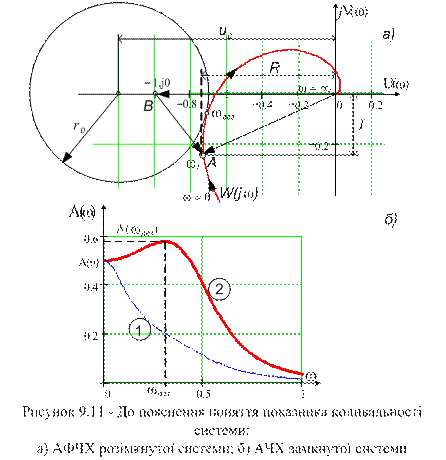
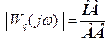 . (9-21)
. (9-21)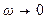 АФЧХ розімкненої системи йде у нескінченність, а відношення (9.21) - до одиниці. Хоча при зміні частоти від нуля до
АФЧХ розімкненої системи йде у нескінченність, а відношення (9.21) - до одиниці. Хоча при зміні частоти від нуля до 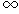 відношення (9-21) прямує до нуля, характер його зміни залежить від близькості АФЧХ від «небезпечної» точки [-1; j0]. Якщо АФЧХ розміщується досить далеко від цієї точки, то довжина відрізка АВ при русі уздовж кривої за стрілкою завжди більше довжини ОА, і тому відношення (9-21) із зростанням частоти зменшується монотонно. Це відповідає АЧХ, зображеній кривій 1 на рис. 9.11 б. Якщо ж АФЧХ наближається досить близько до «небезпечної» точки, то в певному діапазоні частот
відношення (9-21) прямує до нуля, характер його зміни залежить від близькості АФЧХ від «небезпечної» точки [-1; j0]. Якщо АФЧХ розміщується досить далеко від цієї точки, то довжина відрізка АВ при русі уздовж кривої за стрілкою завжди більше довжини ОА, і тому відношення (9-21) із зростанням частоти зменшується монотонно. Це відповідає АЧХ, зображеній кривій 1 на рис. 9.11 б. Якщо ж АФЧХ наближається досить близько до «небезпечної» точки, то в певному діапазоні частот 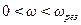 відношення (9-21) збільшуватиметься, що відповідає появі на АЧХ замкнутої системи резонансного піку на деякій частоті
відношення (9-21) збільшуватиметься, що відповідає появі на АЧХ замкнутої системи резонансного піку на деякій частоті 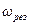 (крива 2 на рис. 9.11 б). Причому з побудови (рис. 9.11 а) видно, що величина піку збільшуватиметься у міру наближення
(крива 2 на рис. 9.11 б). Причому з побудови (рис. 9.11 а) видно, що величина піку збільшуватиметься у міру наближення 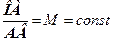 , (9-22)
, (9-22)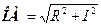 і
і 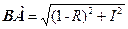 (теорема Піфагора). Тому, підставивши ці формули в (9-22) і піднісши до квадрату, отримаємо
(теорема Піфагора). Тому, підставивши ці формули в (9-22) і піднісши до квадрату, отримаємо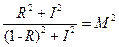 . (9-23)
. (9-23)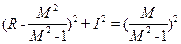 . (9-24)
. (9-24)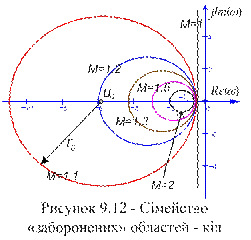 Отримане рівняння є рівнянням кола з радіусом
Отримане рівняння є рівнянням кола з радіусом 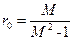 , центр якого лежить на від'ємній дійсній півосі на відстані
, центр якого лежить на від'ємній дійсній півосі на відстані 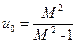 від початку координат. Таким чином, щоб резонансний пік модуля АЧХ замкнутої системи не перевищував деякої наперед заданої величини, що відповідає
від початку координат. Таким чином, щоб резонансний пік модуля АЧХ замкнутої системи не перевищував деякої наперед заданої величини, що відповідає 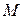 , необхідно, щоб АФЧХ розімкненої системи
, необхідно, щоб АФЧХ розімкненої системи 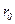 і
і 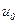 . Для різних значень
. Для різних значень 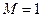 і в точку на осі при
і в точку на осі при 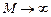 (див. рис. 9.12).
(див. рис. 9.12).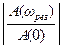 , і мірою загасання перехідного процесу ψ. Відношення
, і мірою загасання перехідного процесу ψ. Відношення 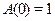 частотний показник коливальності повністю збігається з величиною
частотний показник коливальності повністю збігається з величиною 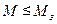 . При цьому вважається, що САУ має необхідний запас стійкості, якщо її показник коливальності знаходиться в діапазоні
. При цьому вважається, що САУ має необхідний запас стійкості, якщо її показник коливальності знаходиться в діапазоні 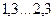 , що відповідає ступеню загасання ψ =0,95...0,75 (рекомендується брати М =1,6).
, що відповідає ступеню загасання ψ =0,95...0,75 (рекомендується брати М =1,6).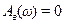 ), а по відношенню до сигналу управління - одиниці (
), а по відношенню до сигналу управління - одиниці (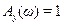 ). Оскільки в реальній системі виконання умови
). Оскільки в реальній системі виконання умови 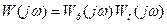 і знаходяться такі параметри настроювань регулятора, при яких ця характеристика торкатиметься кола для заданого значення
і знаходяться такі параметри настроювань регулятора, при яких ця характеристика торкатиметься кола для заданого значення 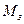 . При цьому варійованим параметром береться коефіцієнт передачі регулятора
. При цьому варійованим параметром береться коефіцієнт передачі регулятора 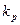 (у разі декількох параметрів настроювання процедура розрахунку залишається такою самою, проте змінюється обсяг обчислень через необхідність визначення найкращого значення
(у разі декількох параметрів настроювання процедура розрахунку залишається такою самою, проте змінюється обсяг обчислень через необхідність визначення найкращого значення 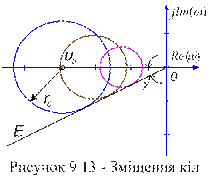
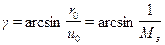 . (9-25)
. (9-25)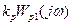 , де
, де 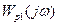 - частотна передаточна функція регулятора при значенні коефіцієнта передачі
- частотна передаточна функція регулятора при значенні коефіцієнта передачі 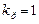 . За заданою передаточною функцією об'єкта управління
. За заданою передаточною функцією об'єкта управління 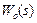 на комплексній площині будується АФЧХ розімкненої системи при одиничному коефіцієнті передачі регулятора і деяких фіксованих значеннях інших настроювань:
на комплексній площині будується АФЧХ розімкненої системи при одиничному коефіцієнті передачі регулятора і деяких фіксованих значеннях інших настроювань: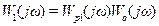 . (9-26)
. (9-26)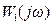 , так і прямої ОЕ.
, так і прямої ОЕ.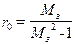 (див. 9-24) до отриманого значення радіуса
(див. 9-24) до отриманого значення радіуса 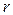 при побудові показує, у скільки разів необхідно змінити коефіцієнт передачі регулятора
при побудові показує, у скільки разів необхідно змінити коефіцієнт передачі регулятора 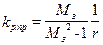 . (9-27)
. (9-27)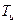 для ПІ-регулятора) визначення
для ПІ-регулятора) визначення 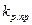 виконується для різних значень
виконується для різних значень 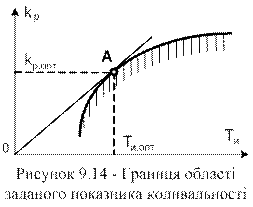 Другий етап. Доведено, що оптимальними по мінімуму середньоквадратичної помилки регулювання настроюваннями (при низькочастотних збуреннях) будуть такі настроювання, при яких система із заданим показником коливальності матиме найбільший коефіцієнт при інтегральній складовій, чому відповідає виконання умови
Другий етап. Доведено, що оптимальними по мінімуму середньоквадратичної помилки регулювання настроюваннями (при низькочастотних збуреннях) будуть такі настроювання, при яких система із заданим показником коливальності матиме найбільший коефіцієнт при інтегральній складовій, чому відповідає виконання умови 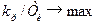 . Ця умова виконується в точці А, в якій пряма з кутовим коефіцієнтом
. Ця умова виконується в точці А, в якій пряма з кутовим коефіцієнтом 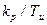 , що виходить з початку координат, торкається до границі області з необхідним запасом стійкості.
, що виходить з початку координат, торкається до границі області з необхідним запасом стійкості.


