
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорія автоматичного управлінняСодержание книги
Поиск на нашем сайте
Г. М. ХУДОЛЕЙ
ТЕОРІЯ АВТОМАТИЧНОГО УПРАВЛІННЯ
КОНСПЕКТ ЛЕКЦІЙ
У двох частинах Частина 2 Синтез лінійних систем автоматичного управління
Суми Сумський державний університет
Міністерство освіти і науки, молоді та спорту України Сумський державний університет Шосткинський інститут
ТЕОРІЯ АВТОМАТИЧНОГО УПРАВЛІННЯ
КОНСПЕКТ ЛЕКЦІЙ
для студентів спеціальності 6.050201 «Комп’ютеризовані системи управління та автоматика» усіх форм навчання
У двох частинах Частина 2 Синтез лінійних систем автоматичного управління
Затверджено на засіданні кафедри системотехніки та інформаційних технологій як конспект лекцій з дисципліни «Теорія автоматичного управління» Протокол № 01 від 31 серпня 2012 р.
Суми Сумський державний університет
Теорія автоматичного управління:конспект лекцій: у 2 частинах. Ч. 2 «Синтез лінійних систем автоматичного управління» / укладач Г. М. Худолей. – Суми: Сумський державний університет, 2012. - 87с.
Кафедра системотехніки та інформаційних технологій
ЗМІСТ С.
ВСТУП.. 6 Лекція 16. 7 9 Синтез лінійних безперервних систем автоматичного управління (САУ) 7 9.1 Постановка задачі синтезу САУ.. 7 9.1.1 Визначення поняття синтезу САУ.. 7 9.1.2 Вимоги до промислових систем управління (критеріальна стратегія синтезу) 8 9.1.3 Методологічні основи синтезу. 9 9.1.4 Основні етапи створення САУ.. 10 9.1.5 Класифікація методів розв’язання задач синтезу. 11 9.1.6 Коригуючі пристрої і способи їх включення в САУ.. 12 9.2 Наближені методи параметричного синтезу. 16 9.2.1 Типові закони управління, регулятори і особливості їх застосування 16 Лекція 17. 26 9.2.2 Формульний метод визначення настроювань регуля - тора. 26 9.2.3 Метод незгасаючих коливань (метод Циглера-Ніколса) 26 9.2.4 Метод налаштування регуляторів за номограмами. 28 9.2.5 Експериментальні методи настроювання регулятора. 29 9.2.6 Розрахунок оптимальних налаштувань регулятора методом розширених частотних характеристик (щодо обмеження на міру загасання) 31 Лекція 18. 38 9.2.7 Метод визначення оптимальних настроювань регулятора за частотним показником коливальності (метод В. Я. Ротача) 38
9.3 Точні методи параметричного синтезу. 45 9.3.1 Синтез системи управління за мінімумом інтегральної оцінки якості 45 Лекція 19. 51 9.4 Методи структурно-параметричного синтезу. 51 9.4.1 Синтез системи управління методом ЛАЧХ.. 51 Лекція 20. 63 9.4.2 Структурно-параметричний синтез ідеального регулятора (регулятор Ресвіка) 63 9.4.3 Метод стандартних перехідних функцій. 70 9.5 Реалізація коригуючих пристроїв (регуляторів) 72 9.5.1 Пасивні чотириполюсники постійного струму. 73 9.5.2 Активні чотириполюсники постійного струму. 74 Додаток А.. 78 Додаток Б.. 80 Додаток В.. 81 Додаток Г.. 83 Список рекомендованої літератури. 84
ВСТУП Однією з найважливіших складових автоматизації технологічних процесів є автоматичне управління, яке має на меті підтримку (стабілізацію) заданого значення регульованих змінних або їх зміну за заданим у часі законом (програмне регулювання) з необхідною точністю, що дозволяє забезпечити одержання продукції потрібної якості, а також безпечну й економічну роботу технологічного устаткування. Досягнення зазначеної мети можливе лише завдяки побудові або синтезу ефективних систем автоматичного управління. Цей конспект лекцій являє собою виклад другої, заключної, частини курсу лекцій «Теорія автоматичного управління», присвяченого центральній проблемі лінійної теорії автоматичного управління – задачі синтезу лінійних систем автоматичного управління, яка, у широкому сенсі, полягає у визначенні складу, структури (конфігурації) системи автоматичного управління, параметрів усіх її пристроїв і технічних засобів реалізації за умови задоволення заданого комплексу технічних вимог. Це завдання є досить складним, неоднозначним, та таким, що вимагає глибоких знань і творчого підходу при його розв'язанні. Якщо багато інших важливих задач теорії управління (як, наприклад, стійкість) вивчаються й іншими науками, то задача синтезу систем автоматичного управління – це задача безпосередньо самої теорії управління. Лекція 16 9 Синтез лінійних безперервних систем автоматичного управління (САУ) Постановка задачі синтезу САУ Основні етапи створення САУ Етапи створення САУ можна подати у такому порядку: Етап 1. Формулювання мети управління, вибір змінних, якими необхідно керувати, та каналів управління, формулювання вимог до них.
Етап 2. Вибір функціональної структури (конфігурації системи), місця включення коригуючих пристроїв. Етап 3. Побудова математичної моделі функціонально необхідних елементів (у тому числі, можливо, об'єкта управління), вибір виду задачі ідентифікації (параметрична або непараметрична). Етап 4. Вибір еталонної передаточної функції, перехідної або частотної характеристики, що задовольняють вимоги якості управління. Етап 5. Вибір та обґрунтування структури коригуючих пристроїв, розрахунок їх числових параметрів пристроїв. Етап 6. Моделювання та дослідження САУ, що синтезується, з точки зору досягнення мети управління. Якщо якість САУ не задовольняє вимоги, необхідно змінити структуру системи, більш конструктивно вибрати функціонально необхідні елементи з урахуванням умов роботи або змінити структуру регулятора. Етап 7. Формування технічного завдання, попереднє ескізне проектування, випробування дослідних зразків, впровадження у виробництво. Названі етапи створення САУ і їх порядок не є догмою – залежно від вибраного методу синтезу деякі етапи можуть бути пропущені або багаторазово повторені. Питання для самоконтролю і підготовки до тестового контролю 1. На які два великі класи поділяють усі математичні задачі ТАУ? 2. Яка із задач: аналізу або синтезу є зворотною задачею? 3. Які підзадачі розв’язуються в процесі розв’язання задачі синтезу САУ? 4. Які вихідні дані потрібні для синтезу САУ? 5. Відомо, що для синтезу САУ потрібні такі дані: математична модель ОУ і показники якості. Що із зазначеного є невід'ємною властивістю об'єкта? 6. Які основні вимоги висуваються до промислових систем управління? 7. Що належить до незмінної частини функціональної структури САУ? 8. Що належить до змінюваної частини функціональної структури САУ? 9. Що на практиці визначають в першу чергу при проектуванні: алгоритмічну чи функціональну структуру САУ? 10. Які дії необхідно зробити, якщо спроектована САУ не задовольняє вимоги? 11. Які способи включення коригуючи пристроїв вам відомі? 12. До якого способу включення коригуючого пристрою належить гнучкий зворотний зв'язок? 13. Для яких цілей в САУ застосовується регулятор? 14. Що технічно може включатися до складу регулятора? 15. Які два види регуляторів, що розрізняються за видами споживання енергії, ви знаєте? 16. У чому головна перевага регуляторів прямої дії? 17. Назвіть види регуляторів непрямої дії залежно від конкретного виду зовнішнього джерела енергії? 18. У чому переваги і недоліки електричних регуляторів непрямої дії? 19. Запишіть рівняння, що описує закон роботи П-регулятора. 20. Який головний недолік систем із П-регулятором? 21. Який із регуляторів П чи І забезпечує кращі динамічні характеристики системи? 22. Як можна поліпшити статичну точність систем із регулятором, у складі якого є пропорційна складова? 23. Яка головна перевага систем з І-регулятором? 24. Чи можна використати І-регулятор для управління об'єктами без самовирівнювання? 25. Які два параметри настроювань має ПІ-регулятор? 26. Як поводиться ПІ-регулятор в області низьких частот, а як - в області високих? 27. Що загального між І- і ПІ-регуляторами? 28. Від чого залежить сигнал управління, що виробляється ПД-регулятором?
29. Яка особливість ФЧХ сприяє поліпшенню стійкості систем з ПД-регулятором? 30. Через що ПД-регулятори не використовуються на практиці? 31. Які закони управління реалізовані в ПІД-регуляторі? 32. Які дві головні переваги властиві системам з ПІД-регулятором? 33. Чим реальні промислові регулятори відрізняються від ідеальних? Лекція 17 Питання для самоконтролю і підготовки до тестового контролю 1. Для яких видів об'єктів використовується формульний метод визначення настроювань регуляторів? 2. Метод Циглера-Ніколса є точним чи наближеним методом настроювання регуляторів? 3. Яке настроювання і до якого моменту змінюють у методі Циглера-Ніколса на першому етапі настроювань? 4. У чому суть другого етапу настроювання за методом Циглера-Ніколса? 5. Чому метод розрахунку настроювань регулятора за номограмами точніший за формульний? 6. У чому головна перевага експериментальних методів настроювання регуляторів? 7. На основі якого методу настроювань базується експериментальний метод незгасаючих коливань? 8. Чому застосування методу незгасаючих коливань на практиці обмежене? 9. Із чим пов'язаний показник ступеня загасання перехідного процесу: із запасом стійкості чи з розміщенням найближчого до уявної осі кореня? 10. Системою якого порядку приблизно замінюється система управління при використанні методу розширених частотних характеристик? 11. Чим визначається величина показника міри коливальності системи? 12. Як отримується розширена частотна характеристика з передаточної функції системи? 13. Який сигнал потрібно подати на вхід системи для отримання розширеної частотної характеристики експериментально? 14. Якщо розширена частотна характеристика розімкненої системи з мірою коливальності m не охоплює точку (-1, j0), то що це означає для замкнутої системи? 15. У яких координатах будується лінія рівного загасання при використанні методу розширених частотних характеристик? 16. Які умови використовуються для отримання рівняння лінії рівного загасання з критерію Найквіста при використанні методу розширених частотних характеристик? 17. Що виконується на першому етапі визначення настроювань регулятора за методом розширених частотних характеристик? 18. Що виконується на другому етапі визначення настроювань регулятора за методом розширених частотних характеристик? 19. У скільки етапів виконується розрахунок настроювань П-регулятора за методом розширених частотних характеристик? 20. Які дві умови задовольняють настроювання регулятора при використанні методу розширених частотних характеристик?
21. Які критерії стійкості використовуються при побудові лінії рівного загасання при використанні методу розширених частотних характеристик? Лекція 18 9.2.7 Метод визначення оптимальних настроювань регулятора за частотним показником коливальності (метод В. Я. Ротача) Ідея методу полягає у виборі таких настроювань регулятора, щоб у найбільшій мірі наблизити АЧХ реальної системи управління до АЧХ ідеальної системи, яка є ідеальним фільтром, що не пропускає збурювальні (високочастотні) впливи і пропускає управляючі (низькочастотні). Як критерій оцінки якості береться частотний показник коливальності, однозначно пов'язаний із запасом стійкості і мірою загасання перехідного процесу системи. Поняття частотного показника коливальності системи. Відомо (див. лекцію 15), що відповідно до критерію Найквіста динамічна система, стійка в розімкненому стані, стає нестійкою після замикання негативним зворотним зв'язком, якщо АФЧХ розімкненої системи Модуль АФЧХ замкнутої системи
Чисельник виразу (9-20) для деякої фіксованої частоти
Оскільки більшість промислових регуляторів використовують інтегральну складову від помилки неузгодження (І-складову), то при З наведених міркувань виходить, що величина резонансного піку модуля АЧХ замкнутої системи може бути зручною мірою запасу стійкості системи.
Якщо знайти вираз для визначення геометричного місця точок, де
тобто є однаковий запас стійкості, то можна визначити обмеження, що накладаються на розташування АФЧХ розімкненої системи З рис. 9.11 а безпосередньо випливає
Після нескладних перетворень перепишемо вираз (9-23) у вигляді
У лекції 17 (п. 9.2.6) вже обговорювалося питання зв'язку міри загасання перехідного процесу, що визначається як величина відносного зменшення амплітуди за один період (див. 9-16), з показником коливальності m для систем другого порядку. Для такої ланки також існує однозначний зв'язок (без доведення) і між максимумом модуля частотної характеристики, віднесеним до її значення при нульовій частоті Таблиця 9.2 - Залежність між мірою загасання ψ і показником коливальності
Таким чином, показник коливальності системи Методика графоаналітичного методу визначення настроювань регулятора за показником коливальності. Вихідними даними для розрахунку є частотні характеристики об'єкта і необхідна (задана) міра загасання перехідного процесу ψ. Відповідно до прийнятого критерію розрахунок настроювань регулятора виконується в два етапи: 1. На першому етапі в просторі варійованих параметрів настроювань регулятора визначається межа області, в якій замкнута система управління матиме запас стійкості не нижче заданого показником коливальності 2. На другому етапі у знайденій області (чи на її межі) відшукується точка, що відповідає мінімуму помилки регулювання, тобто мінімуму відхилення частотних характеристик реальної системи від ідеальної. Ідеальною системою вважається така, яка має властивості ідеального фільтра, тобто в усьому діапазоні частот її АЧХ стосовно збурювальних дій дорівнює нулю ( Виконання першого етапу зручно робити графоаналітичним методом: будується АФЧХ розімкненої системи Порядок визначення граничного значення коефіцієнта
З урахуванням останньої обставини визначення граничного значення коефіцієнта передачі регулятора 1. Частотна передаточна функція регулятора записується у вигляді
2. З початку координат проводиться пряма ОЕ (рис. 9.13) під кутом, що визначається виразом (9-25). 3. Креслимо коло з центром на від'ємній дійсній півосі, яке торкалося б одночасно як АФЧХ 4. Відношення необхідного радіуса кола
Замість радіуса кола можна аналогічно використати координати його центра. 5. За наявності двох параметрів настроювань регулятора (наприклад,
Питання для самоконтролю і підготовки до тестового контролю 1. Наближення якої характеристики до ідеальної або еталонної лежить в основі методу Ротача? 2. Як поводиться ідеальна АЧХ стосовно збурювальних і управляючих сигналів? 3. Що береться як критерій настроювання в методі Ротача? 4. Як веде себе показник ступеня згасання перехідного процесу, якщо запас стійкості системи збільшується? 5. Що можна сказати про показник ступеня згасання перехідного процесу, якщо величина резонансного піка модуля АФЧХ збільшується? 6. Мірою чого може бути величина резонансного піку модуля АФЧХ? 7. Показник коливальності М є геометричним місцем з однаковим …? Чим? 8. Чим визначається «заборонена» область на площині АФЧХ, що обмежує величину резонансного піка модуля АФЧХ замкнутої системи? 9. Запишіть вираз для визначення показника коливальності М через амплітуди частотної характеристики. 10. Чому ми можемо використати показник коливальності М як критерій при виборі налаштувань регулятора? 11. У якому діапазоні (приблизно) повинне знаходитися значення показника коливальності М для прийнятного запасу стійкості? 12. Що визначається на першому етапі синтезу системи за методом Ротача? 13. У чому полягає другий етап синтезу системи за методом Ротача? 14. Який параметр настроювань регулятора варіюється на першому етапі синтезу системи управління за методом Ротача? 15. Метод синтезу САУ за мінімумом інтегральної оцінки є точним, наближеним чи графоаналітичним? 16. З яких міркувань робиться вибір оптимальних настроювань регулятора при використанні інтегральних критеріїв якості? 17. Яку інтегральну оцінку якості найчастіше використовують при синтезі САУ? 18. Який можливий недолік використання квадратичного інтегрального критерію при синтезі САУ? 19. Використання покращаної квадратичної інтегральної оцінки наближає перехідну характеристику до …? До чого? 20. У чому основна технічна трудність використання квадратичного інтегрального критерію при синтезі САУ? 21. Якщо вже отримано вираз для інтегрального критерію як функція невідомих параметрів, що необхідно зробити далі? 22. Що потрібно зробити, якщо в результаті синтезу за мінімумом інтегрального критерію отримані незадовільні результати? Лекція 19 Питання для самоконтролю і підготовки до тестового контролю 1. Форма і параметри яких характеристик прямо пов’язані з прямими показниками якості перехідних процесів? 2. Що ми передусім досягаємо введенням у прямий ланцюг системи управління корегуючих ланок? 3. У чому головна причина значного поширення методів синтезу на основі ЛАЧХ? 4. Що задають як вихідні дані для методів синтезу на основі ЛАЧХ? 5. Що таке «бажана» ЛАЧХ? 6. Що таке «незмінна» ЛАЧХ? 7. Як отримати ЛАЧХ коригуючої ланки, якщо відомі «бажана» і «незмінна» ЛАЧХ? 8. Для систем якого типу застосовується методи синтезу на основі ЛАЧХ? 9. На які ділянки умовно ділять «бажану» ЛАЧХ? 10. На які властивості системи переважно впливає характер поведінки «бажаної» ЛАЧХ в області низьких частот? 11. На які властивості системи переважно впливає характер поведінки «бажаної» ЛАЧХ в області середніх частот? 12. На які властивості системи переважно впливає характер поведінки «бажаної» ЛАЧХ в області високих частот? 13. Чим визначається нахил низькочастотної асимптоти «бажаної» ЛАЧХ? 14. Чим визначається ордината низькочастотної асимптоти «бажаної» ЛАЧХ на частоті 1 Гц? 15. Яка має бути ширина низькочастотної частини «бажаної» ЛАЧХ, щоб забезпечити якомога більшу смугу пропускання частот системою? 16. Яка частина ЛАЧХ системи найчастіше піддається корекції при синтезі? 17. З якою частиною ЛАЧХ системи пов’язано поняття «область значущих частот»? 18. Який нахил асимптоти «бажаної» ЛАЧХ найбільш характерний в області частоти зрізу? 19. Який нахил асимптоти «бажаної» ЛАЧХ треба мати в області високих частот? 20. Що необхідно додатково контролювати в області частоти зрізу при синтезі на основі ЛАЧХ? 21. Як отримують передаточну функцію коригуючої ланки при синтезі на основі ЛАЧХ? 22. Для чого використовують передаточну функцію коригуючої ланки при синтезі на основі ЛАЧХ? 23. Що є завершальним етапом синтезу на основі ЛАЧХ? 24. Який вид дійсної частотної характеристики береться як еталон при побудові «бажаної» ЛАЧХ методом Солодовникова? 25. Звідки отримують значення частоти зрізу при побудові «бажаної» ЛАЧХ методом Солодовникова? 26. Яку частоту: верхню або нижню обмежує максимально допустиме прискорення виконавчого органу при побудові «бажаної» ЛАЧХ методом Солодовникова? 27. Що використовується як еталон при побудові «бажаної» ЛАЧХ за номограмами? 28. Які додаткові вимоги враховують при виборі типової ЛАЧХ при побудові «бажаної» ЛАЧХ за методом Санковського-Сигалова? Лекція 20 9.4.2 Структурно-параметричний синтез ідеального регулятора (регулятор Ресвіка) Цей метод ще відомий як метод зворотного оператора. У найпростішому випадку, коли збурювальна дія на об’єкт відсутня (
Оскільки передаточна функція системи дорівнюватиме одиниці
те це означає, що сигнал завдання миттєво відтворюється вихідною величиною, тобто Якщо на об’єкт діє збурення
Таким чином, корисна складова
При точній еквівалентності об’єкта управління і його моделі Технічна реалізація безінерційного (ідеального) регулятора неможлива, проте така структура є ідеалом, до якого необхідно прагнути при синтезі високоякісних систем управління. Відповідно до ідеальної структури (рис. 9.17 б) можна сформулювати фундаментальний принцип структурно-параметричної оптимізації САУ із зворотним зв’язком: ідеальний регулятор повинен включати динамічну ланку з передаточною функцією, що дорівнює або є близькою зворотній передаточній функції об’єкта управління. На практиці часто доводиться розв’язувати задачу синтезу САУ інерційними об’єктами управління із запізнюванням, які можна описати такою узагальненою передаточною функцією
де Визначимо структуру і передаточну функцію ідеального регулятора для подібного роду об’єктів управління. Підставляючи значення передаточної функції
Проте тут є співмножник
Прирівнюючи праві частини виразів (9-47) і (9-48) та враховуючи в них значення передаточної функції
Розв’язуючи це рівняння стосовно
Цій передаточній функції відповідає структурна схема САУ (рис. 9.18), яка вже не містить упереджувача.
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 447; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.140.99 (0.012 с.) |



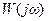 охоплює точку з координатами [-1;j0]. Чим далі від зазначеної «небезпечної» точки (управо, у бік початку координат) розміщується частотна характеристика, тим більший запас стійкості має система, а це безпосередньо пов'язано зі збільшенням міри загасання перехідних процесів і величиною (чи наявністю) резонансного піку модуля АФЧХ замкнутої системи (див. лекцію 12). Покажемо це.
охоплює точку з координатами [-1;j0]. Чим далі від зазначеної «небезпечної» точки (управо, у бік початку координат) розміщується частотна характеристика, тим більший запас стійкості має система, а це безпосередньо пов'язано зі збільшенням міри загасання перехідних процесів і величиною (чи наявністю) резонансного піку модуля АФЧХ замкнутої системи (див. лекцію 12). Покажемо це.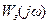 може бути виражений як
може бути виражений як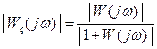 . (9-20)
. (9-20)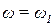 (рис. 9.11 а) дорівнює довжині вектора
(рис. 9.11 а) дорівнює довжині вектора 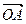 частотної характеристики
частотної характеристики 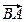 ,
,
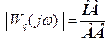 . (9-21)
. (9-21)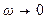 АФЧХ розімкненої системи йде у нескінченність, а відношення (9.21) - до одиниці. Хоча при зміні частоти від нуля до
АФЧХ розімкненої системи йде у нескінченність, а відношення (9.21) - до одиниці. Хоча при зміні частоти від нуля до 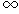 відношення (9-21) прямує до нуля, характер його зміни залежить від близькості АФЧХ від «небезпечної» точки [-1; j0]. Якщо АФЧХ розміщується досить далеко від цієї точки, то довжина відрізка АВ при русі уздовж кривої за стрілкою завжди більше довжини ОА, і тому відношення (9-21) із зростанням частоти зменшується монотонно. Це відповідає АЧХ, зображеній кривій 1 на рис. 9.11 б. Якщо ж АФЧХ наближається досить близько до «небезпечної» точки, то в певному діапазоні частот
відношення (9-21) прямує до нуля, характер його зміни залежить від близькості АФЧХ від «небезпечної» точки [-1; j0]. Якщо АФЧХ розміщується досить далеко від цієї точки, то довжина відрізка АВ при русі уздовж кривої за стрілкою завжди більше довжини ОА, і тому відношення (9-21) із зростанням частоти зменшується монотонно. Це відповідає АЧХ, зображеній кривій 1 на рис. 9.11 б. Якщо ж АФЧХ наближається досить близько до «небезпечної» точки, то в певному діапазоні частот 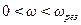 відношення (9-21) збільшуватиметься, що відповідає появі на АЧХ замкнутої системи резонансного піку на деякій частоті
відношення (9-21) збільшуватиметься, що відповідає появі на АЧХ замкнутої системи резонансного піку на деякій частоті 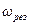 (крива 2 на рис. 9.11 б). Причому з побудови (рис. 9.11 а) видно, що величина піку збільшуватиметься у міру наближення
(крива 2 на рис. 9.11 б). Причому з побудови (рис. 9.11 а) видно, що величина піку збільшуватиметься у міру наближення 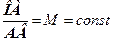 , (9-22)
, (9-22)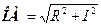 і
і 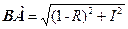 (теорема Піфагора). Тому, підставивши ці формули в (9-22) і піднісши до квадрату, отримаємо
(теорема Піфагора). Тому, підставивши ці формули в (9-22) і піднісши до квадрату, отримаємо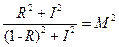 . (9-23)
. (9-23)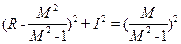 . (9-24)
. (9-24)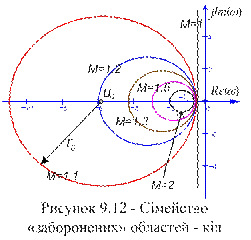 Отримане рівняння є рівнянням кола з радіусом
Отримане рівняння є рівнянням кола з радіусом 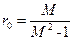 , центр якого лежить на від'ємній дійсній півосі на відстані
, центр якого лежить на від'ємній дійсній півосі на відстані 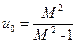 від початку координат. Таким чином, щоб резонансний пік модуля АЧХ замкнутої системи не перевищував деякої наперед заданої величини, що відповідає
від початку координат. Таким чином, щоб резонансний пік модуля АЧХ замкнутої системи не перевищував деякої наперед заданої величини, що відповідає 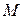 , необхідно, щоб АФЧХ розімкненої системи
, необхідно, щоб АФЧХ розімкненої системи 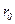 і
і 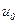 . Для різних значень
. Для різних значень 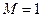 і в точку на осі при
і в точку на осі при 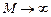 (див. рис. 9.12).
(див. рис. 9.12).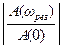 , і мірою загасання перехідного процесу ψ. Відношення
, і мірою загасання перехідного процесу ψ. Відношення 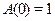 частотний показник коливальності повністю збігається з величиною
частотний показник коливальності повністю збігається з величиною 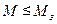 . При цьому вважається, що САУ має необхідний запас стійкості, якщо її показник коливальності знаходиться в діапазоні
. При цьому вважається, що САУ має необхідний запас стійкості, якщо її показник коливальності знаходиться в діапазоні 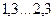 , що відповідає ступеню загасання ψ =0,95...0,75 (рекомендується брати М =1,6).
, що відповідає ступеню загасання ψ =0,95...0,75 (рекомендується брати М =1,6).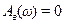 ), а по відношенню до сигналу управління - одиниці (
), а по відношенню до сигналу управління - одиниці (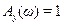 ). Оскільки в реальній системі виконання умови
). Оскільки в реальній системі виконання умови 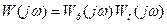 і знаходяться такі параметри настроювань регулятора, при яких ця характеристика торкатиметься кола для заданого значення
і знаходяться такі параметри настроювань регулятора, при яких ця характеристика торкатиметься кола для заданого значення  . При цьому варійованим параметром береться коефіцієнт передачі регулятора
. При цьому варійованим параметром береться коефіцієнт передачі регулятора 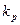 (у разі декількох параметрів настроювання процедура розрахунку залишається такою самою, проте змінюється обсяг обчислень через необхідність визначення найкращого значення
(у разі декількох параметрів настроювання процедура розрахунку залишається такою самою, проте змінюється обсяг обчислень через необхідність визначення найкращого значення 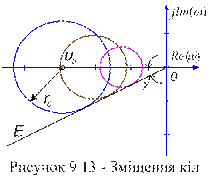
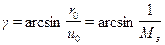 . (9-25)
. (9-25)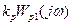 , де
, де 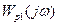 - частотна передаточна функція регулятора при значенні коефіцієнта передачі
- частотна передаточна функція регулятора при значенні коефіцієнта передачі 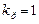 . За заданою передаточною функцією об'єкта управління
. За заданою передаточною функцією об'єкта управління 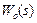 на комплексній площині будується АФЧХ розімкненої системи при одиничному коефіцієнті передачі регулятора і деяких фіксованих значеннях інших настроювань:
на комплексній площині будується АФЧХ розімкненої системи при одиничному коефіцієнті передачі регулятора і деяких фіксованих значеннях інших настроювань: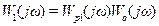 . (9-26)
. (9-26)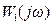 , так і прямої ОЕ.
, так і прямої ОЕ.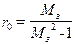 (див. 9-24) до отриманого значення радіуса
(див. 9-24) до отриманого значення радіуса 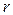 при побудові показує, у скільки разів необхідно змінити коефіцієнт передачі регулятора
при побудові показує, у скільки разів необхідно змінити коефіцієнт передачі регулятора 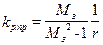 . (9-27)
. (9-27)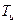 для ПІ-регулятора) визначення
для ПІ-регулятора) визначення 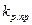 виконується для різних значень
виконується для різних значень 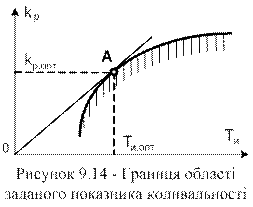 Другий етап. Доведено, що оптимальними по мінімуму середньоквадратичної помилки регулювання настроюваннями (при низькочастотних збуреннях) будуть такі настроювання, при яких система із заданим показником коливальності матиме найбільший коефіцієнт при інтегральній складовій, чому відповідає виконання умови
Другий етап. Доведено, що оптимальними по мінімуму середньоквадратичної помилки регулювання настроюваннями (при низькочастотних збуреннях) будуть такі настроювання, при яких система із заданим показником коливальності матиме найбільший коефіцієнт при інтегральній складовій, чому відповідає виконання умови 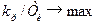 . Ця умова виконується в точці А, в якій пряма з кутовим коефіцієнтом
. Ця умова виконується в точці А, в якій пряма з кутовим коефіцієнтом 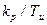 , що виходить з початку координат, торкається до границі області з необхідним запасом стійкості.
, що виходить з початку координат, торкається до границі області з необхідним запасом стійкості.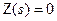 ), управління можна здійснювати за розімкненою схемою (рис. 9.16 а) при передаточній функції регулятора
), управління можна здійснювати за розімкненою схемою (рис. 9.16 а) при передаточній функції регулятора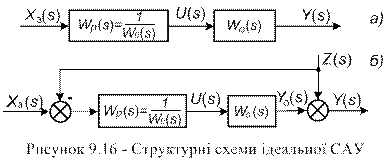
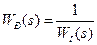 . (9-42)
. (9-42)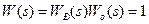 , (9-43)
, (9-43)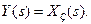 Такий перехідний процес і структуру, що реалізовує його, називають ідеальними.
Такий перехідний процес і структуру, що реалізовує його, називають ідеальними.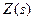 , яке можна виміряти, то теоретично можна синтезувати ідеальну розімкнену САУ (рис. 9.16 б) з повною компенсацією цього збурення, подавши його із зворотним знаком на вхід регулятора з передаточною функцією (9-42). Дійсно, у цьому випадку при
, яке можна виміряти, то теоретично можна синтезувати ідеальну розімкнену САУ (рис. 9.16 б) з повною компенсацією цього збурення, подавши його із зворотним знаком на вхід регулятора з передаточною функцією (9-42). Дійсно, у цьому випадку при 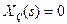 вихідна величина
вихідна величина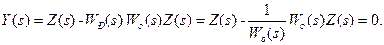 (9-44)
(9-44) на виході об’єкта повністю урівноважуватиме (компенсуватиме) збурення
на виході об’єкта повністю урівноважуватиме (компенсуватиме) збурення 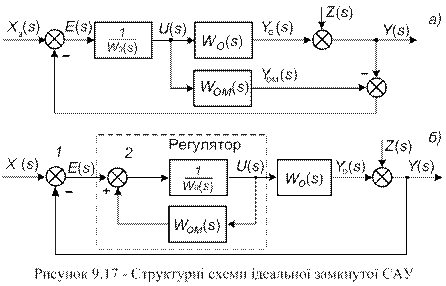
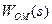 (рис. 9.17 а). Очевидно, що при
(рис. 9.17 а). Очевидно, що при 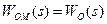 обчислюваний на виході моделі об’єкта сигнал
обчислюваний на виході моделі об’єкта сигнал 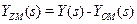 є опосередковано виміряним збуренням
є опосередковано виміряним збуренням 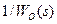 виявиться охопленим внутрішнім додатним зворотним зв’язком, а сигнал після суматора 1 відповідатиме сигналу помилки
виявиться охопленим внутрішнім додатним зворотним зв’язком, а сигнал після суматора 1 відповідатиме сигналу помилки 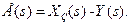 Це означає, що САУ стала замкнутою і працює за принципом від’ємного зворотного зв’язку з регулятором (див. рис. 9.17 б), що має передаточну функцію
Це означає, що САУ стала замкнутою і працює за принципом від’ємного зворотного зв’язку з регулятором (див. рис. 9.17 б), що має передаточну функцію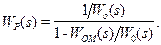 (9-45)
(9-45)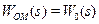 регулятор працюватиме як пропорційний (безінерційний) з коефіцієнтом посилення
регулятор працюватиме як пропорційний (безінерційний) з коефіцієнтом посилення 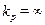 , що відповідає нульовим помилкам за каналами завдання і збурення.
, що відповідає нульовим помилкам за каналами завдання і збурення.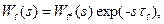 (9-46)
(9-46)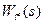 - дробово-раціональна функція, що характеризує інерційну частину об’єкта управління;
- дробово-раціональна функція, що характеризує інерційну частину об’єкта управління; 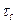 - чисте (транспортне) запізнювання об’єкта управління.
- чисте (транспортне) запізнювання об’єкта управління.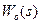 з виразу (9-46) у формулу (9-45), отримаємо передаточну функцію ідеального регулятора для інерційних об’єктів управління із запізнюванням:
з виразу (9-46) у формулу (9-45), отримаємо передаточну функцію ідеального регулятора для інерційних об’єктів управління із запізнюванням: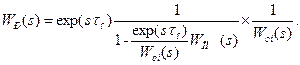 (9-47)
(9-47)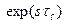 , який відповідає ідеальному упереджувачу (без мінуса), точна реалізація якого технічно неможлива. Для спрощення структури регулятора і полегшення його технічної реалізації робиться припущення, що для об’єктів управління з чистим запізнюванням
, який відповідає ідеальному упереджувачу (без мінуса), точна реалізація якого технічно неможлива. Для спрощення структури регулятора і полегшення його технічної реалізації робиться припущення, що для об’єктів управління з чистим запізнюванням 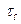 ідеальна САУ відтворює завдання не безінерційно, а із запізнюванням
ідеальна САУ відтворює завдання не безінерційно, а із запізнюванням 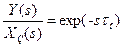 . З іншого боку, відповідно до правила (5-8) структурних перетворень для типової одноконтурної САУ (рис. 5.5) справедливо
. З іншого боку, відповідно до правила (5-8) структурних перетворень для типової одноконтурної САУ (рис. 5.5) справедливо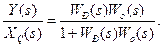 (9-48)
(9-48)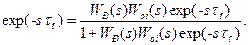 (9-49)
(9-49)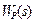 , знаходимо передаточну функцію ідеального регулятора (регулятора Ресвіка):
, знаходимо передаточну функцію ідеального регулятора (регулятора Ресвіка):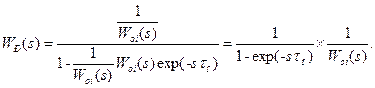 (9-50)
(9-50)



