
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Синтез системи управління за мінімумом інтегральної оцінки якостіСодержание книги
Поиск на нашем сайте
Інтегральні оцінки (критерії) якості перехідних процесів (див. лекцію 12, п. 7.3) дозволяють судити про якість управління шляхом обчислення інтегралів від деяких функцій керованої величини. Ця функція вибирається так, щоб значення певного інтеграла від цієї функції за часом було однозначно пов'язане з якістю перехідного процесу. Як було показано, найбільш доцільним є використання квадратичної оцінки виду
де При синтезі САУ по мінімуму інтегральної оцінки якості структура системи (об'єкта управління і регулятора) вважається відомою і необхідно визначити один або декілька параметрів настроювань коригуючого пристрою. Постановка задачі при цьому зводиться до відшукування таких значень настроювань, які забезпечують мінімум вибраної інтегральної оцінки якості. Найчастіше використовують квадратичну або покращану квадратичну інтегральну оцінку перехідної характеристики стосовно сигналу завдання в системах стеження і відносно сигналу збурення у системах стабілізації. Розглянемо основні етапи розрахунку на прикладі системи управління з одним параметром настроювання регулятора α: 1. Вибираємо вид інтегральної оцінки якості перехідного процесу. Мінімізація квадратичної інтегральної оцінки J 20 виду (9-28) наближає перехідну характеристику до ступінчастої, але при цьому можлива поява значного перерегулювання. Проте якщо в чисельнику передаточної функції замкнутої системи наявні похідні, то значного перерегулювання очікувати не слід. При використанні покращаної квадратичної інтегральної оцінки J 21 (див. п.7.3)
перехідна характеристика наближається до експоненти, і чим більше Θ, тим меншим буде можливе перерегулювання. При підвищених вимогах до форми перехідних характеристик застосовуються покращані інтегральні оцінки ще більш складнішого виду. 2. Складаємо вираз для вибраної інтегральної оцінки. Пряме диференціювання виразів виду (9-28) і (9-29) за параметром α становить істотну трудність, тому для розрахунку квадратичного інтегрального критерію отримано ряд спрощених методів. Так, А. А. Красовським були отримані формули [35], що зв'язують квадратичну інтегральну оцінку з коефіцієнтами передаточної функції замкнутої системи
де m < n, в наступному вигляді
Тут D - визначник Гурвіца, складений за певними правилами; D0, D1, …, Dm - визначники, отримані з D за певними правилами; В0, В1, …, Вm - коефіцієнти, що обчислюються за формулами. В цьому випадку квадратична інтегральна оцінка замінюється на алгебраїчний вираз, залежний від коефіцієнтів (9.30), у тому числі і від α. Для m = n - 1 і n< 10складені таблиці готових виразів для J20. Метод Красовського може бути використаний і для випадку узагальнених (покращаних) квадратичних оцінок [6], які приводяться до вигляду
де Квадратичну інтегральну оцінку якості J 20 можна розрахувати за заданою частотною передаточною функцією замкнутої системи
отриману на основі теореми згортання з використанням перетворень Фур'є. 3. У вираз інтегральної оцінки підставляються відомі параметри системи, після чого вона стає функцією тільки одного невідомого параметра - J 20(α). 4. Диференціюємо вираз інтегральної оцінки за невідомим параметром α і, прирівнявши отриманий вираз до нуля: Може виявитися, що функція J (α) не має мінімуму за α взагалі або усередині області допустимих значень. У такому разі визначають граничні значення α і за знайдений беруть те, що відповідає меншому значенню J (α). 5. Перевіряємо стійкість системи і визначаємо показники якості перехідного процесу при знайденому значенні α опт. При незадовільних показниках якості необхідно шукати інше значення α, змінюючи вид квадратичної оцінки або значення вагових коефіцієнтів. За наявності декількох параметрів настроювання α 1, α 2, … порядок розрахунків залишається тим самим, тільки після визначення інтегральної оцінки як функції невідомих параметрів обчислюють і прирівнюють до нуля її часткові похідні щодо кожного з цих параметрів. Загальним недоліком цього методу є громіздкість і обмеженість застосування переважно для систем, які можна представити передаточними функціями у вигляді відношення двох поліномів невисокого порядку. Наявність сучасних засобів обчислювальної техніки і математичних пакетів, що реалізують числові методи, дозволяє розв’язувати цю задачу прямими пошуковими методами.
Питання для самоконтролю і підготовки до тестового контролю 1. Наближення якої характеристики до ідеальної або еталонної лежить в основі методу Ротача? 2. Як поводиться ідеальна АЧХ стосовно збурювальних і управляючих сигналів? 3. Що береться як критерій настроювання в методі Ротача? 4. Як веде себе показник ступеня згасання перехідного процесу, якщо запас стійкості системи збільшується? 5. Що можна сказати про показник ступеня згасання перехідного процесу, якщо величина резонансного піка модуля АФЧХ збільшується? 6. Мірою чого може бути величина резонансного піку модуля АФЧХ? 7. Показник коливальності М є геометричним місцем з однаковим …? Чим? 8. Чим визначається «заборонена» область на площині АФЧХ, що обмежує величину резонансного піка модуля АФЧХ замкнутої системи? 9. Запишіть вираз для визначення показника коливальності М через амплітуди частотної характеристики. 10. Чому ми можемо використати показник коливальності М як критерій при виборі налаштувань регулятора? 11. У якому діапазоні (приблизно) повинне знаходитися значення показника коливальності М для прийнятного запасу стійкості? 12. Що визначається на першому етапі синтезу системи за методом Ротача? 13. У чому полягає другий етап синтезу системи за методом Ротача? 14. Який параметр настроювань регулятора варіюється на першому етапі синтезу системи управління за методом Ротача? 15. Метод синтезу САУ за мінімумом інтегральної оцінки є точним, наближеним чи графоаналітичним? 16. З яких міркувань робиться вибір оптимальних настроювань регулятора при використанні інтегральних критеріїв якості? 17. Яку інтегральну оцінку якості найчастіше використовують при синтезі САУ? 18. Який можливий недолік використання квадратичного інтегрального критерію при синтезі САУ? 19. Використання покращаної квадратичної інтегральної оцінки наближає перехідну характеристику до …? До чого? 20. У чому основна технічна трудність використання квадратичного інтегрального критерію при синтезі САУ? 21. Якщо вже отримано вираз для інтегрального критерію як функція невідомих параметрів, що необхідно зробити далі? 22. Що потрібно зробити, якщо в результаті синтезу за мінімумом інтегрального критерію отримані незадовільні результати? Лекція 19
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 271; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.54.100 (0.006 с.) |

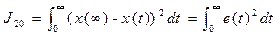 , (9-28)
, (9-28) має смисл функції втрат, або однієї з модифікацій інтегральної оцінки, що враховують швидкість зміни вихідної координати, а іноді і величину сигналу управління.
має смисл функції втрат, або однієї з модифікацій інтегральної оцінки, що враховують швидкість зміни вихідної координати, а іноді і величину сигналу управління.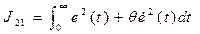 (9-29)
(9-29) , (9-30)
, (9-30) (9-31)
(9-31) , (9-32)
, (9-32) - визначається за формулою для J 20 після знаходження зображення похідної.
- визначається за формулою для J 20 після знаходження зображення похідної. [35], використовуючи відому формулу Релея (Парсеваля)
[35], використовуючи відому формулу Релея (Парсеваля) (9-33)
(9-33)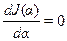 , знаходимо оптимальне значення α опт. Щоб переконатися, що знайдене значення (чи кілька значень) α опт дійсно відповідають мінімуму функції J (α), необхідно виконати додаткову перевірку, наприклад, встановленням факту позитивності другої похідної функції J (α опт) при знайденому значенні параметра. Іноді для такої перевірки зручніше обчислити J (α)при α опт і двох сусідніх значеннях - більшому і меншому, причому за наявності мінімуму останні мають бути більшими за перший.
, знаходимо оптимальне значення α опт. Щоб переконатися, що знайдене значення (чи кілька значень) α опт дійсно відповідають мінімуму функції J (α), необхідно виконати додаткову перевірку, наприклад, встановленням факту позитивності другої похідної функції J (α опт) при знайденому значенні параметра. Іноді для такої перевірки зручніше обчислити J (α)при α опт і двох сусідніх значеннях - більшому і меншому, причому за наявності мінімуму останні мають бути більшими за перший.


