
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Старокостянтинівський районний методичний кабінетСодержание книги
Поиск на нашем сайте Старокостянтинівський районний методичний кабінет Остапчук Н.М. ДИДАКТИЧНІ МАТЕРІАЛИ З МАТЕМАТИКИ Для учнів Го класу М. Старокостянтинів Автор-упорядник: Остапчук Наталія Миколаївна, вчитель математики Решнівецької загальноосвітньої школи І-ІІ ступенів Старокостянтинівської районної ради Хмельницької області...
Рецензент: Сукманюк Світлана Іванівна, методист Старокостянтинівського районного методичного кабінету відділу освіти Старокостянтинівської районної державної адміністрації.
Схвалено на засіданні ради районного методичного кабінету відділу освіти Старокостянтинівської районної державної адміністрації (протокол № від 2011 р.)
У збірнику подано завдання для проведення поточного та тематичного контролю знань учнів 5-х класів із математики. Збірник складений відповідно до діючої програми з метою перевірки засвоєння учнями вивченого матеріалу. Кожну самостійну та контрольну роботу розроблено у двох варіантах. Посібник призначений для вчителів математики та учнів 5-х класів.
Остапчук Н.М. Дидактичні матеріали з математики. 5-й клас Передмова.
У запропонованому посібнику подано дидактичні матеріали для проведення перевірки знань учнями теоретичного матеріалу згідно діючої програми. В даному посібнику запропоновано завдання для проведення самостійних та контрольних робіт з математики для учнів 5-х класів. Кожна робота розроблена у двох варіантах Впродовж вивчення кожної теми передбачається проведення самостійних робіт, мета яких – визначити рівень засвоєння матеріалу теми і вчасно заповнити прогалини в знаннях учнів.
Календарно-тематичне планування (4 год на тиждень, у І семестрі, - 64 год, у ІІ семестрі – 76 год, усього – 140 год)
Варіант 1 1.Записати цифрами числа: а) десять мільярдів вісімдесят тисяч п’ять; б) чотириста п’ятдесят мільйонів п’ятдесят. 2. Запишіть число, у якого: а) 1 сотня 2 десятки 3 одиниці; б) 9 сотень 7 десятків; в) 2 тисячі 3 сотні 1 десяток. 3. Округліть число 12 475 836: а) до десятків; б) до тисяч; в) мільйонів. 4. Дано три числа: 359; 4 327;804. Обчислити: а) суму цих чисел і округлити результат до сотень; б) суму округлених до сотень чисел. 5*. Запишіть усі трицифрові числа, у яких число одиниць у 2 рази більше від числа десятків, а число сотень більше від числа одиниць на 1
Варіант 2 1.Записати цифрами числа: а) вісімдесят вісім мільярдів п’ятдесят три тисячі; б) дев’ятсот дев’яносто три мільйони двадцять. 2. Запишіть число, у якого: а) 8 сотень 3 десятки 4 одиниці; б) 4 сотні 5 одиниць; в) 5 тисяч 1 сотня 4 одиниці. 3. Округліть число 82 436 975: а) до десятків; б) до тисяч; в) мільйонів. 4. Дано три числа: 35; 789; 4 932. Обчислити: а) суму цих чисел і округлити результат до десятків; б) суму округлених до десятків чисел. 5*. Запишіть усі трицифрові числа, у яких число сотень у 3 рази менше від числа десятків, а число одиниць менше від числа десятків на 1.
Варіант 1 1. Як називається результат дії додавання? 2. Як називається компонент дії віднімання, який стоїть на першому місці? 3. Виконайте дії: а) 32 749 + 780 664; б) 286 325 – 96 162. 4. Обчисліть на скільки число 59 428: а) більше від 54 609; б) менше від 79 529. 5. Обчисліть зручним способом: а) 274 + 1 537 + 463; б) 756 – (356 + 235). 6. В овочесховищі було 313 т картоплі. У понеділок привезли на 176 т більше, ніж було в овочесховищі, а у вівторок – на 43 т менше, ніж привезли в понеділок. Скільки тонн картоплі стало в овочесховищі? Варіант 2 1. Як називається результат дії віднімання? 2. Як називається компонент дії віднімання, який стоїть на другому місці? 3. Виконайте дії: а) 499 654 + 80 261; б) 178 214 – 94 153. 4. Обчисліть на скільки число 48 234: а) більше від 42 627; б) менше від 58 974. 5. Обчисліть зручним способом: а) 241 + 2 427 + 373; б) (654 + 289) – 454. 6. До будівельного майданчику привезли 340 т щебеню, що на 81 т більше, ніж піску, і на 103 т менше, ніж цементу. Скільки всього привезли будівельних матеріалів?
Варіант 1 1. Виконайте дії: а) 588 761 + 40 319; б) 954 749 – 87 124. 2. Не використовуючи калькулятора, обчисліть, обираючи зручний порядок дій: а) (1 873 + 1 227) – 873; б) 641 – (141 – 98); в) (797 + 512) – 112; г) 5 124 + 676 + 4 876. 3. На залізничну станцію прийшов поїзд із 97 товарних вагонів. Після того, як частину вагонів відчепили, залишилося 48 вагонів. Скільки вагонів відчепили? 4*. У трьох п’ятих класах 100 учнів. У 5-А і 5-Б 65 учнів, а в 5-А і 5-В – 66. Скільки учнів у кожному класі?
Варіант 2 1. Виконайте дії: а) 724 564 + 90 737; б) 843 524 – 29 846. 2. Не використовуючи калькулятора, обчисліть, обираючи зручний порядок дій: а) (7 122 + 678) – 122; б) 993 – (693 – 108); в) (129 + 741) – 441; г) 1 271 + 549 + 2 729. 3. На складі зберігалося 127 ящиків із фруктами. Після того як привезли ще партію ящиків із фруктами, на складі всього стало 173 ящики. Скільки ящиків із фруктами привезли на склад? 4*. За три дні було скошено траву на лузі площею 35 га. За перший і другий день було скошено траву на площі 22 га. А за другий і третій – на площі 25 га. Скільки гектарів лугу скошували кожного дня?
Варіант 1 1.Подайте: а) 4 м 5 см у сантиметрах; б) 4 023 м у кілометрах і метрах. 2. Знайдіть значення виразу 7 420: х + 29, якщо х = 7. 3. Поїзд ішов 3 год. зі швидкістю V км/год. Який шлях пройшов поїзд? Обчисліть шлях, пройдений поїздом, якщо V = 18. 4. У залі для глядачів кінотеатру в кожному ряді р місць, а кількість рядів на 2 менша, ніж кількість місць у ряді. Скільки всього місць у залі для глядачів? 5*. Складіть вираз для розв’язування задачі. Купили 2 коробки шоколадних цукерок і 3 коробки карамельок. У кожній коробці 20 шоколадних цукерок, а карамельок на k штук більше. Скільки цукерок в усіх коробках?
Варіант 2 1.Подайте: а) 5 км 32 м у метрах; б) 702 дм у метрах і дециметрах. 2. Знайдіть значення виразу 581 – (202 + k), якщо k = 7. 3. Який шлях пройшов поїзд за 6 год, якщо він ішов зі швидкістю т км/год? Обчисліть шлях, пройдений поїздом, якщо т = 60. 4. На ділянці посадили k рядів розсади капусти. Кількість рослин у кожному ряді на 5 більша, ніж кількість рядів. Скільки всього розсади капусти посадили на ділянці? 5*. Складіть вираз для розв’язування задачі. У саду зібрали 5 ящиків яблук і 3 кошики груш. У кожному ящику т кг яблук, а в кожному кошику груш на 3 кг менше, ніж яблук у ящику. Скільки всього зібрали фруктів?
Варіант 1 1. Порівняйте числа, результат порівняння запишіть за допомогою знака «<» або «>»: а) 3 000 080 і 3 000 100; б) 75 102 і 75 201. 2. Знайдіть значення виразу 140: а + 56, якщо а = 28. 3. Знайдіть натуральні числа, що є розв’язками нерівності 11< х <14. 4. Розв’яжіть рівняння: а) x – 49 = 129; б) (х + 25) – 76 = 34. 5*. Автомобіль проїхав 120 км за 2 години. За скільки годин він проїде s км, якщо їхатиме з тією самою швидкістю? Складіть вираз для розв’язання задачі. Обчисліть його значення, якщо s = 600.
Варіант 2 1. Порівняйте числа, результат порівняння запишіть за допомогою знака «<» або «>»: а) 7 003 802 і 7 003 812; б) 91 123 і 91 103. 2. Знайдіть значення виразу 180: b + 56, якщо b = 12. 3. Знайдіть натуральні числа, що є розв’язками нерівності 10< х <13. 4. Розв’яжіть рівняння: а) x + 29 = 43; б)(х – 49) + 51 = 71. 5*. Тракторист зорав за 3 години 60 а землі. За скільки годин цей тракторист зоре S а землі, якщо продуктивність залишиться тією самою? Складіть вираз для розв’язування задачі. Обчисліть його значення, якщо S = 120.
Варіант 1 1. Запишіть переставний закон множення для довільних чисел х і у. 2. Запишіть розподільний закон множення: відносно дії віднімання для довільних чисел s, t, p. 3. Обчисліть, обираючи зручний порядок дій: а) 4 · 256 · 25; б) 4 · 680 · 25; в) 8 · 100 · 5; г) 34 · 7 + 34 · 93; д) 93 · 25 + 107 · 25; е) 254 · 125 + 254 · 875 4. Спростіть вираз: а) 19p + 21p; б) 41k + 23k + k; в) 29x + 14x – 10x. 5. Розв’яжіть рівняння: а) 28х + 5х = 99; б) (х – 2)(8 – х) = 0.
Варіант 2 1. Запишіть сполучний закон множення для довільних чисел т, п і k. 2. Запишіть розподільний закон множення відносно дії додавання для довільних чисел s, t, p. 3. Обчисліть, обираючи зручний порядок дій: а) 125 · 17 · 8; б) 500 · 129 · 2; в) 40 · 32 · 25; г) 73 · 15 – 15 · 71; д) 125 · 423 + 125 · 377; е) 441 · 16 + 559 · 16. 4. Спростіть вираз: а) 13х + 2х; б) 15у + 24у – 9у; в) 72b – 8b – b. 5. Розв’яжіть рівняння: а) 15х + 10х = 75; б) (х – 3)(7 – х) = 0. Варіант 1 1. Знайдіть значення виразу 4 256: 76 + 48 · 36. 2. Спростіть вираз 218 х – 198 х і знайдіть його значення, якщо х = 24. 3. Розв’яжіть рівняння: 5 z + z – 42 = 18. 4. Знайдіть значення виразу: 156 · 49 +227 · 49 – 283 · 49. 5. Виконайте ділення з остачею: а) 15 740: 33 - результат округліть до десятків; б) 27 973: 872 - результат округліть до сотень.
Варіант 2 1. Знайдіть значення виразу 2 – 3 · 19 – 4690: 70. 2. Спростіть вираз 89 х -49 х і знайдіть його значення, якщо х = 16. 3. Розв’яжіть рівняння 7 m + m – 42 = 38. 4. Знайдіть значення виразу: 239 · 37 – 208 · 37 + 169 · 37. 5. Виконайте ділення з остачею: а) 78 909: 76 - результат округліть до сотень; б) 66 666: 689 - результат округліть до десятків.
Варіант 1 1. Перемножити і результат перевірити діленням: 605 · 38. 2. Виконайте дії: a) 512 · 625 – 126 840: 280; b) 32 + (749 - 29): 15. 3. Розв’яжіть рівняння: a) 531 648: х = 526; b) (х - 56) · 9 = 909. 4. На одній ділянці росте 188 кущів, що у 2 рази більше ніж на другій. Скільки кущів росте на двох ділянках? 5. Від двох причалів, розташованих на відстані 315 км., одночасно на зустріч один одному вийшли два теплоходи. Через 5 годин відстань між ними була 90 км. Швидкість одного теплохода 24 км/год. Знайдіть швидкість другого теплохода.
Варіант 2 1. Виконати ділення і результат перевірити множенням: 2 008 609 · 401. 2. Виконайте дії: a) 29 857: 73 + 574 · 89; b) 32 + (749 - 29): 15. 3. Розв’яжіть рівняння: a) 531 648: х = 526; b) 25 + (400 100 – 379 964): 1. 4. В один магазин завезли 324 ц. картоплі, що в 6 разів більше, ніж у другий. Скільки картоплі завезли в другий магазин? 5. З одного пункту в протилежних напрямках одночасно виїхали мотоцикліст і велосипедист. Швидкість мотоцикліста 45 км/год., велосипедиста 15 км/год. На якій відстані один від одного вони будуть через 2 години. Варіант 1 1. Накреслити відрізки MN і QK так, щоб MN = 5 см 2 мм, QK = 4 см 3 мм. 2. Позначити на числовому промені точки P (4) Q (6) A (9). За одиничний відрізок взяти одну клітинку зошита. 3. Накреслити відрізок завдовжки 8 см. Над одним кінцем відрізка написати число 0, над іншим – 16. поділити відрізок на 4 рівні частини. Позначити на отриманій шкалі числа 3; 7; 9; 14. 4. Дано відрізок АВ завдовжки 16 см. Точка М середина відрізка АВ, точка К – середина відрізка МВ. Знайти довжину відрізка АК.
Варіант 2 1. Накреслити відрізки ХУ і ОА так, щоб ХУ = 8 см 4 мм, АО = 3 см 3 мм. 2. Позначити на числовому промені точки А (4) Х (6) Q (10). За одиничний відрізок взяти одну клітинку зошита. 3. Накреслити відрізок завдовжки 9 см. Над одним кінцем відрізка написати число 0, над іншим – 18. поділити відрізок на 6 рівних частин. Позначити на отриманій шкалі числа 4; 8; 10; 16. 4. Точка М середина відрізка АВ, точка К – середина відрізка МВ. Визначити довжину відрізка АК, якщо ВХ = 3 см.
Варіант 1 1. Побудуйте ламану RQSTX з чотирьох ланок так, щоб довжина ламаної дорівнювала 12 см 8 мм. Запишіть довжину кожної ланки. Виміряйте відстань та порівняйте її з довжиною ламаної; запишіть результат порівняння. 2. Точка А лежить на відрізку MN довжиною 36 см. Знайдіть довжину відрізків MA і AN, якщо відрізок МА у 2 рази довший за відрізок AN. 3. Розгорнутий кут поділений на променем на два кути. Градусна міра одного з них 141°. Знайдіть градусну міру другого кута. 4. Точки А, В, С лежать на одній прямій. Яка з цих точок лежить між двома іншими якщо АВ = 33 мм, АС = 6 см, ВС = 2см 7 мм?
Варіант 2 1. Побудуйте ламану ABCDE з чотирьох ланок так, щоб довжина ламаної дорівнювала 10 см 2 мм. Запишіть довжину кожної ланки. Виміряйте відстань та порівняйте її з довжиною ламаної; запишіть результат порівняння. 2. Точка C лежить на відрізку MN довжиною 24 см. Знайдіть довжину відрізків MC і CN, якщо відрізок МC у 3 рази довший за відрізок CN. 3. Розгорнутий кут поділений на променем на два кути. Градусна міра одного з них 52°. Знайдіть градусну міру другого кута. 4. Точки O, M, K лежать на одній прямій. Яка з цих точок лежить між двома іншими якщо OM = 3 см 6 мм, MK = 9 см, OK = 54 мм? Варіант 1 1. Накресліть довільний трикутник; а) прямокутний: б) рівнобедрений. 2. Визначте вид трикутника за його кутами: а) 34°; 127°; 19°; б) 40°; 50°; 90°. 3. Одна сторона трикутника дорівнює 24 см, друга сторона на 18 см довша за першу, а третя у 2 рази коротша за другу. Знайти периметр трикутника. 4. У п’ятикутнику одна сторона 17 см, друга на 8 см більша, а третя дорівнює
Варіант 2 1. Накресліть довільний трикутник: а) рівнобедрений; б) тупокутний. 2. Визначте вид трикутника за його кутами: а) 45°; 60°; 75°; б) 95°; 85°; 5°. 3. Одна сторона трикутника дорівнює 12 см, друга сторона у три рази довша за першу, а третя на 8 см коротша за другу. Знайти периметр трикутника. 4. У чотирикутнику одна сторона дорівнює 20 см, друга у 2 рази менша, а третя становить
Варіант 1 1. Виразіть; а) в квадратних метрах: 3 га 41 а; б) в міліметрах. 1 см2; в) в кубічних сантиметрах: 8 м3. 2. Довжина прямокутника 244 дм, ширина 150 дм. Знайти площу прямокутника і виразити її у квадратних метрах. 3. Ширина прямокутного паралелепіпеда дорівнює 18 см, довжина на 6 см більша, а висота – у два рази менша від довжини. Обчислити об’єм паралелепіпеда. 4. Висота проведена до основи трикутника, дорівнює 6 см і менша за цю основу в 6 разів. Обчислити площу трикутника.
Варіант 2 1. Виразіть; а) в квадратних метрах: 5 км2 42 га; б) в міліметрах: 2 дм2; в) в кубічних сантиметрах: 4 дм3. 2. Довжина прямокутника 40 см, ширина 15 см. Знайти площу прямокутника і виразити її у квадратних дециметрах. 3. Висота прямокутного паралелепіпеда дорівнює 8 см, що на 5 см менше, ніж довжина і у два рази більше, ніж ширина. Обчислити об’єм паралелепіпеда. 4. Основа трикутника дорівнює 34 см і вона на 12 см більша за висоту, проведену до неї. Обчислити площу трикутника.
Варіант 1 1. Накресліть квадрат зі стороною 3 см 2 мм. Знайдіть його периметр і площу. 2. Накресліть прямокутник, довжина якого 4 см, а ширина у 2 рази менша за довжину. Обчисліть периметр і площу прямокутника. 3. Ребро куба дорівнює 5 м. Знайдіть об’єм куба. 4. Довжина прямокутного паралелепіпеда 8 дм. Ширина в 4 рази менша за довжину, а об’єм дорівнює 160 дм3. Знайдіть висоту. 5. Дано три прямокутники, сторони яких відповідно дорівнюють 5 см і 3 см; 5 см і 4 см; 7 см і 2 см. Чи можна скласти квадрат із цих прямокутників? Якщо так, то знайдіть його периметр і площу. Виконайте рисунок. Варіант 2 1. Накресліть квадрат зі стороною 2 см 7 мм. Знайдіть його периметр і площу. 2. Накресліть прямокутник, ширина якого 2 см, а довжина у 3 рази більша від ширини. Обчисліть периметр і площу прямокутника. 3. Ребро куба дорівнює 7 м. Знайдіть об’єм куба. 4. Об’єм прямокутного паралелепіпеда 480 м3. Ширина - 4 м, довжина у два рази більша від ширини.. Знайдіть висоту. 5. Ящик має форму прямокутного паралелепіпеда з вимірами 24 см, 32 см і 40 см. Його заповнили кубиками з ребром 4 см. Скільки кубиків у ящику?
Варіант 1 1. Розмістіть дроби в порядку їх зростання:
2. Допишіть пропущенні чисельники чи знаменники дробів у такі нерівності: а) б) в) 3. Тетянка зібрала 28 грибів, з них 4. Петрик, Олег і Сашко зібрали 70 горіхів. Петрик зібрав
Варіант 2 1. Розмістіть дроби в порядку їх спадання:
2. Допишіть пропущенні чисельники чи знаменники дробів у такі нерівності: а) б) в) 3. Петрик піймав 6 окунів, що становить 4. Наталка, Світлана та Юля збирали рослини для гербарію. Разом дівчатка зібрали 450 експонатів. Наталка зібрала
З однаковими знаменниками»
Варіант 1 1. Виконайте дії: а) б) в) г) д) 2. Розв’яжіть рівняння:
3. Дід Панас продав 240 кг. Картоплі. Першого дня було продано
Варіант 2 1. Виконайте дії: а) б) в) г) д) 2. Розв’яжіть рівняння:
3. За перший місяць побудували
Варіант 1 1. Виділіть цілу частину із неправильного дробу:
2. Виконайте дії: а) б) в) г) 3. Розв’яжіть рівняння: а) б) в) 4. Кролик з’їдає на день 48 г зерна. Це становить 5. Турист пройшов 20 км;
Варіант 2 1. Виділіть цілу частину із неправильного дробу:
2. Виконайте дії: а) б) в) г) 3. Розв’яжіть рівняння: а) б) в)
4. Іванко прочитав 5. Швидкість польоту стрижа 100 км/год. Швидкість
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 635; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.013 с.) |

 суми першої і другої. Обчислити периметр цього п’ятикутника, якщо четверта сторона дорівнює п’ятій і на 5 см менша за другу.
суми першої і другої. Обчислити периметр цього п’ятикутника, якщо четверта сторона дорівнює п’ятій і на 5 см менша за другу. суми першої і другої. Обчислити периметр чотирикутника, якщо четверта сторона дорівнює третій.
суми першої і другої. Обчислити периметр чотирикутника, якщо четверта сторона дорівнює третій. ;
; ;
; ;
; .
. грибів були білі. Скільки білих грибів зібрала Тетянка?
грибів були білі. Скільки білих грибів зібрала Тетянка? усіх горіхів, а Сашко -
усіх горіхів, а Сашко -  решти. Скільки горіхів зібрав Олег.
решти. Скільки горіхів зібрав Олег. ;
; ;
; ;
; .
. усієї кількості риби, яку він піймав. Яку кількість риби піймав Петрик?
усієї кількості риби, яку він піймав. Яку кількість риби піймав Петрик? усіх зібраних експонатів, Юля -
усіх зібраних експонатів, Юля -  решти. Скільки експонатів зібрала Світлана?
решти. Скільки експонатів зібрала Світлана? ;
; ;
; ;
; ;
; .
.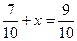 ;
;  ;
;  .
. картоплі, а другого дня -
картоплі, а другого дня - 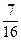 . Скільки кілограмів картоплі було продано за два дні?
. Скільки кілограмів картоплі було продано за два дні? ;
; ;
; ;
; ;
; .
.
 ;
;  .
. дороги, а за другий -
дороги, а за другий -  . Скільки кілометрів дороги було побудовано за два місяці, якщо довжина всієї дороги становить 92 км.
. Скільки кілометрів дороги було побудовано за два місяці, якщо довжина всієї дороги становить 92 км.
 ;
; ;
; ;
; .
. ;
; ;
; .
. маси його денного корму. Скільки кілограмів корму з’їдає кролик на день?
маси його денного корму. Скільки кілограмів корму з’їдає кролик на день? шляху він йшов лісом,
шляху він йшов лісом,  - полем, а решту шляху – уздовж шосе. Скільки кілометрів пройшов турист уздовж шосе.
- полем, а решту шляху – уздовж шосе. Скільки кілометрів пройшов турист уздовж шосе.
 ;
; ;
; ;
;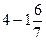 .
. ;
; ;
; .
.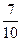 книжки, що становить 56 сторінок. Скільки всього сторінок у книжці?
книжки, що становить 56 сторінок. Скільки всього сторінок у книжці?


