
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамическая модель КШМ. Силы, действующие в кривошипном механизме.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При работе двигателя в КШМ действуют следующие основные силовые факторы: силы давления газов, силы инерции движущихся масс механизма, силы трения и момент полезного сопротивления. При динамическом анализе КШМ силами трения обычно пренебрегают.
Рис. 8.3. Воздействие на элементы КШМ: а — газовых сил; б — силы инерции Рj; в — центробежной силы инерции Кr Силы давления газов. Сила давления газов возникает в результате реализации в цилиндрах рабочего цикла. Эта сила действует на поршень, и ее значение определяется как произведение перепада давления на его площадь: Рг = (рг - р0)Fп (здесь рг — давление в цилиндре двигателя над поршнем; р0 — давление в картере; Fп — площадь поршня). Для оценки динамической нагруженности элементов КШМ важное значение имеет зависимость силы Рг от времени Сила давления газов, действующая на поршень, нагружает подвижные элементы КШМ, передается на коренные опоры картера и уравновешивается внутри двигателя за счет упругой деформации несущих элементов блок-картера силой Силы инерции движущихся масс. КШМ представляет собой систему с распределенными параметрами, элементы которой движутся неравномерно, что приводит к возникновению инерционных нагрузок. Детальный анализ динамики такой системы принципиально возможен, однако сопряжен с большим объемом вычислений. Поэтому в инженерной практике для анализа динамики двигателя используют модели с сосредоточенными параметрами, созданные на основе метода замещающих масс. При этом для любого момента времени должна выполняться динамическая эквивалентность модели и рассматриваемой реальной системы, что обеспечивается равенством их кинетических энергий. Обычно используют модель из двух масс, связанных между собой абсолютно жестким безынерционным элементом (рис. 8.4).
Рис. 8.4. Формирование двухмассовой динамической модели КШМ
Первая замещающая масса mj сосредоточена в точке сопряжения поршня с шатуном и совершает возвратно-поступательное движение с кинематическими параметрами поршня, вторая mr располагается в точке сопряжения шатуна с кривошипом и вращается равномерно с угловой скоростью ω. Детали поршневой группы совершают прямолинейное возвратно-поступательное движение вдоль оси цилиндра. Так как центр масс поршневой группы практически совпадает с осью поршневого пальца, то для определения силы инерции Рjп достаточно знать массу поршневой группы mп, которую можно сосредоточить в данной точке, и ускорение центра масс j, которое равно ускорению поршня: Рjп = - mп j.
Кривошип коленчатого вала совершает равномерное вращательное движение. Конструктивно он состоит из совокупности двух половин коренной шейки, двух щек и шатунной шейки. При равномерном вращении на каждый из указанных элементов кривошипа действует центробежная сила, пропорциональная его массе и центростремительному ускорению. В эквивалентной модели кривошип заменяют массой mк, отстоящей от оси вращения на расстоянии r. Значение массы mк определяют из условия равенства создаваемой ею центробежной силы сумме центробежных сил масс элементов кривошипа: Kк = Krш.ш + 2Krщ или mкrω2 = mш.шrω2 + 2mщρщω2, откуда получим mк = mш.ш + 2mщρщω2/r. Элементы шатунной группы совершают сложное плоскопараллельное движение. В двухмассовой модели КШМ массу шатунной группы mш разделяют на две замещающие массы: mш.п, сосредоточенную на оси поршневого пальца, и mш.к, отнесенную к оси шатунной шейки коленчатого вала. При этом необходимо выполнить следующие условия: 1) сумма масс, сосредоточенных в замещающих точках модели шатуна, должна быть равна массе замещаемого звена КШМ: mш.п + mш.к = mш 2) положение центра масс элемента реального КШМ и замещающего его в модели должно быть неизменным. Тогда mш.п = mш lш.к/lш и mш.к = mш lш.п/lш. Выполнение этих двух условий обеспечивает статическую эквивалентность замещающей системы реальному КШМ; 3) условие динамической эквивалентности замещающей модели обеспечивается при равенстве суммы моментов инерции масс, расположенных в характерных точках модели. Данное условие для двухмассовых моделей шатунов существующих двигателей обычно не выполняется, в расчетах им пренебрегают из-за его малых численных значений. Окончательно объединив массы всех звеньев КШМ в замещающих точках динамической модели КШМ, получим: массу, сосредоточенную на оси пальца и совершающую возвратно-поступательное движение вдоль оси цилиндра, mj = mп + mш.п; массу, расположенную на оси шатунной шейки и совершающую вращательное движение вокруг оси коленчатого вала, mr = mк + mш.к. Для V-образных ДВС с двумя шатунами, расположенными на одной шатунной шейке коленчатого вала, mr = mк + 2mш.к. В соответствии с принятой моделью КШМ первая замещающая масса mj, движущаяся неравномерно с кинематическими параметрами поршня, вызывает силу инерции Рj = - mj j, а вторая масса mr, вращающаяся равномерно с угловой скоростью кривошипа, создает центробежную силу инерции Кr= Кrш + Кк = - mrrω2. Сила инерции Рj уравновешивается реакциями опор, на которые установлен двигатель. Будучи переменной по значению и направлению, она, если не предусмотреть специальных мероприятий, может быть причиной внешней неуравновешенности двигателя (см. рис. 8.3, б). При анализе динамики и особенно уравновешенности двигателя с учетом полученной ранее зависимости ускорения у от угла поворота кривошипа φ силу Рjпредставляют в виде суммы сил инерции первого (РjI) и второго (РjII) порядка:
где С = - mjrω2. Центробежная сила инерции Кr= - mrrω2 от вращающихся масс КШМ представляет собой постоянный по величине вектор, направленный по радиусу кривошипа и вращающийся с постоянной угловой скоростью ω. Сила Кr передается на опоры двигателя, вызывая переменные по величине реакции (см. рис. 8.3, в). Таким образом, сила Кr, как и сила Рj, может являться причиной внешней неуравновешенности ДВС. Суммарные силы и моменты, действующие в механизме. Силы Рг и Рj, имеющие общую точку приложения к системе и единую линию действия, при динамическом анализе КШМ заменяют суммарной силой, являющейся алгебраической суммой: РΣ = Рг + Рj (рис. 8.5, а).
Рис. 8.5. Силы в КШМ: а - расчетная схема; б — зависимость сил в КШМ от угла поворота коленчатого вала
Для анализа действия силы РΣ на элементы КШМ ее раскладывают на две составляющие: S и N. Сила S действует вдоль оси шатуна и вызывает повторно-переменное сжатие-растяжение его элементов. Сила N перпендикулярна оси цилиндра и прижимает поршень к его зеркалу. Действие силы S на сопряжение шатун-кривошип можно оценить, перенеся ее вдоль оси шатуна в точку их шарнирного сочленения (S') и разложив на нормальную силу К, направленную по оси кривошипа, и тангенциальную силу Т.
Силы К и Т воздействуют на коренные опоры коленчатого вала. Для анализа их действия силы переносят в центр коренной опоры (силы К', Т' и Т"). Пара сил Т и Т' на плече r создает крутящий момент Мк, который далее передается на маховик, где совершает полезную работу. Сумма сил К' и T" дает силу S", которая, в свою очередь, раскладывается на две составляющие: N' и Очевидно, что N' = - N и Основные соотношения для рассмотренных сил и моментов имеют следующий вид:
На шатунную шейку кривошипа действуют сила S', направленная по оси шатуна, и центробежная сила Кrш, действующая по радиусу кривошипа. Результирующая сила Rш.ш (рис. 8.5, б), нагружающая шатунную шейку, определяется как векторная сумма этих двух сил. Коренные шейки кривошипа одноцилиндрового двигателя нагружаются силой Использование противовесов приводит к изменению нагруженности коренной шейки.
По дисциплине «силовые агрегаты»
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 906; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.86.30 (0.007 с.) |


 , действующей на головку цилиндра (рис. 8.3, а). Эти силы не передаются на опоры двигателя и не вызывают его неуравновешенности.
, действующей на головку цилиндра (рис. 8.3, а). Эти силы не передаются на опоры двигателя и не вызывают его неуравновешенности.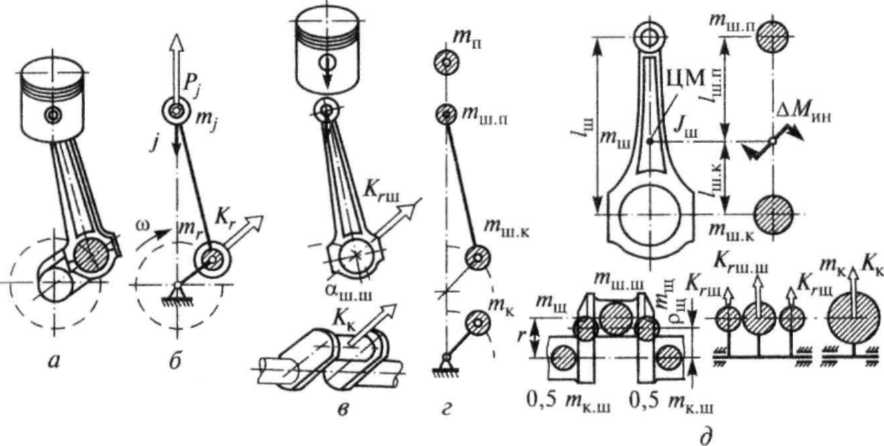


 .
.





 и центробежной силой инерции масс кривошипа
и центробежной силой инерции масс кривошипа  . Их результирующая сила
. Их результирующая сила  , действующая на кривошип, воспринимается двумя коренными опорами. Поэтому сила, действующая на каждую коренную шейку, равна половине результирующей силы
, действующая на кривошип, воспринимается двумя коренными опорами. Поэтому сила, действующая на каждую коренную шейку, равна половине результирующей силы  и направлена в противоположную сторону.
и направлена в противоположную сторону.


