Дробный факторный эксперимент. Выбор полуреплики и четвертьреплики.

При большом числе факторов (k >3) проведение полного факторного эксперимента связано с большим числом, экспериментов, значительно превосходящим число коэффициентов линейной модели. Если при получении модели можно ограничиться, линейным приближением, т. е. получить адекватную модель в виде полинома y = b ₀ + b ₁ x ₁ + b ₂ x ₂+...+ b _k x _k, то число экспериментов можно резко сократить в результате использования дробного факторного эксперимента. Так, например, в полном факторном эксперименте типа 2² при линейном приближении коэффициент регрессии b ₁₂ можно принять равным нулю, а столбец x ₁ x ₂ матрицы (табл. 16.4) использовать для третьего фактора x ₃.

Таблица 16.4

Матрица планирования

 

Номер экспер.	x 0	x 1	x 2	x 3 (x 1 x 2)	y
	+	+	+	+	y 1
	+	-	+	-	y 2
	+	+	-	-	y 3
	+	-	-	+	y 4

 

В этом случае линейная модель будет определяться уравнением y = b ₀ + b ₁ x ₁ + b ₂ x ₂+ b ₃ x ₃. Для определения коэффициентов этого уравнения достаточно провести четыре эксперимента вместо восьми в пол­ном факторном эксперименте типа 2³. План эксперимента, преду­сматривающий реализацию половины экспериментов полного факторного эксперимента, называют полурепликой. При увеличении числа факторов (k >3) возможно применение реплик большей дробности. Дробной репликой называют план эксперимента, являющийся ча­стью плана полного факторного эксперимента. Дробные реплики обозначают зависимостю 2 ^k-p, где p - число линейных эффектов, приравненных к эффектам взаимодействия. При p = 1 получают полуреплику; при p = 2 получают ¼ - реплику; при p = 3 получают ⅛ - реплику и т. д. по степеням двойки.

12. Дробный факторный эксперимент. Достоинства и недостатки. Число степеней свободы, насыщенный план.

Идея дробного факторного эксперимента состоит в том, что один или несколько факторов изменяют в процессе эксперимента так, как изменялось бы произведение нескольких оставшихся факторов в полном факторном эксперименте, т.е. 1 или несколько факторов равны произведению нескольких факторов.

2^к-р – тип дробно-факторного эксперимента, р – число факторов, приравненных к произведению других факторов.

Реплики, в которых число опытов равно числу коэффициентов, называются насыщенными. Выбор дробной реплики зависит от конкретной задачи. Для получения линейной модели рекомендуют выбирать дробные реплики с возможно большей разрешающей способностью, т. е. реплики, у которых линейные эффекты смешаны с эффектами взаимодействия близкими к нулю. При выборе дробной реплики важно учитывать насыщенность плана, т. е. соотношение между числом опытов и числом коэффициентов, определяемых по результатам этих экспериментов. Дробная реплика, полученная заменой всех эффектов взаимодействия новыми факторами, называется насыщенной. Применение насыщенных планов требует минимального числа экспериментов. Число экспериментов в матрице насыщенной дробной реплики равно числу коэффициентов линейной модели. Гипотезу адекватности модели в этом случае проверить невозможно, так как число степеней свободы равно нулю.

«+»ДФЭ позволяет минимизировать число опытов, но при этом

«-»оценки коэффициентов получаются смешанными.

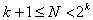Число опытов в дробной реплике должно удовлетворять неравенству , где 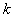— число факторов, для получения несмешанных оценок линейных эффектов.Если 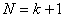, то есть число опытов равно числу определяемых коэффициентов линейной модели, дробная реплика представляет собой насыщенный линейный ортогональный план. Поскольку число опытов в насыщенных планах равно числу определяемых коэффициентов, число степеней свободы дисперсии адекватности 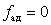. Для поверки адекватности линейной модели, полученной по насыщенному плану, необходим дополнительный эксперимент.

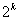Таким образом, оптимальные двухуровневые планы и 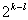имеют следующие преимущества:

· планы ортогональны, и поэтому все вычисления просты, все коэффициенты определяются независимо друг от друга;

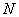· каждый коэффициент определяется по результатам всех опытов;

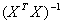· для данного числа опытов эти планы имеют минимальный определитель ковариационной матрицы ; в связи с этим все коэффициенты определяются с одинаковой и минимальной дисперсией, то есть планы обладают свойством Д-оптимальности;

· линейные планы и обладают свойством ротатабельности.